 ネック伝播の振動
ネック伝播の振動
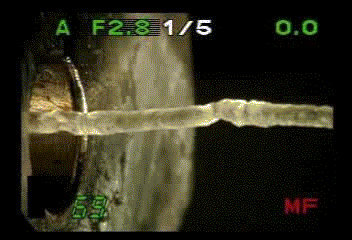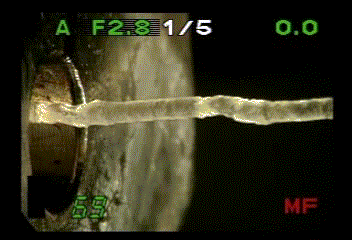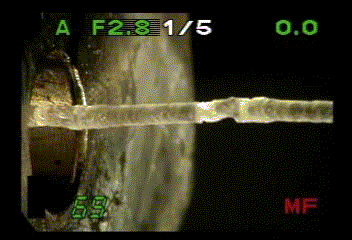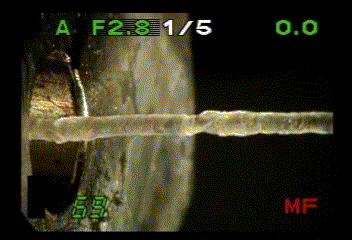 melt fracture
melt fracture
定常状態が不安定になり自励振動が始まる現象は、高分子の成形・加工では非常によく出くわす不安定現象です。私が知っている限りでも、フィルムの冷延伸過程におけるネック伝播の振動[1]、溶融体押しだし過程における melt fracture(融液破断)[2]、繊維の紡糸過程におけるdraw resonance [3] 、ゴム引き裂きの振動 [4]、粘着テープ剥離時のビリビリ[5] などがあります。これらの現象の解明は実用的側面からも非常に重要な、古くからの問題です。これらの系の微視的な変形過程は当然のことながら全く異なるはずですが、変形速度と荷重の関係が見かけ上同様にみえます(例:図1、2)。これらの系はシステムとしての開放性、非線形性、組織性、関係性(中村量空著「複雑性の意匠」より)に共通の特徴があります。そこで私たちは、非線形動力学系での定常安定解のリミットサイクルへの分岐であるとして、これらの現象にアプローチしています。
上記の自励振動におけるダイナミクスの類似点を以下に挙げてみます。
以上の現象は、非線形動力学系でよく見られる特徴であり、定常安定解のリミットサイクルへの分岐という立場に立てば定性的には以下のように説明されます。
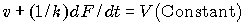
このように自励振動を示す系で特徴的に見られる性質を利用して、個々の物理的機構では、どの過程がダイナミクスを決定し、どれが副次的な現象であるのかを明らかにするというアプローチで研究を進めています。
[参考文献]
[1]G.P. Andriavova, B.A. Arutyunov, Yu.V. Popov: J. Polym. Sci., Polym.Phys. Ed. 16 (1978) 1139.
G.I. Barenblatt: Mech. Solids 5 (1970) 110.
A. Toda: Polymer 34 (1993) 2306.
A. Toda: Polymer 35 (1994) 3638.
A. Toda, C. Tomita, M. Hikosaka, Y. Hibino, H. Miyaji, C. Nonomura, T. Suzuki and H. Ishihara: Polymer, 43 (2002) 947
[2] S. Middleman: in Fundamentals of Polymer Processing, McGraw-Hill,New York, 1977 Chaps. 14 and 15.
K. Sato, A. Toda: J. Phys. Soc. Japan 68 (1999) 77.
K. Sato: Progr. Theor. Phys. in press.
K. Sato and A. Toda: J. Phys. Soc. Japan, 70 (2001) 3268.
[3] Kase, S., "High-Speed Fiber Spinning" Ziabicki, A. and Kawai, H.Edn., John Wiley (1984) p. 67.
[4] R.S. Rivlin, A.G. Thomas: J. Polym. Sci., 18 (1955) 177-188.
[5] 浦濱圭彬: 日東技報 29 (1991) 1 , 高分子 43 (1994) 478.
Y. Yamazaki and A. Toda: J. Phys. Soc. Japan, 71 (2002) 1618