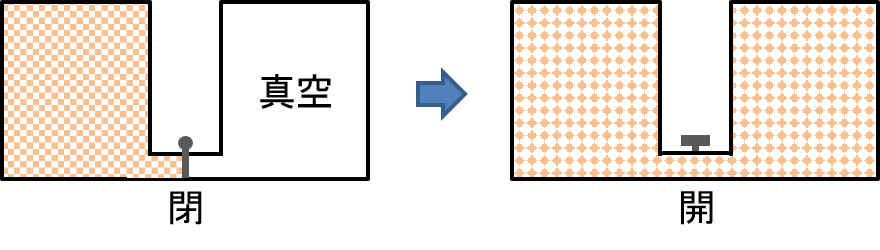
エントロピー増大の原理を前提とすれば,孤立系(ΔU=0)としての断熱自由膨張は,温度変化がない理想気体に限らず,温度変化が生じる実在気体でも,下記の通り不可逆となることが分かる。
また,等温環境下の自由膨張も同様に不可逆である。(下記PDF資料参照)
さらには,同様な断熱下(ΔH=0)の不可逆操作によるジュール-トムソン効果も知られている。(参考1)
これらの過程におけるエントロピー変化量の評価の際には,状態量となるエントロピーの定義に従うと,結果的に同一の状態変化をもたらす,ある経路に沿った可逆過程における変化量として求める必要がある。このとき,当然のことではあるが,仕事を行わない自由膨張の経路とは無関係に,dU=TdS−pdV の表式を用いることができる。
そこで例えば,断熱自由膨張(dU=0)に伴う状態変化に相当する可逆変化の場合には (∂S/∂V)U=p/T>0 となり,膨張時にエントロピーが増大することが分かる。この無限小変化の結果から,有限の変化の場合にも同様に ΔS=∫(p/T)dV>0 となる。すなわち,エントロピー増大の原理により,作業物体の種類によらず断熱自由膨張は不可逆となる。
特に,状態方程式 pV=nRT に従う理想気体では,ΔS=nR∫(1/V)dV=nRln(V2/V1)>0 となる。一方,本文で示されたように、理想気体における一般形は ΔS=∫(CV/T)dT+nRln(V2/V1) と表される。内部エネルギーの変化しない断熱自由膨張において,理想気体では dT=dU/CV=0 となり温度も変化しない。そこで,一般形 ΔS の第1項がゼロとなることから ΔS=nRln(V2/V1)>0 であることを結論してもよい。
以上の考察の大事な点を確認しておくと、状態量となるエントロピーについては,可逆な経路における変化量として ΔS が定義されたことを思い出してほしい。これは,可逆な経路で評価しても構わないということではなく,可逆な経路で評価しなければならないということである。非平衡下の不可逆変化となる自由膨張途中のエントロピー変化を直接評価して ΔS を得るわけでは決してない。なお,変化量 ΔS は可逆・不可逆を問わず経路によらない。これは,熱力学における全ての状態量の特性である。
また、容器に収められていない限り四方八方に散逸してしまうことから,明らかに不可逆となるべき気体の自由膨張においても,確かに ΔS>0 となることが確認できた。気体の自由膨張は,クラウジウス,トムソンの両原理で規定される不可逆過程(温度差伝熱や摩擦熱発生)とは一見無関係に思えるが,その不可逆性は普遍的に成り立つべきエントロピー増大則の対象として確かに包含されている。
温度差下の伝熱,「仕事→熱」サイクル,気体の自由膨張が,熱散逸や物質拡散による不可逆過程の特徴を表す代表的な操作となる。
