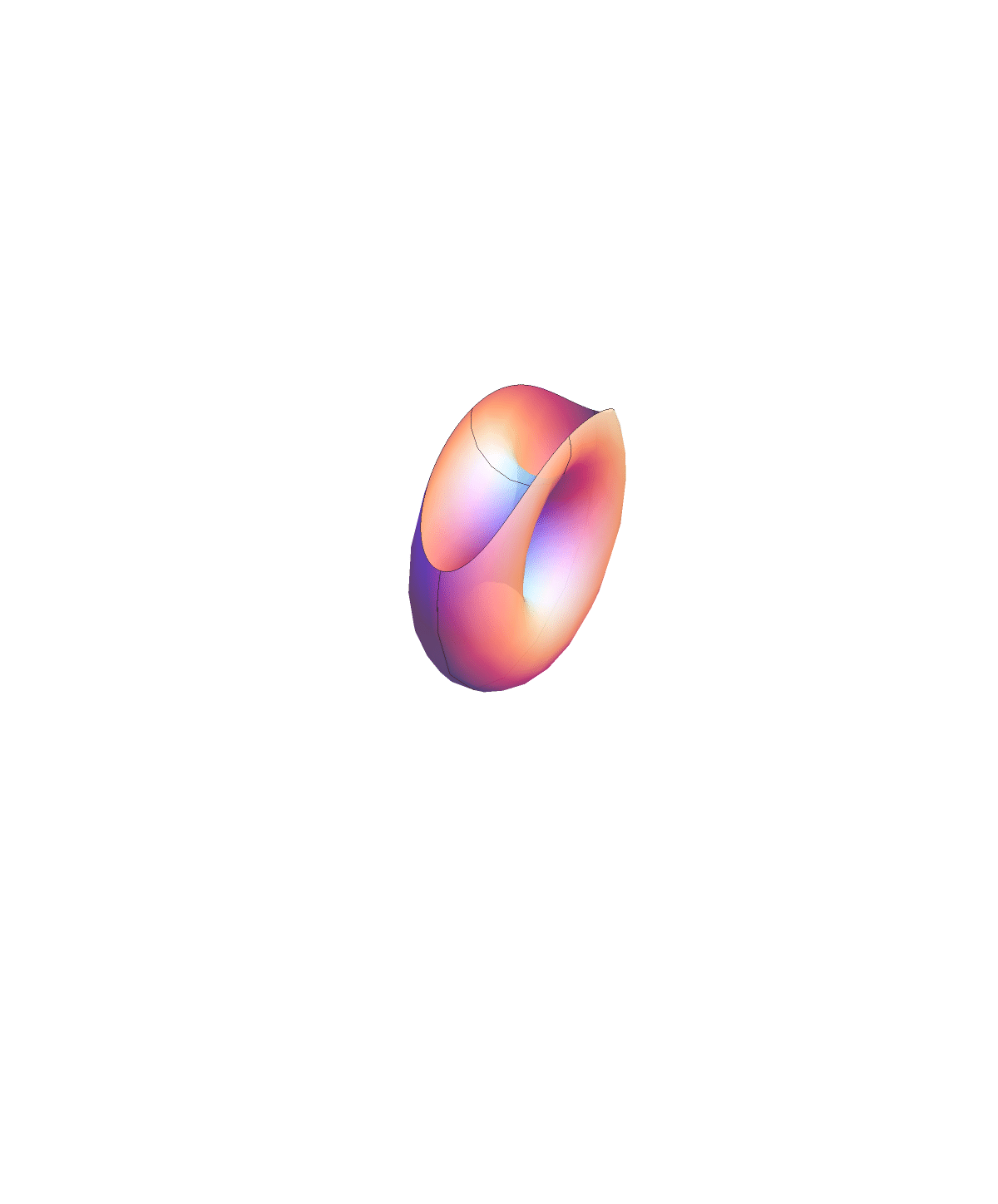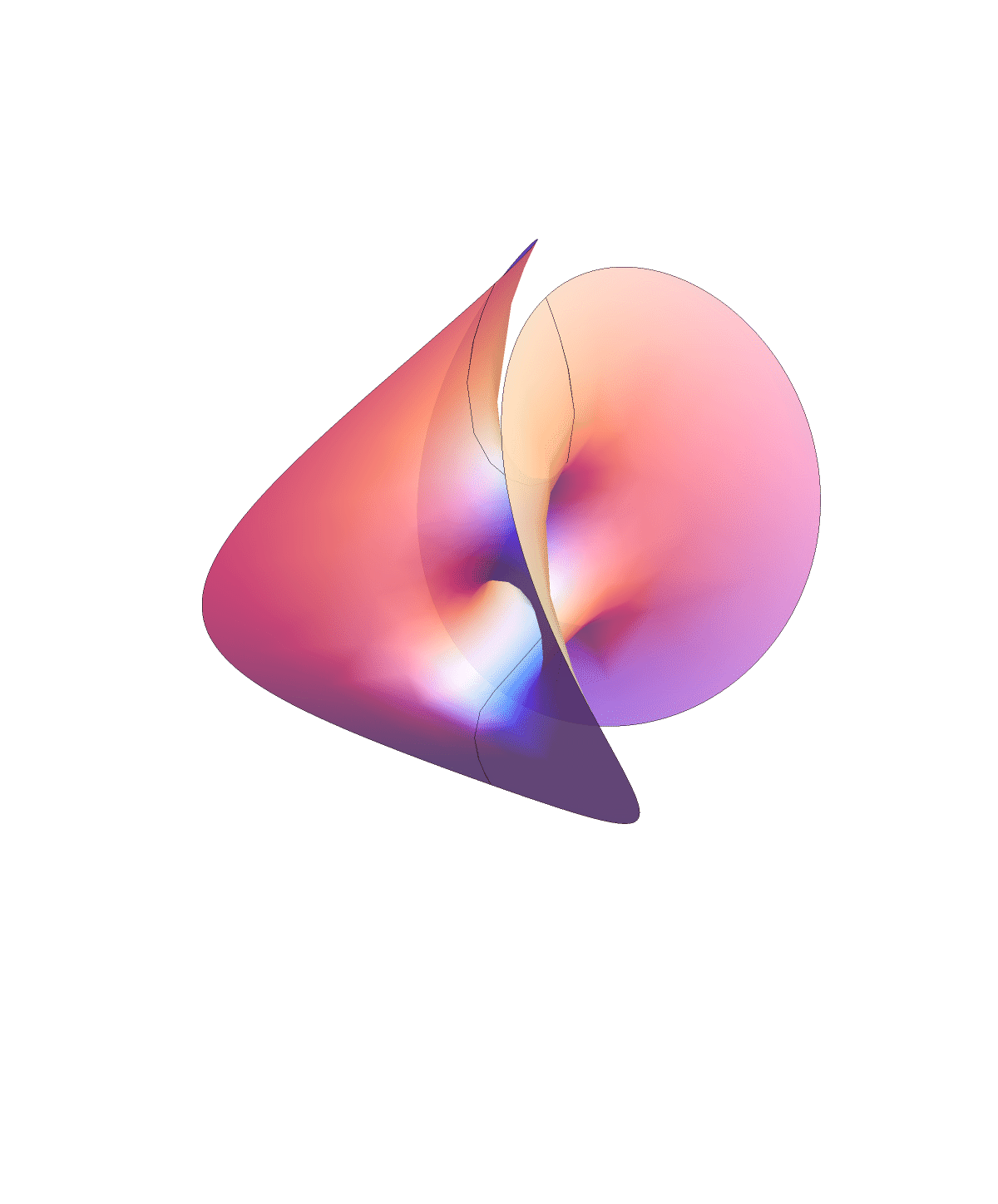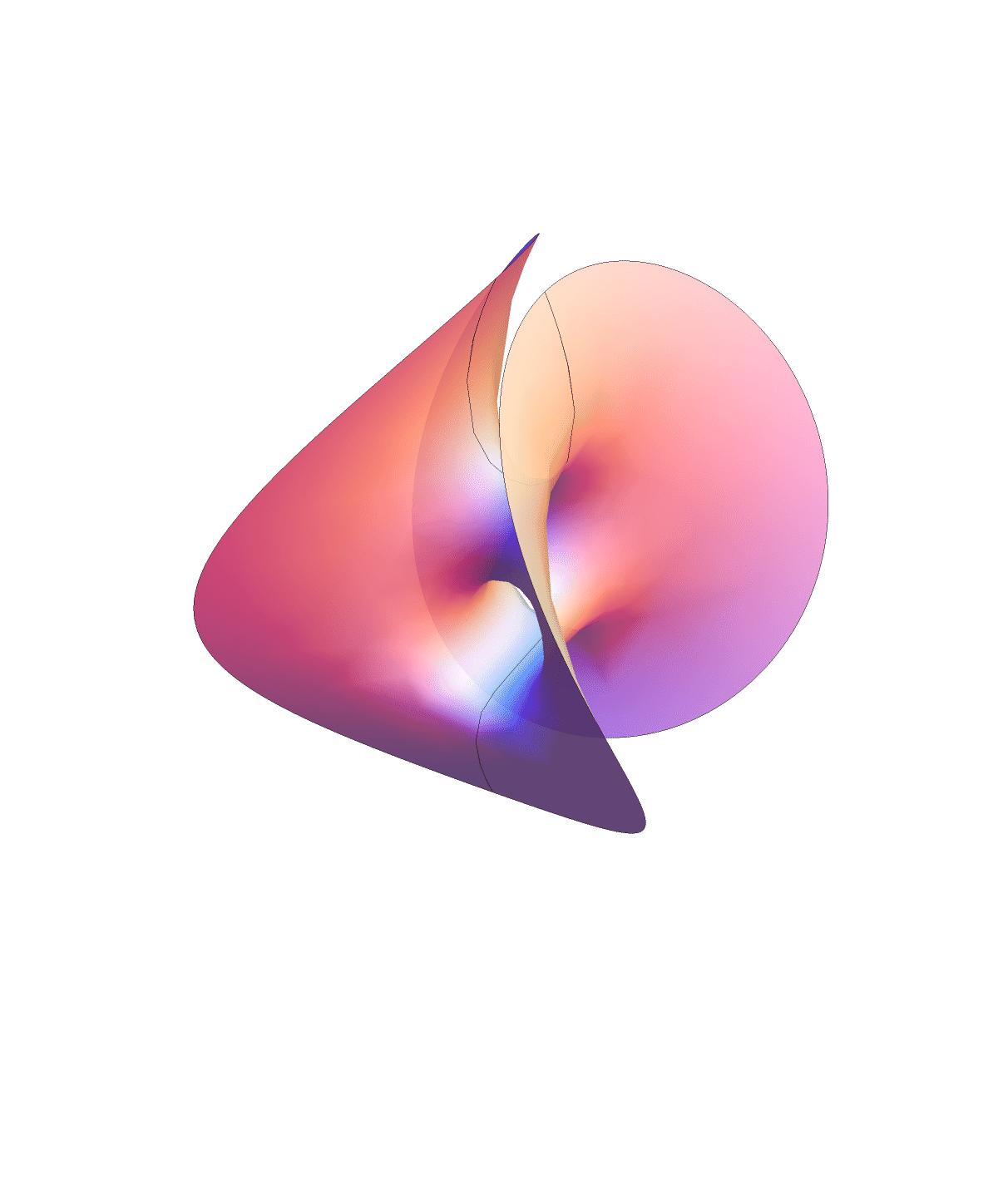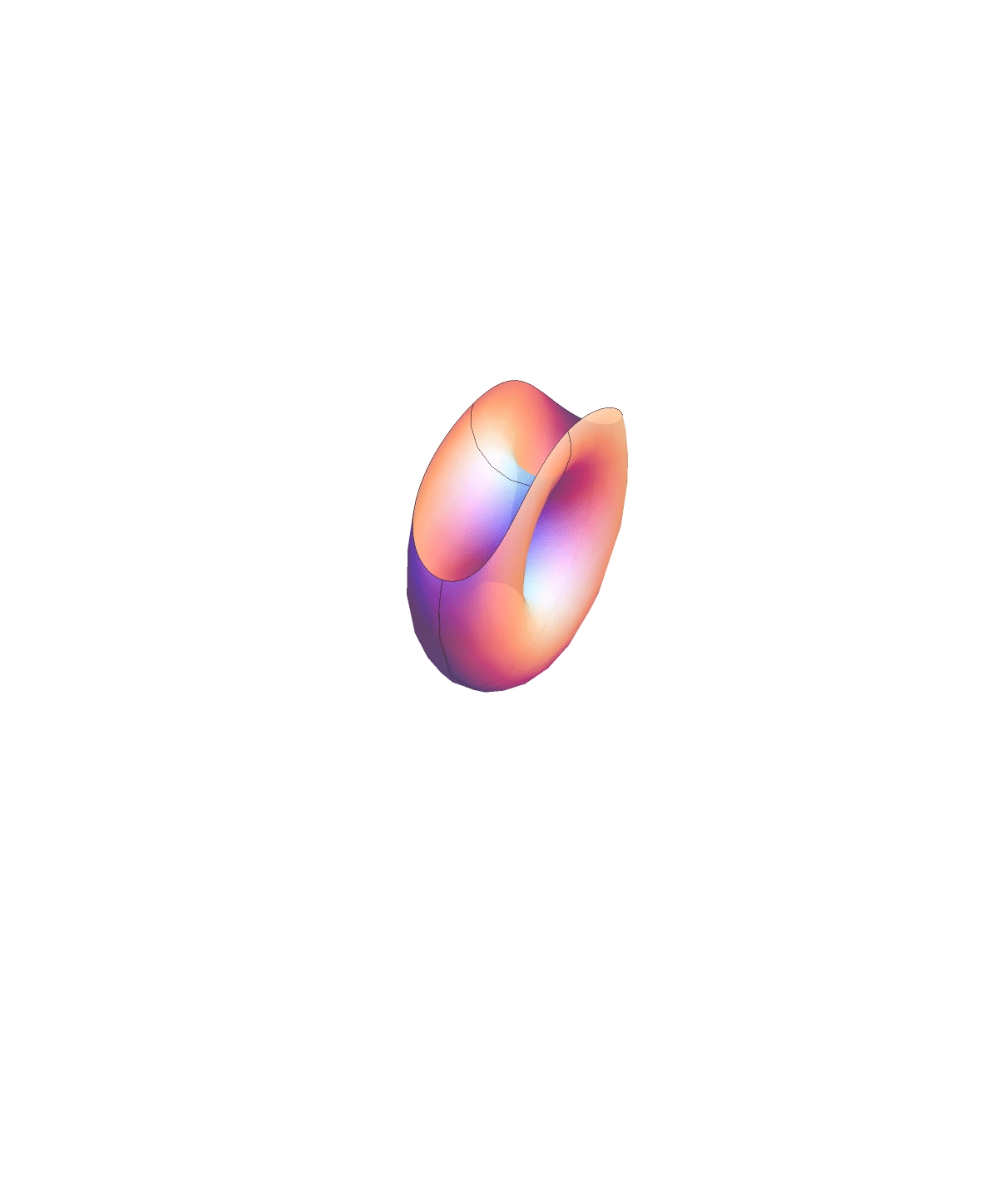Chen-Gackstatter surface family
First constructed by C. C. Chen and F. Gackstatter for $j=1,2$ and $k=1$. Then generalized by N. do Espírito Santo, H. Karcher, E. Thayer, K. Sato, M. Weber and M. Wolf, and so on.
Weierstrass Data
\[ \overline{M}=\left\{(z,w)\in(\mathbb{C}\cup\{\infty\})^2\;;\;w^{k+1}=\frac{z\prod_{1\le m\le j/2}(z^2-a_{2m}^2)}{\prod_{1\le n\le (j+1)/2}(z^2-a_{2n-1}^2)}\right\}, \] where $j$, $k$, $m$, $n$ are positive integers and $a_1,\dots,a_j$ are real such that $1=a_1\lt a_2\lt \cdots\lt a_j$. \[ M=\begin{cases} \overline{M}\setminus\{(\infty ,\infty)\} & \text{(for $j$ even)}, \\ \overline{M}\setminus\{(\infty ,0)\} & \text{(for $j$ odd)}, \end{cases} \] \[ g=cw^k,\qquad \eta = \frac{dz}{w^k}, \] where $c$ is a positive real constant. For given $j$ and $k$, we can choose $a_2,\ldots ,a_j$, and $c$ so that $f$ is single valued on $M$.
Topology
This surface is topologically a compact surface of genus $jk$ with one point removed. The animation below shows the deformation between the surface with $j=k=1$ and the standard torus with a disk removed.