12月8日 演習(レポート)
Mathematicaでの表示結果
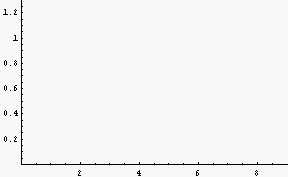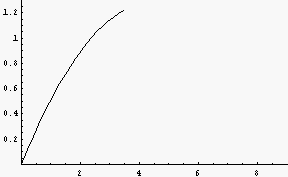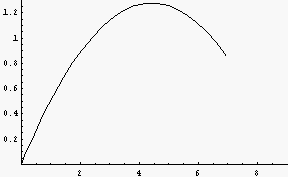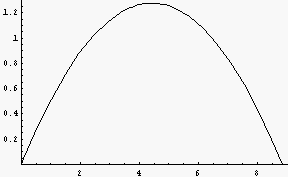
解答例(黒字の部分をコピー&ペーストしてMathematicaで実行可能)
微分方程式のxとyに関する解 x = vt・cos(θ), y = vt・sin(θ)-(g/2)t^2 を入力しない方法。
m = 5;
v = 10;
st = Pi/6;
g = 9.8;
DSolve[{m*x''[t] == 0, x'[0] == v*Cos[st], x[0] == 0}, x[t], t]
DSolve[{m*y''[t] == -m*g, y'[0] == v*Sin[st], y[0] == 0}, y[t], t]
- S=NDSolve[
- { x''[t] == 0, x'[0] == v*Cos[st], x[0] == 0,
- m*y''[t] == -m g, y'[0] == v*Sin[st], y[0] == 0},
- {x[t],y[t]}, {t,0,1.2}]
<<
Graphics`Animation`
- Animate[
- ParametricPlot[
- Evaluate[{x[t],y[t]}/.S],
- {t,n-0.005,n+0.005},PlotRange->{{0,9},{0,1.3}}
- ],{n,0.01,1.1,0.1}
- ];
"Aida Michiko"と"Hiroshi Yoshimitu"
の解答を組み合わせた例
Animate[
ParametricPlot[
{5*Sqrt[3]*t,(5*t)-(4.9)*t^2},{t,n-0.005,n+0.005},PlotRange->{{0,10},{0,1.3}}
],{n,0.01,1.1,0.1}
];
3D表示への改良例
xp[t_] := 5 Sqrt[3] t;
zp[t_] := 5t - 9.8/2*t^2;
- Animate[
- ParametricPlot3D[
- {xp[t],2.5,zp[t]},{t,t1-0.01,t1+0.01},PlotRange->{{0,9.5},{0,5},{0,2}}
- ],{t1,0.001,1.1,0.1}
];
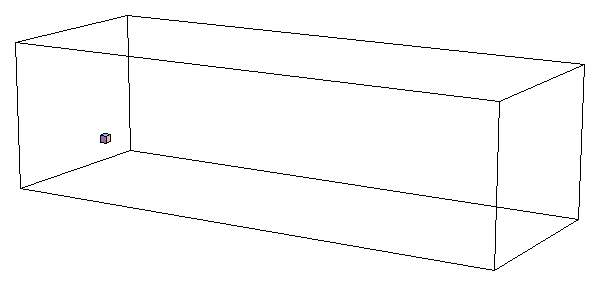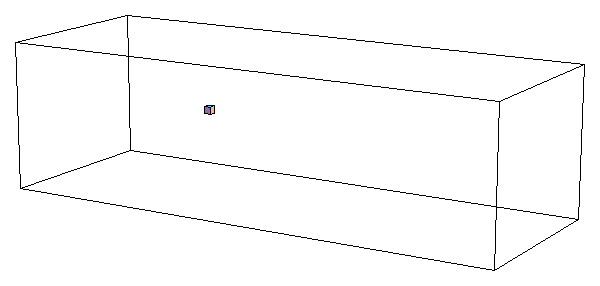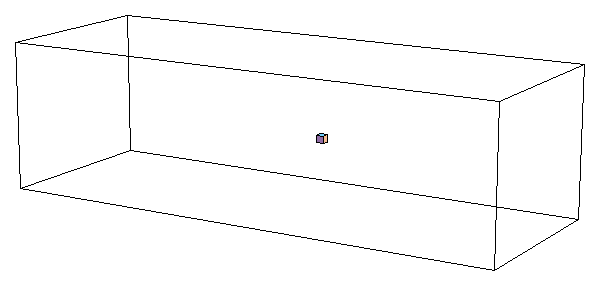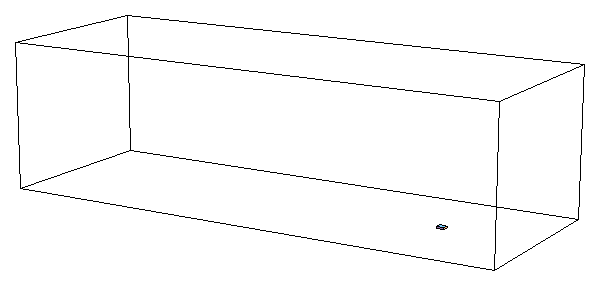
"Table","Show"と"Cuboid"
(まだ教えてない、新コマンド)を
使った「空飛ぶ立方体」(2番目のアニメ)
xp[t_] := 5 Sqrt[3] t
yp[t_] := 5t - 9.8/2*t^2
- Table[
-
- {Show[
- Graphics3D[
- Cuboid[{xp[t]-.1,2.5-.1,yp[t]-.1},{xp[t]+.1,2.5+.1,yp[t]+.1}],
- PlotRange->{{-1,13},{0,5},{-1,3}}
- ],ViewPoint->{1.703,-2.818,0.779}
- ]},{t,0.0,1.2,0.1}
- ];
その他の解答例
1."Table"を使った例(1番目上のアニメ) by michimura shinnji
Also reported by takeharu fujie, Shou Takemitsu, Akazawa Noritoshi, yasuakiterao,
Yoneshima Junko, Wakamoto Shuichi , hirotaka, yu-ji.m, Yasuhiko Mizuno, hashimoto.
m = 5
v = 10
a = Pi/6
g = 9.8
DSolve[{m*x''[t] == 0, x'[0] == v*Cos[a], x[0] == 0}, x[t], t]
DSolve[{m*y''[t] == -m*g, y'[0] == v*Sin[a], y[0] == 0}, y[t], t]
球が地面に戻る時間を計算した例
by takeharu fujie, Yoneshima Junko, Wakamoto Shuichi , yu-ji.m
Solve[5t - 9.8*t^2/2 == 0, t]
ParametricPlot[{x[t] = 5*3^(1/2)*t, y[t] = 5t - 9.8*t^2/2}, {t, 0, 1.02041}];
Table[
ParametricPlot[
{x[t] = 5*3^(1/2)*t, y[t] = 5t - 9.8*t^2/2}, {t, 0, n},
PlotRange -> {{0, 10}, {0, 1.3}}],
{n, 0, 1.1, 0.1}
];
2."Animate"を使った例 by Hiroshi Yoshimitu.
「短い線が飛ぶアニメ」。x[t],y[t]をy[x]に変換。
- Animate[
- Plot[x/(3^(1/2)) - x^2/15, {x, 5*3^(1/2)*t, 5*3^(1/2)*(t + 0.05)}],
- {t,0,1,0.1}, PlotRange->{{0, 10}, {-0.2, 1.3}}];
3."Animate"と"ParametricPlot"を使った例 by Aida Michiko
-
Animate[
- ParametricPlot[
- {5*Sqrt[3]*t,(5*t)-(4.9)*t^2},{t,0,n},PlotRange->{{0,10},{0,1.3}}
- ],{n,0.1,(50/49),0.1}
- ];
4.x[t],y[t]をy[x]に変換 by Takuya Takahash and others.
-
Animate[
- Plot[
- {Tan[Pi/6]*x-4.9*(x^2)/((10^2)*((Cos[Pi/6])^2))},{x,0,10*Cos[Pi/6]*t}
- ],{t,0.0,1.2,0.1},AxesLabel->{"x","y"},PlotRange->{{0,9.5},{0,1.3}}
-
];
5.軌跡を点で表示 by Takuya Takahash
(小さくて見えない?)
Animate[
ParametricPlot[
{10*Cos[Pi/6]*t,10*Sin[Pi/6]*t-4.9*(t^2)},{x,0,10},PlotStyle->PointSize[0.5]
],{t,0,1.2,0.1},AxesLabel->{"x","y"},PlotRange->{{0,9.5},{0,1.4}}
];
ホームページに戻る
Dec. 14 2000


