Last update : May 10, 2009
| 日程 | : | 2009年6月1日(月) |
| 場所 | : | 東京都千代田区外神田1-18-13 |
| 秋葉原ダイビル12階 首都大学東京 | ||
| 「秋葉原サテライトキャンパス会議室AB」 |
| 酒井 高司 | (首都大学東京理工) |
| 田崎 博之 | (筑波大学数理物質) |
| 小野 肇 | (東京理科大学理工) |
| 黒須 早苗 | (東京理科大学理) |
ドイツ・ミュンヘン工科大学のJosef Dorfmeister教授は日本学術振興会外国人招へい研究者(短期)として、2009年4月から2009年6月まで首都大学東京に滞在されています。 今回はDorfmeister教授に彼のDPW法とその応用について入門的な講義をしていただきます。
DPW法とは:
Dorfmeister-Pedit-Wuによって与えられた、可積分系の理論をもとにリーマン面から対称空間へ調和写像を構成する理論です。
現在では平均曲率一定曲面などの研究に広く応用されています。
| 13:30-14:30 | Martin Guest (首都大学東京) |
| Warming up lecture "Introduction to loop groups" | |
| 15:00-16:00 | Josef Dorfmeister (ミュンヘン工科大学) |
| "Introduction to the loop group method of integrable surfaces" | |
| In this talk we will give an introduction to the loop group method for the construction of certain classes of surfaces. The talk addresses a general mathematical audience. Some examples and pictures will illustrate the general theory. | |
| 16:30-17:30 | Josef Dorfmeister (ミュンヘン工科大学) |
| "Constructions of trinoids in R^3 of genus g = 0 with embedded ends" | |
| This talk will show how one can construct surfaces of constant mean curvature in R^3 which have embedded annular ends. Starting from sufaces of revolution we will go on to explain, how one can obtain constant mean curvature immersions from the sphere S^2 minus three puntures to R^3. We will present recent Ph.D. work of Phillip Lang classifying rotationally symmetric trinoids. If time permits we will explain the relation of this theory to hypergeometric functions. |
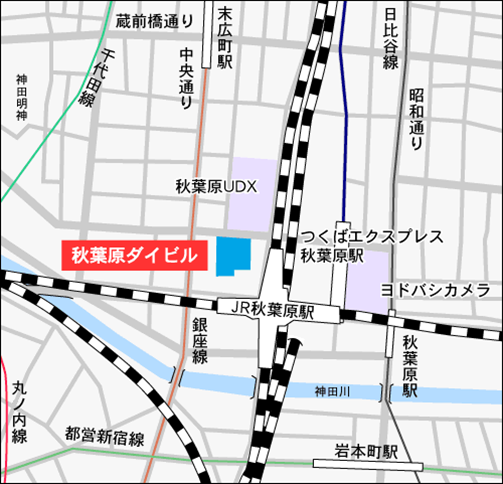
| JR 山手線・京浜東北線・総武中央線 | 「秋葉原駅」 | 徒歩約1分 |
| つくばエクスプレス | 「秋葉原駅」 | 徒歩約2分 |
| 東京メトロ日比谷線 | 「秋葉原駅」 | 徒歩約5分 |
| 東京メトロ日銀座線 | 「末広町駅」 | 徒歩約5分 |
問合せ先: 酒井 高司 sakai-t (at) tmu.ac.jp