Last update : May 30, 2011
第6回 秋葉原微分幾何セミナー
| 日程 |
: |
2011年7月16日(土) |
| 場所 |
: |
東京都千代田区外神田1-18-13 |
|
|
秋葉原ダイビル12階 首都大学東京 |
|
|
「秋葉原サテライトキャンパス会議室DE」 |
| 講演者 |
: |
梅原 雅顕 氏(東京工業大学大学院情報理工学研究科) |
|
|
山田 光太郎 氏(東京工業大学大学院理工学研究科) |
| 講演題目 |
: |
「特異点をもつ曲面の完備性と弱完備性」 |
組織委員:
-
| 酒井 高司 |
(首都大学東京理工) |
| 田崎 博之 |
(筑波大学数理物質) |
| 小野 肇 |
(東京理科大学理工) |
| 黒須 早苗 |
(東京理科大学理) |
概要: ガウス曲率一定曲面あるいは平均曲率一定曲面を考えると,しばしば特異点が自然に現れることがあります.
そのような曲面を大域的に扱うために完備性と弱完備性の定義を与えて,特に関数論的な手法が有効となる曲面のクラスについて,様々な応用を紹介します.
プログラム:
-
| 11:00-12:00 |
|
Osserman の補題と極小曲面(梅原) |
| |
|
古典的な極小曲面論において,完備性と有限全曲率性からWaierstrassデータが,真性特異点を持たないことを示すときの鍵となるのが Osserman の補題です.この補題の役割と証明について解説します. |
| |
|
|
| 13:30-14:30 |
|
時空の極大曲面と特異点の入門(山田) |
| |
|
時空の極大曲面と古典的な極小曲面論との比較と,極大曲面に現れる特異点,および de Sitter 空間の平均曲率1の曲面について解説します. |
| |
|
|
| 15:00-16:00 |
|
さまざまな曲面の完備性へのOsserman の補題の応用(梅原) |
| |
|
特異点をもつ曲面の完備性と弱完備性との間の関係を調べるのにOsserman の補題が重要な役割を果たすことを示します. |
| |
|
|
| 16:30-17:30 |
|
弱完備性と有界な極大曲面(山田) |
| |
|
グラナダ大のMartin氏と3人の共同研究の内容を解説します. |
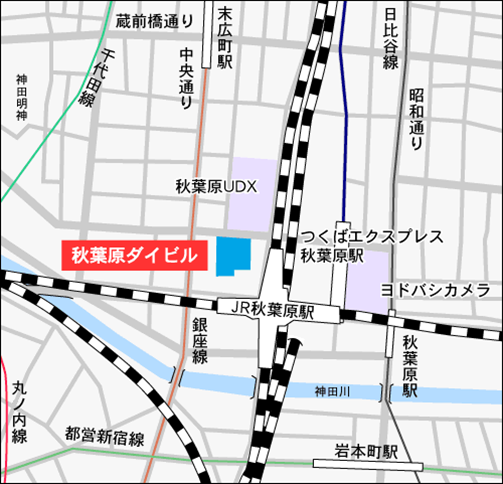
アクセス:
| JR 山手線・京浜東北線・総武中央線 |
「秋葉原駅」 |
徒歩約1分 |
| つくばエクスプレス |
「秋葉原駅」 |
徒歩約2分 |
| 東京メトロ日比谷線 |
「秋葉原駅」 |
徒歩約5分 |
| 東京メトロ日銀座線 |
「末広町駅」 |
徒歩約5分 |
ポスター:

リンク
問合せ先: 酒井 高司 sakai-t (at) tmu.ac.jp
秋葉原微分幾何セミナーのページへ戻る


