Let
![]() be a sequence of signals. Then
forward autoregressive (AR) model of order m is given by
be a sequence of signals. Then
forward autoregressive (AR) model of order m is given by
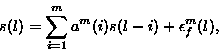 |
(1) |
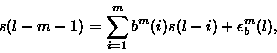 |
(2) |
PARtial autoCORelation (PARCOR) coefficients are often used in speech
signal processing and are often more useful than AR
coefficients
![]() or
or
![]() .
PARCOR
coefficient Pm of order m is defined as a correlation coefficient
between forward and backward prediction errors in the autoregressive
model of order m - 1. Namely,
.
PARCOR
coefficient Pm of order m is defined as a correlation coefficient
between forward and backward prediction errors in the autoregressive
model of order m - 1. Namely,
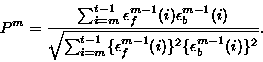 |
(3) |
There is a fast recursive algorithm for calculating AR and PARCOR coefficients. The algorithm can compute all AR and PARCOR coefficients of orders 1 through m with O(m2) [11].
For online computation of PARCOR coefficients, we can use the
recursive formula with forgetting factor
![]() to
estimate the autocorrelations r(l) as
to
estimate the autocorrelations r(l) as
| (4) |