

Next: Experiments
Up: Gesture Recognition using HLAC
Previous: Higher Order Local Autocorrelation
To cope with nonuniform changes in the speed of gesture,
HLAC feature vectors extracted from the sequences of PARCOR images are
fed into a recognizer based on Hidden Markov Models.
Let each gesture be represented by a sequence of HLAC feature vectors
defined as
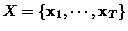 .
Each vector
.
Each vector 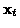 contains HLAC features extracted from PARCOR images at time t. Then
the gesture recognition problem can be formulated as that of finding
the class Ck which has the maximum posterior probability
P(Ck|X). By using Bayes' rule, the posterior probability can
be written as
contains HLAC features extracted from PARCOR images at time t. Then
the gesture recognition problem can be formulated as that of finding
the class Ck which has the maximum posterior probability
P(Ck|X). By using Bayes' rule, the posterior probability can
be written as
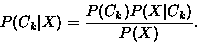 |
(6) |
Thus, for a given prior probabilities P(Ck), the most
probable gesture can be found by estimating the likelihood P(X|Ck).
In HMM based recognition, it is estimated by assuming a parametric
model of gesture production as a Markov model with hidden states
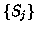 .
In the following experiments, we tried a simple left to
right HMM with 7 states shown in Figure 3 for all
gestures. To improve the recognition rate, we have to determine
suitable model for each gesture. We also assumed the HLAC feature
vectors are generated from Gaussian densities
.
In the following experiments, we tried a simple left to
right HMM with 7 states shown in Figure 3 for all
gestures. To improve the recognition rate, we have to determine
suitable model for each gesture. We also assumed the HLAC feature
vectors are generated from Gaussian densities
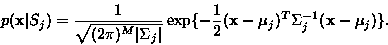 |
(7) |
Figure 3:
State transition model.
 |
To learn the parameters of the HMM from the training examples, we used
the well-known Baum-Welch algorithm.


Next: Experiments
Up: Gesture Recognition using HLAC
Previous: Higher Order Local Autocorrelation
Takio Kurita
1998-03-13
![]() .
Each vector
.
Each vector ![]() contains HLAC features extracted from PARCOR images at time t. Then
the gesture recognition problem can be formulated as that of finding
the class Ck which has the maximum posterior probability
P(Ck|X). By using Bayes' rule, the posterior probability can
be written as
contains HLAC features extracted from PARCOR images at time t. Then
the gesture recognition problem can be formulated as that of finding
the class Ck which has the maximum posterior probability
P(Ck|X). By using Bayes' rule, the posterior probability can
be written as