Research Topics
Graphene see
Non-equilibrium Superconductivity see
Single Charge Tunneling see
Commensurability Mangetoresistance Oscillations (AMRO and Weiss oscillation) see
a) new Low energy band structure of graphene & new Intrinsic resistance peaks (ridges)
b) Ballistic transpor in graphene antidot lattices
c) Phase coherent transport in graphene antidot lattices
d) Making encapsulated graphene
e) Making suspended graphene
f) Making graphene from graphite intercalation compounds
g) CVD growth of the topological insulators
a) Low energy band structure of graphene
NEW: Low energy band structure of
graphene. How the atomic layers aquire a bulk character. Yagi et al.
Sci. Rep.
8, 13018 (2018).
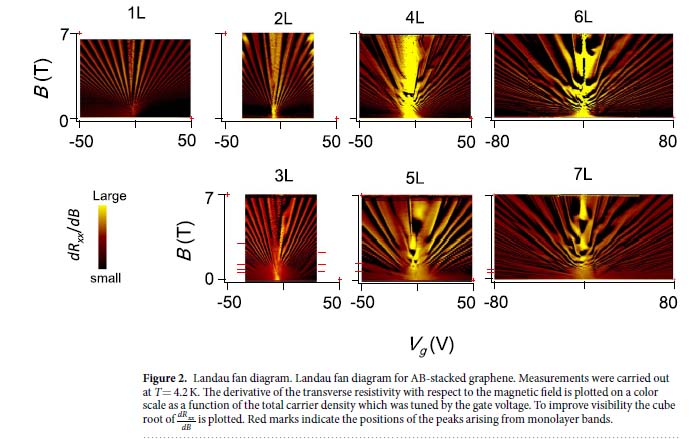
We have measured the Landau fan diagram of one to 7 layer graphene (AB-stacking). Even odd layer number effect was clearly observed.
Keywords: Landau fan diagram, monolayer, bilayer, trilayer, tetralayer, pentalayer, hexlayer, heptalayer, graphene

NEW: Multilayer graphene shows intrinsic resistance peaks in the carrier density dependence.
Sci. Rep. 8 13992
(2018). DOI: 10.1038/s41598-018-32214-7.
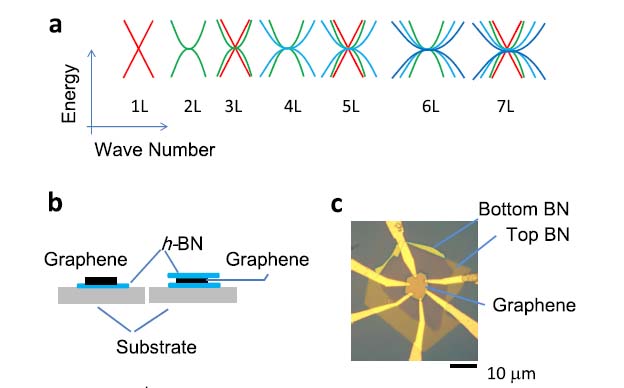
Tetralayer graphene shows intrinsic resistance peaks in the gate voltage dependence of resistance at zeromagnetic fields. These peaks originate from band structure.
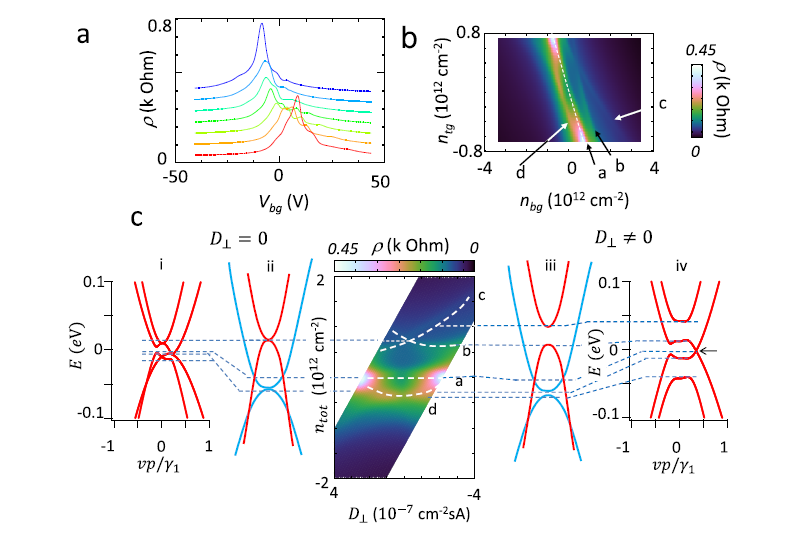
Tetralayer graphene (a)Backgate voltage dependence of resistance shows complicated peaks, which varies with top gate voltages. (b) A map of resistivity as a function of carriers induced by top and bottom gate voltages. (c) A map of resistivity as a function of carrier density and perpendicular electric flux density. Resistance ridges are discernible.
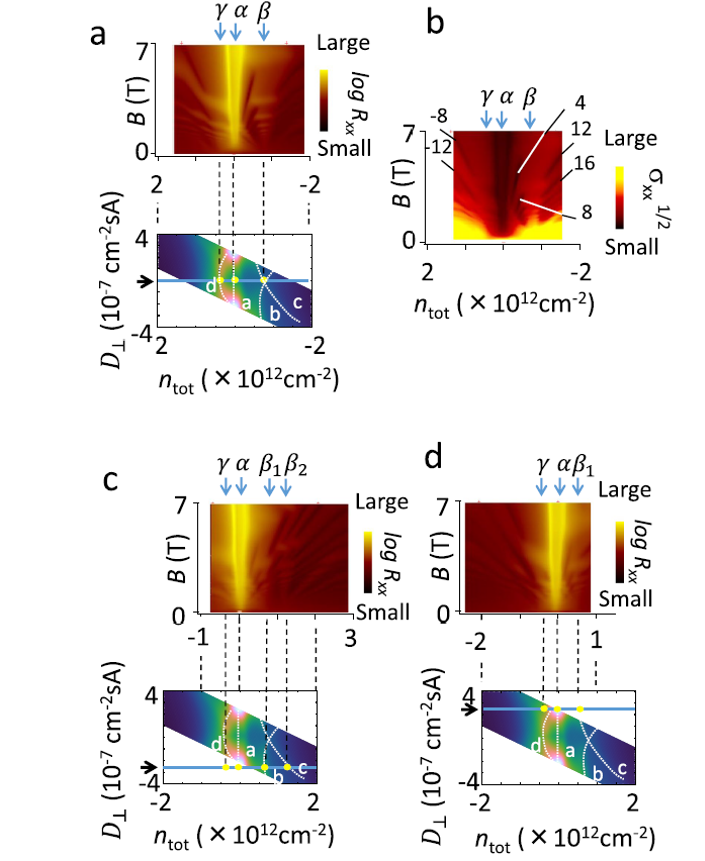
Landau fan diagrams of tetralayer graphene and the ridge structure. The resistance ridge corresponds to the zero-mode Landau levels which split in non-vanishing perpendicular electric flux density.
Similar but different resistance ridges were observed in hexlayer graphene.
Ballistic Transport in Graphene Antidot Lattices
R. Yagi et al.Phys. Rev. B 92,
195406 (2015).
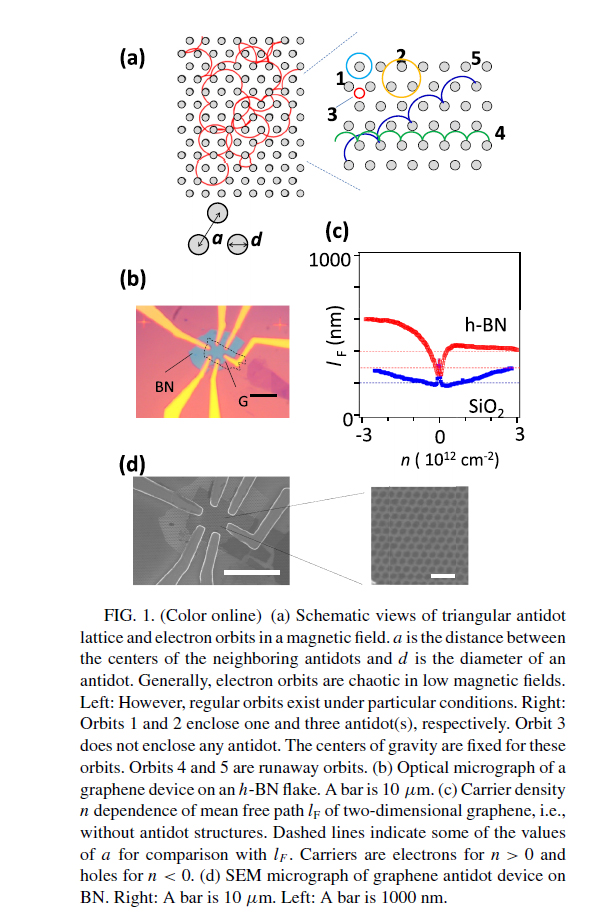
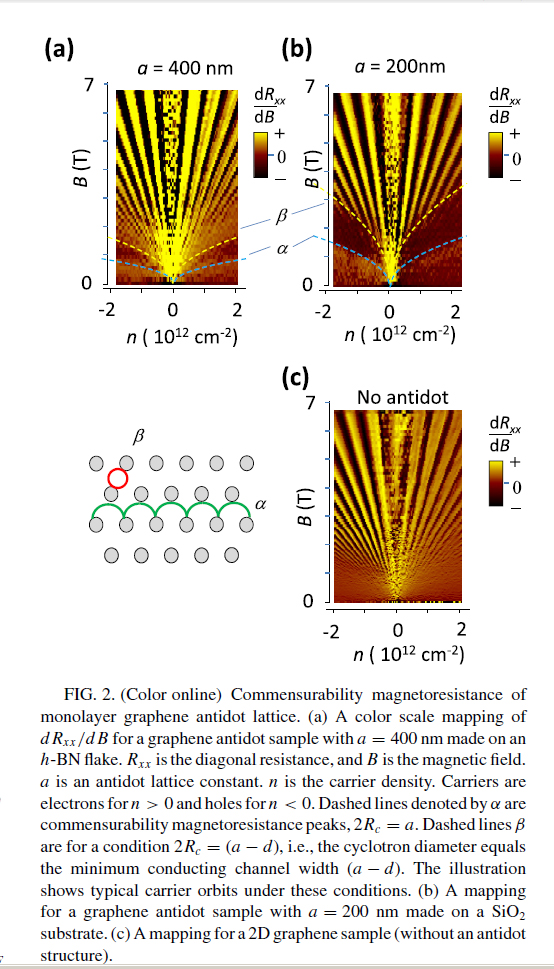
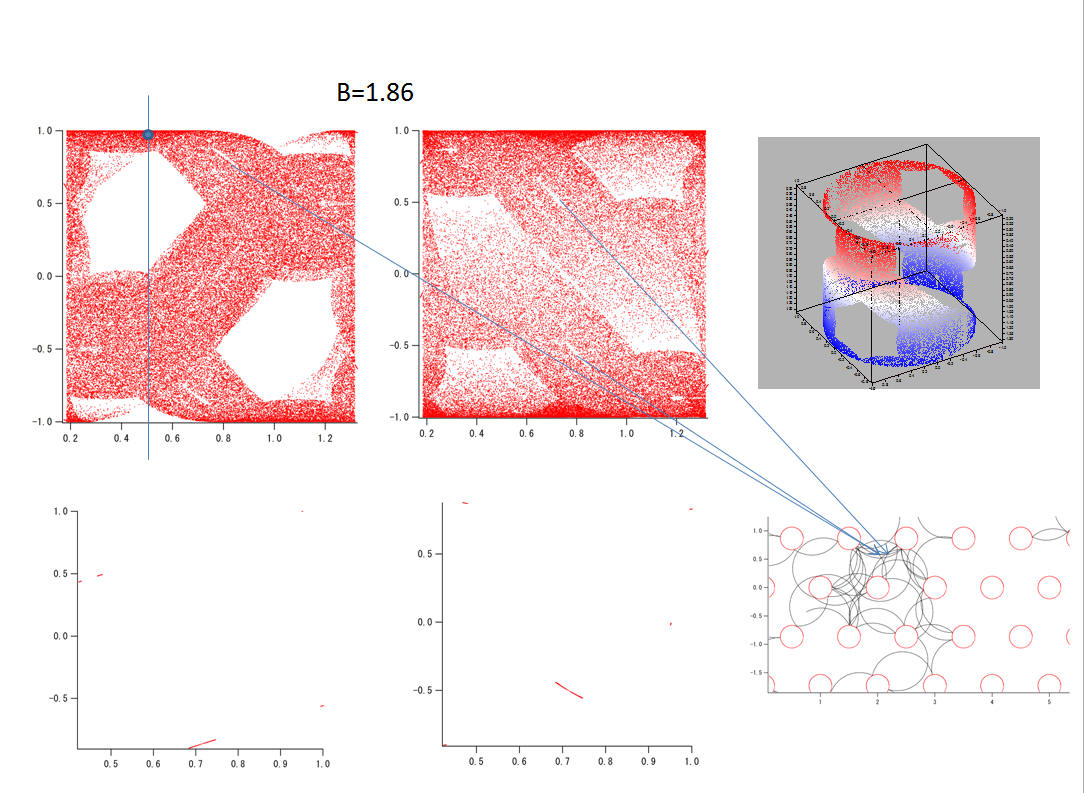
Poincare Section
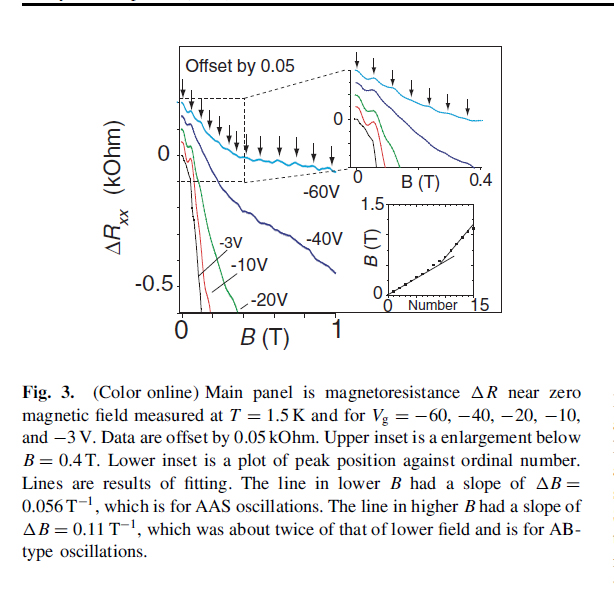
Observation of Altshuler Aronov Spivak (AAS) Oscillation in Graphene
Yagi et al.
J. Phys. Soc
Jpn. 81, 063707 (2012).
The AAS oscillation arises from quantum interference of a pair of electrons with time reversal symmetry, which are backscatterd coherently. This is the first observation in graphene system.
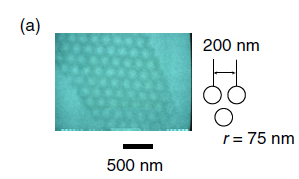
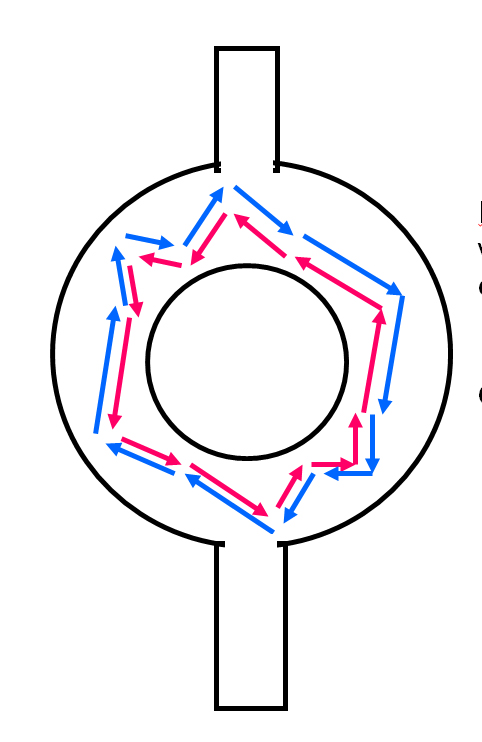
SEM of Antidot Lattice Sample. Trajectories of coherently back scattered electrons, which are symmetric in time reversal.
Suspended Graphene
Graphene placed directly on the SiO2 substrate is influenced by charged impurity in the substrate. This results in a limited electronic mobility. Much higher mobility can be attained by suspending graphene. The image below is a photo of suspended monolayer graphene that was made by us.

Studies on methods of making graphene
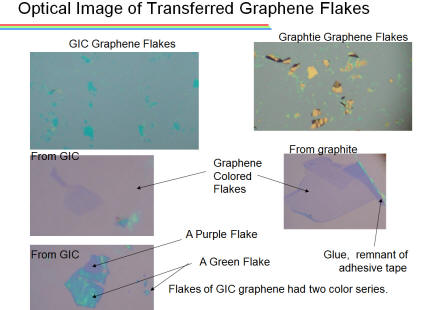
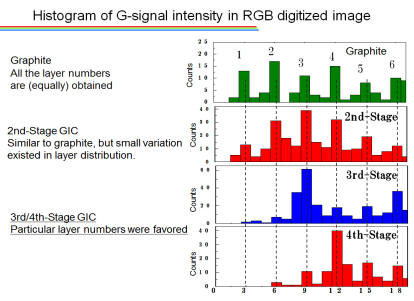
Making Graphene From Graphite Intercalation Compounds
S. Fukada et al.
Jpn. J. Appl. Phys.
51,
085101 (2012).
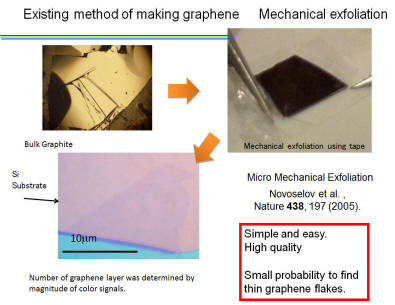
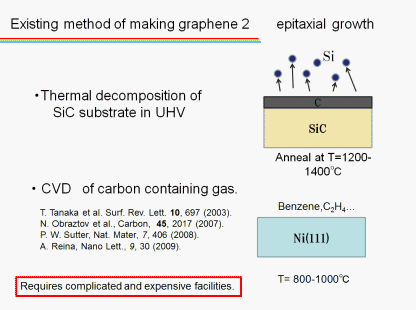
We can make graphene easily in principle by making graphite thinner and thinner with adhesive tape. It does not require any special facilities. However it is hard making graphene with a few layer number or less. Sometimes we may not obtain sufficiently thin graphene, and sometimes we may not obtain graphene with sufficiently large sizes by the simple method. How can we overcome it.



CVD growth of Topological Insulators
Bi2Se3 Single Crystal
2. Non-equilibrium Superconductivity
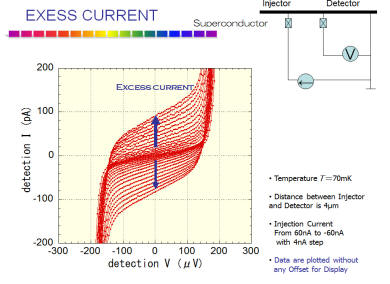
a) Observation of charge imbalance and excess current
b) Relaxation of charge imbalance due to pair breaking pertubations
a) Observation of charge imbalance
R. Yagi
Phys. Rev. B
73,
134507- (2006).
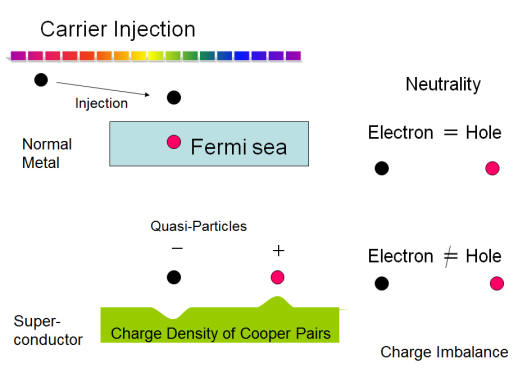
What is Charge Imbalance of Non Equilibrium Superconductivity?
Quasi-particles in superconductors are excitations from the ground state of superconducting condensate. They are single particle state. If you inject electrons into a superconductor, the injected electrons become quasi-particles for a while before they are converted to Cooper pairs or superconducting condensate. Although quasiparticles are single particle state, they are not single particle electron itself, but are quantum-mechanical superposition of electron and holes. They have fractional charges that depend on ratio of the weight for superposition, which is determined by energy of injection.

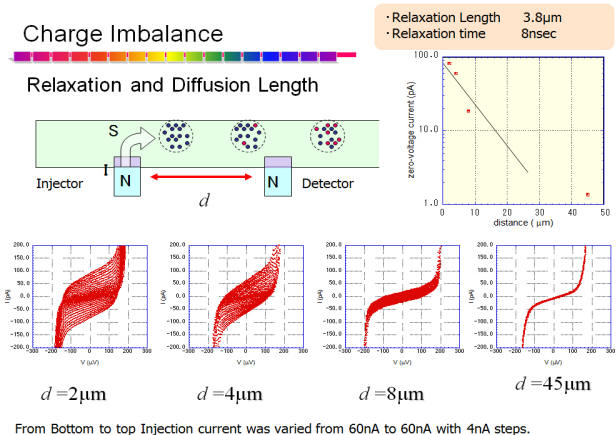
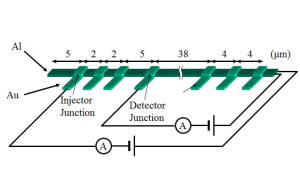
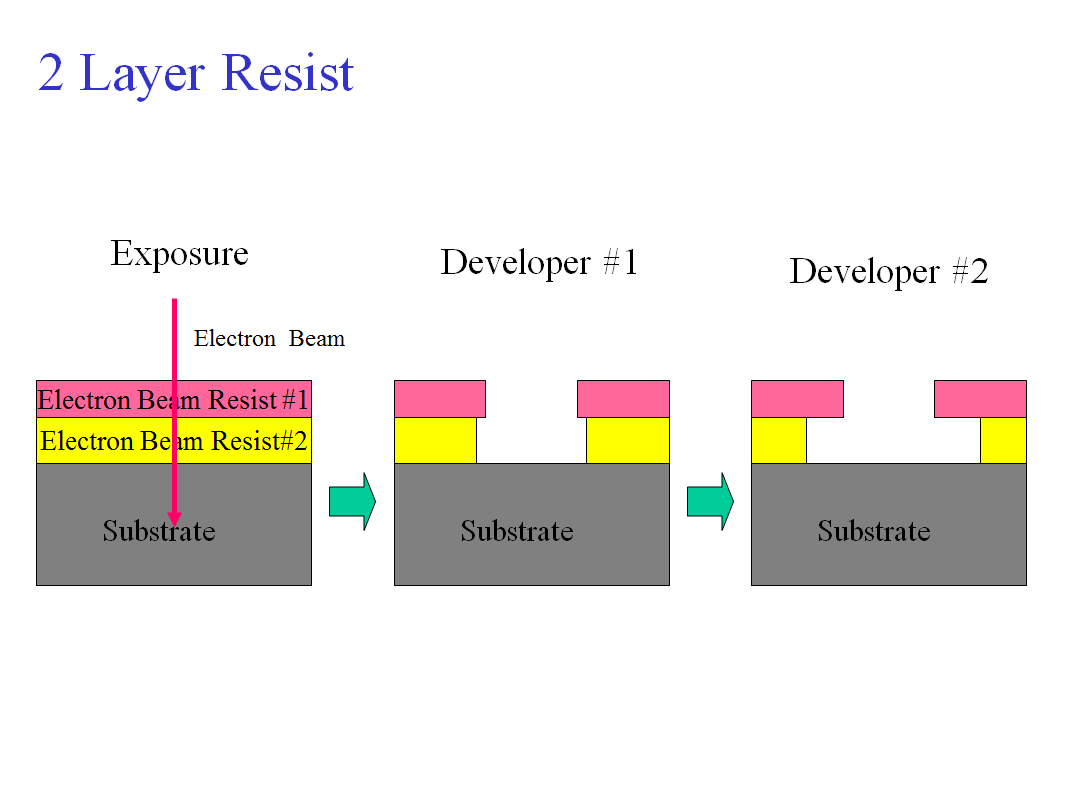
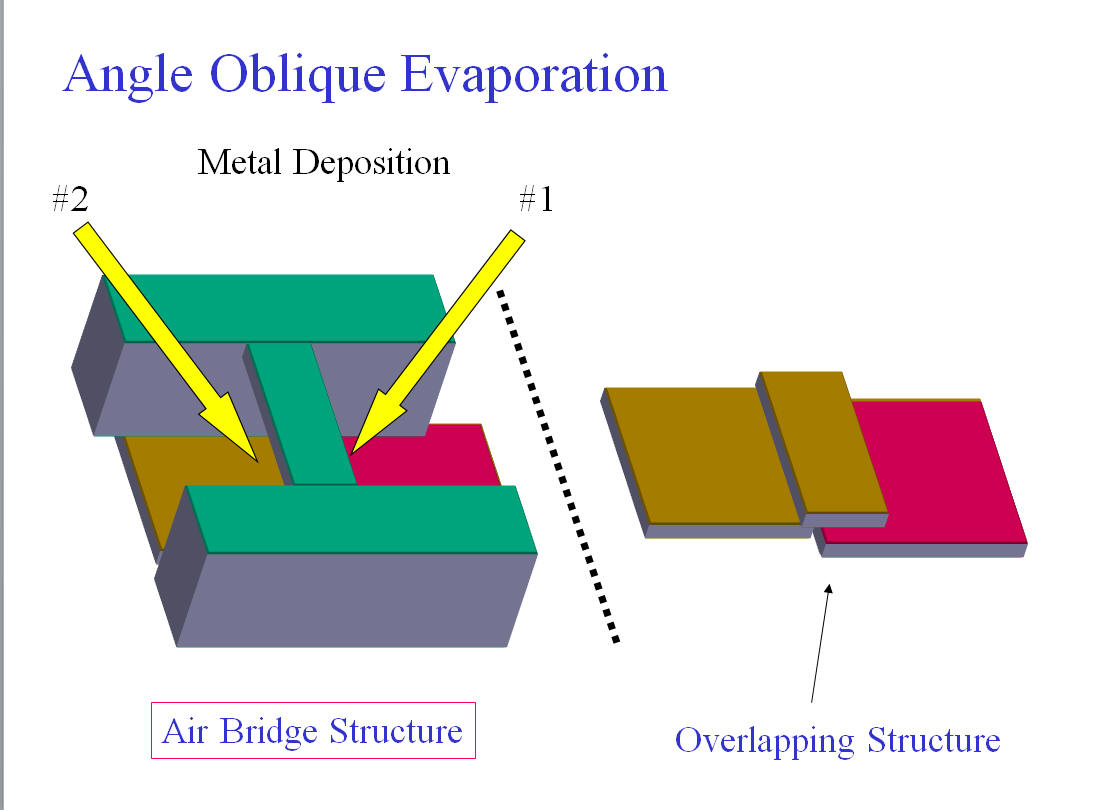
Then, how to make ultra-small tunnel junctions? It is easy. We used double layer resist and angle oblique evaporation technique. We made bridge structure that can be formed by the overhang structure of PMMA and the co-polymer resist. Then tunnel junction was formed by depositing metals different angles and oxidation between each evaporation process.
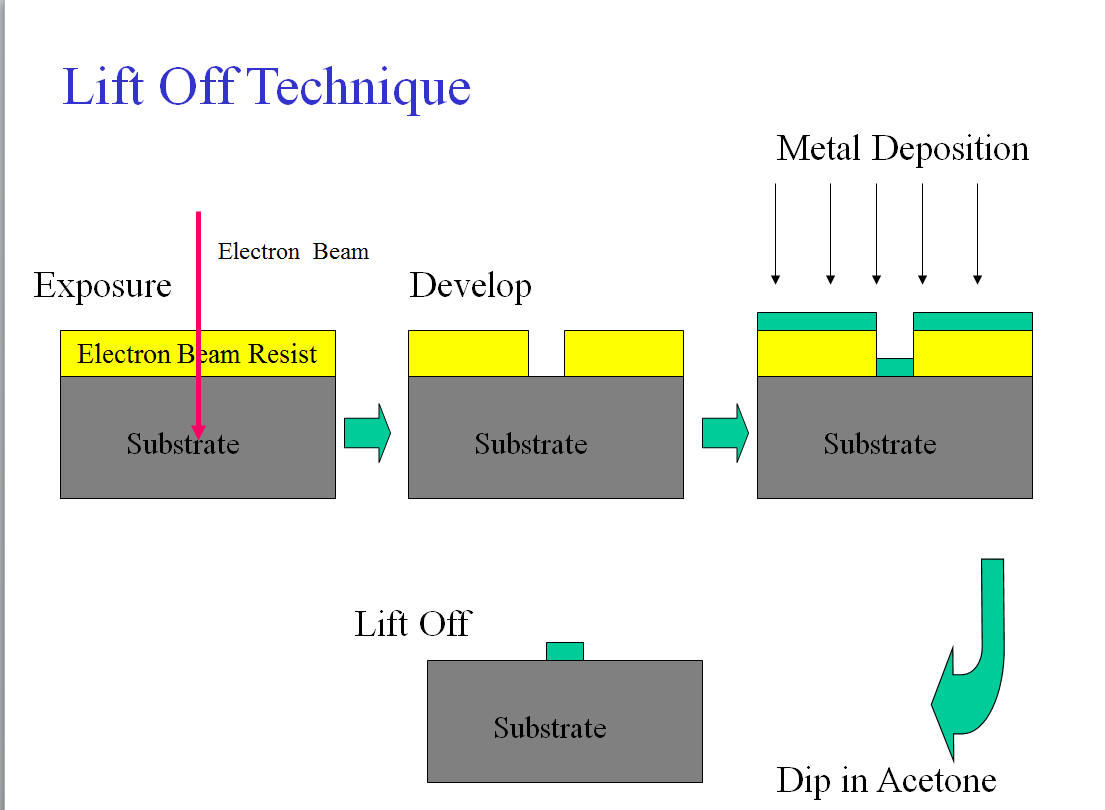
**
a) Dissipative Phase Transition in Resistively Shunted Small Josephson Junctions
b) Superconductor-insulator transition in two-dimensional array of small Josephson junctions
c) All Chromium Single Electron Transistor
a) Dissipative Phase Transition and Macroscopic Quantum Coherence in Resistively Shunted Small Josephson Junctions
R. Yagi and S. Kobayashi, J. Phys. Soc. Jpn. 66 3722-3724 (1997). Takahide Yamaguchi et al. Phys. Rev. Lett. 85 1974-1977 (2000).
Superconductor-insulator transition in a single ultra-small tunnel junction was successfully tuned by external shunt resistor. This is a proof of dissipative phase transition for macroscopic quantum coherence. The phase variable of superconducting condensate obeys differential equation that is equivalent to the Newton's classical equation of motion. If capacitance of a tunnel junction is sufficiently small, the uncertainty principle between the phase variable and an electron number relevant to a charging effect, results in quantum mechanical behavior. The system is under influence of quantum tunneling and coherent quantum states. External shunt resistor gives dissipation in this quantum system. As pointed out by Caldeira and Legett, dissipation reduces quantum tunneling rate. This leads to a phase transition between quantum regime and classical regime at a critical value of dissipation, which is given by quantum resistance h/4e2 for a single Josephson junction.
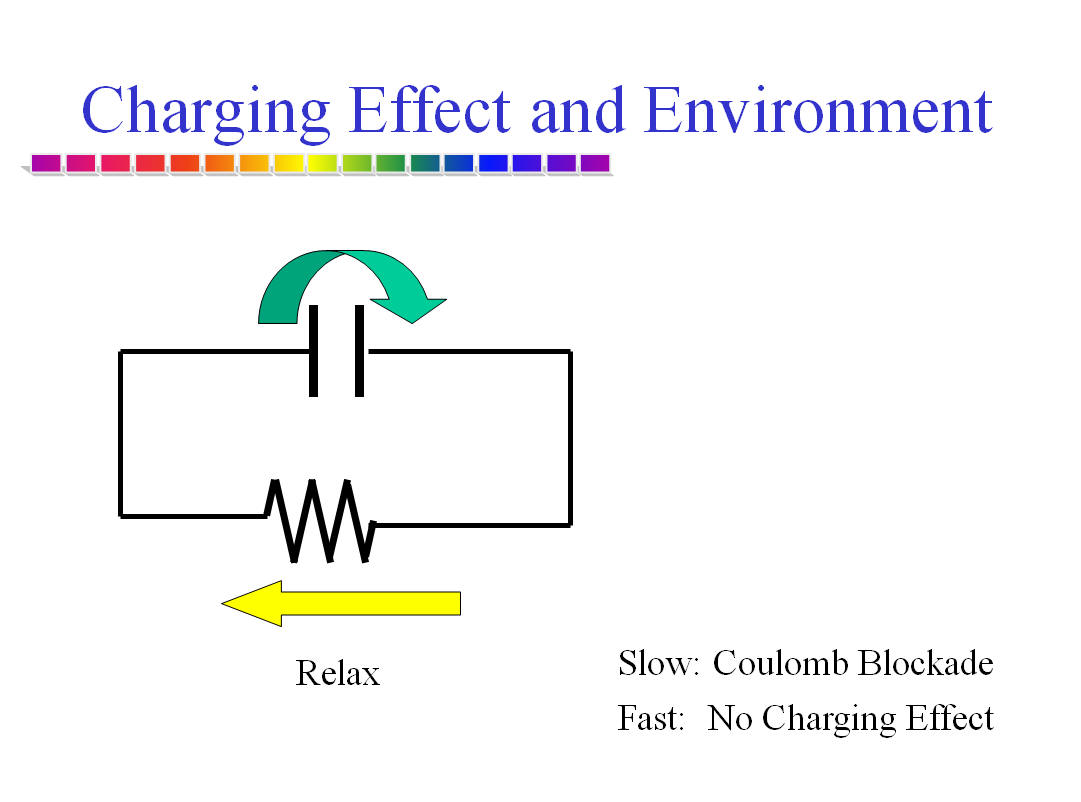

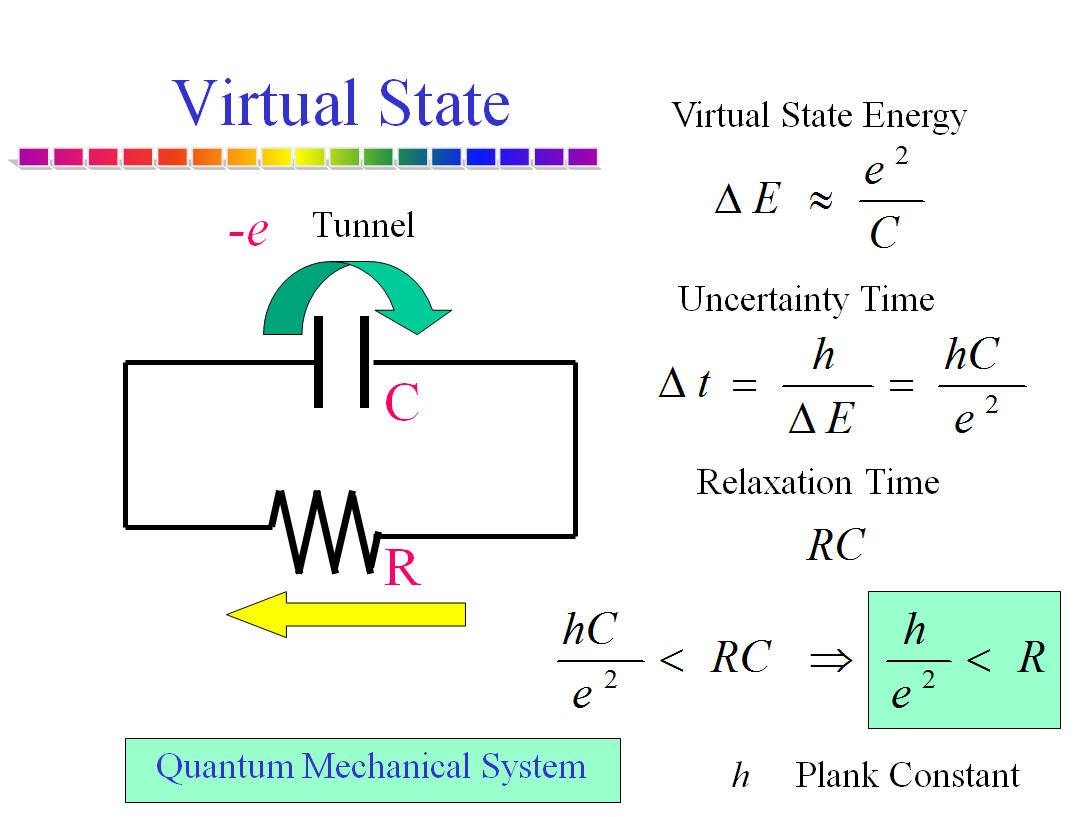
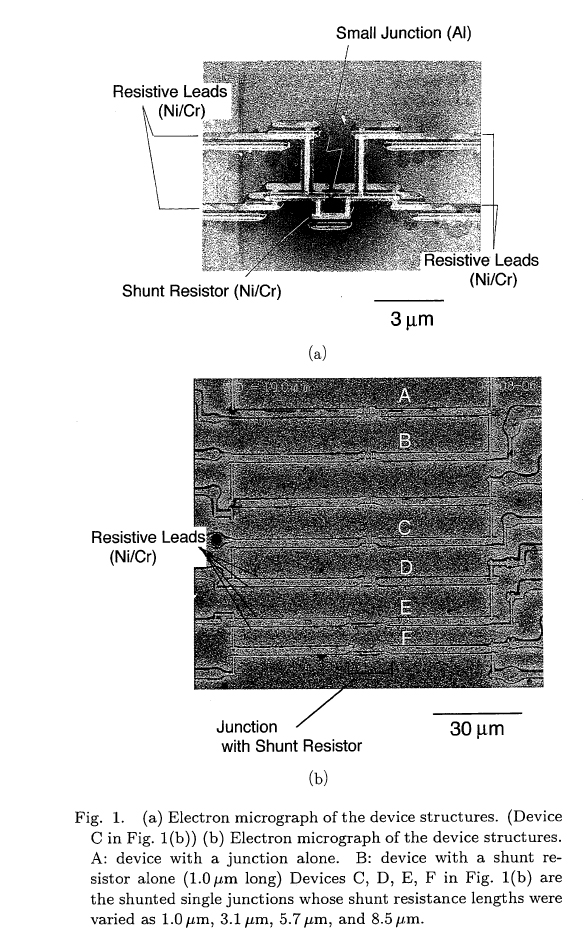
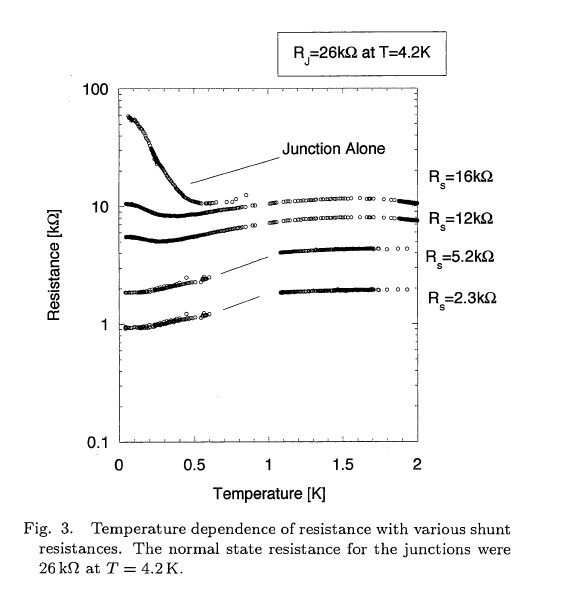
b) Superconductor-insulator transition in two-dimensional array of small Josephson junctions
Under Construction.
c) All Chromium Single Electron Transistor
Kubota and Yagi,
Physica B, 383, 57-58 (2006).
For practical purposes, single electron devices should be operated in normal state to avoid difficulties and complication due to phase transition, such as superconducting state. However ultra-small tunnel junctions with normal state metal are hard to realize because a limited number of metals are available for making high-quality tunnel barrier by oxidating the metal surface. We have realized all chromium single electron transistor that consists of metal junctions in normal state even at zero magnetic fields. Tunnel barrier was formed by plasma oxidation.

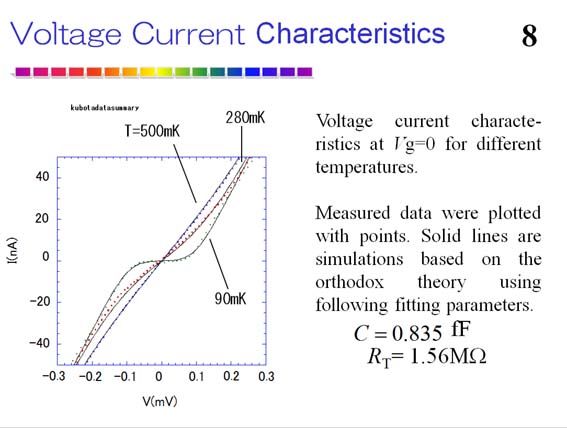
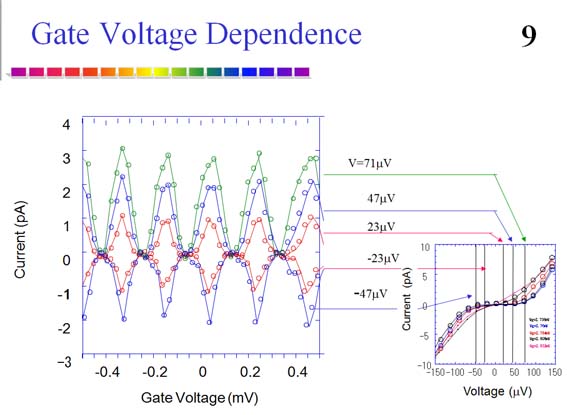
Principle of Operation

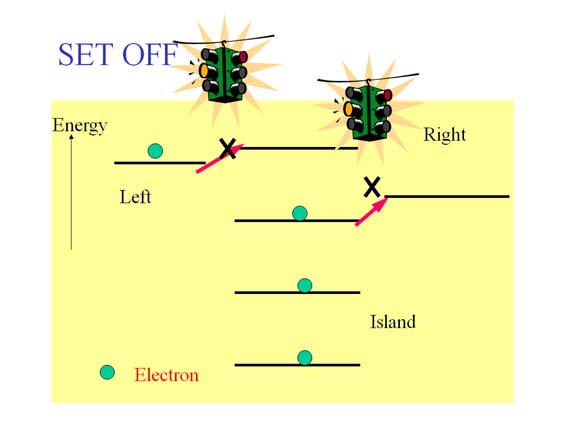
4 Commensurability Magnetoresistance Oscillation
a) Semiclassical interpretation of the angular dependent magnetoresistance oscillations (AMRO) in quasi two dimensional systems
b) Observation of angular dependent magnetoresistanceoscillations (AMRO) in semiconductor superlattices
c) AMRO for various fermi surfaces
d) Magnetic Weiss oscillations
a) Semiclassical Transport Theory of AMRO. R. Yagi et al. J. Phys. Soc. Jpn. 59 (1990) 3069-3072; R. Yagi, Thesis, the Univ. of Tokyo (1992).
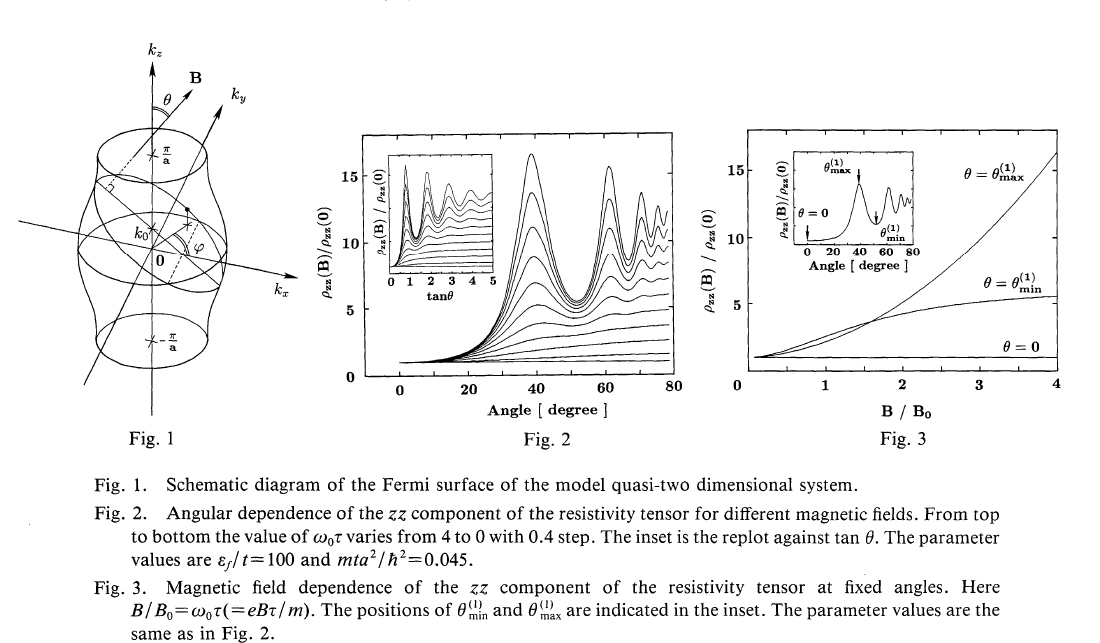
b) AMROs for various fermi surface shapes.
R. Yagi and Y. Iye,
Solid State Commun.
89(1994)275-281.
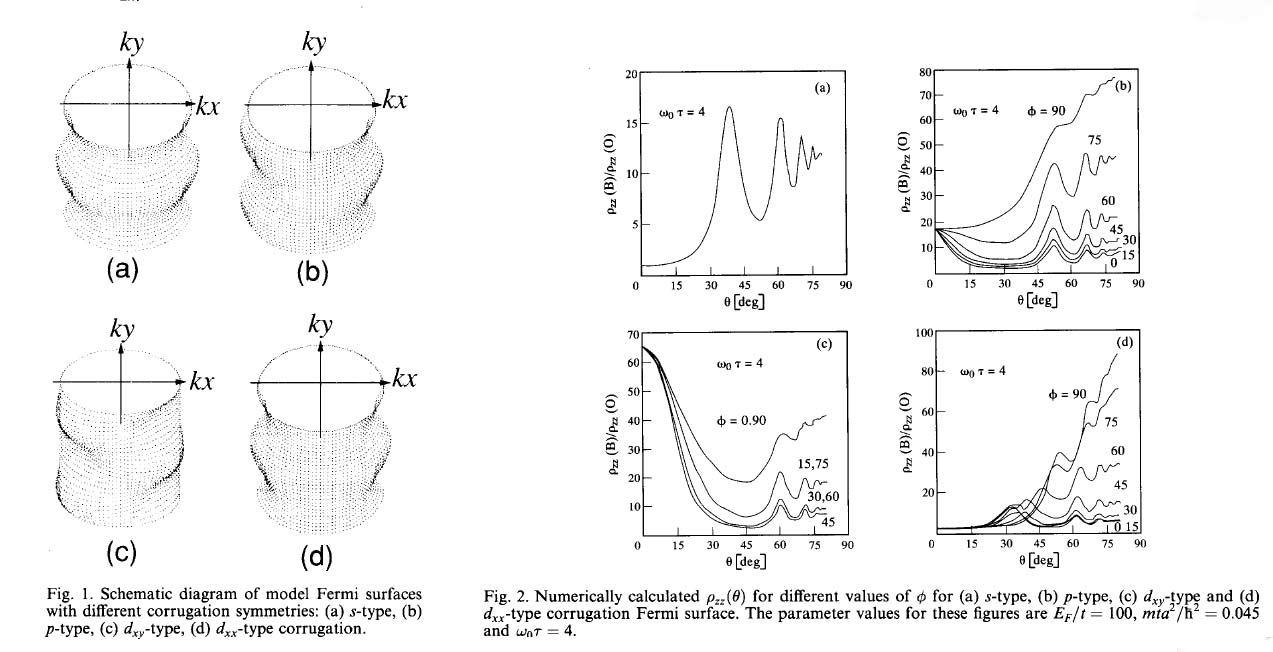
c) AMRO in Semiconductor Superlattices
R. Yagi et al.
J. Phys. Soc. Jpn.
60(1991) 3784-3791.
The first observation of AMRO in systems other than organic conductors.
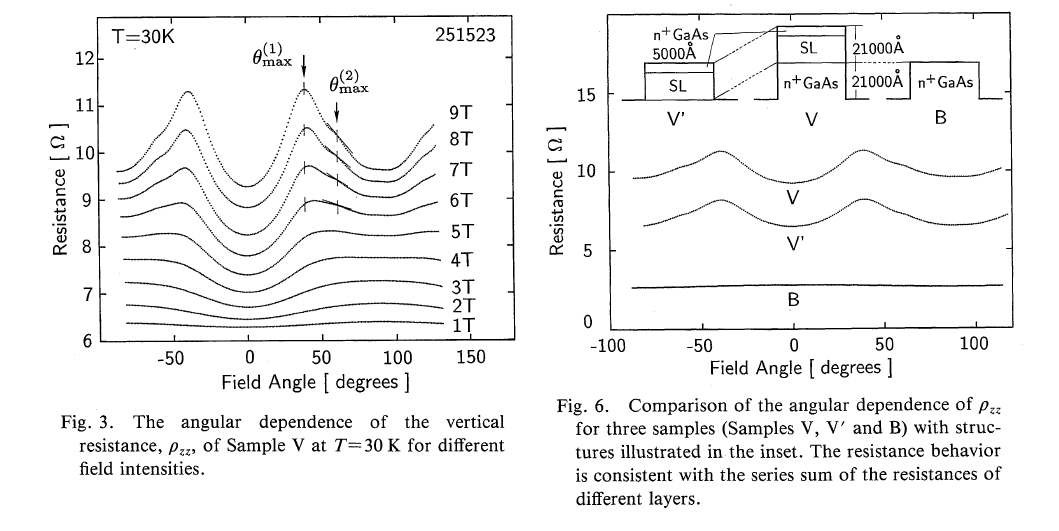
d) Magnetic Weiss Oscillation R. Yagi et al. J. Phys. Soc. Jpn., 62 1279-1285 (1993); R. Yagi, Thesis, the Univ. of Tokyo (1992).
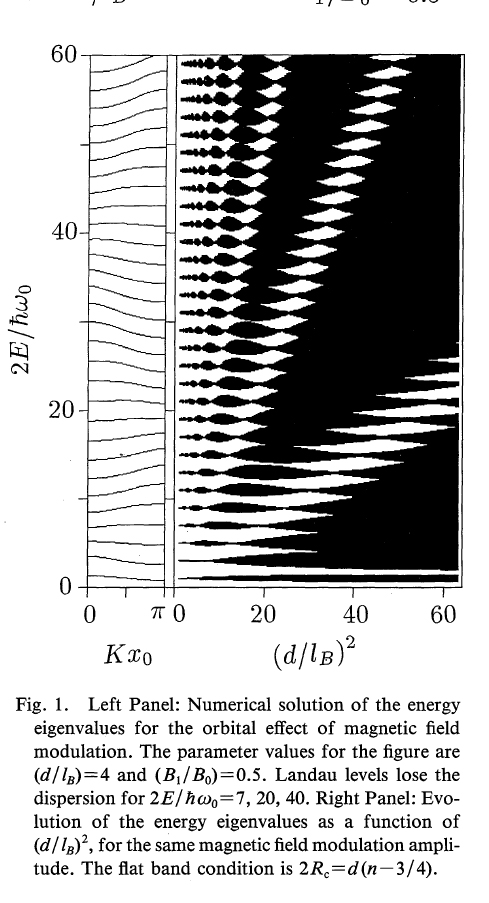
Quasi-Two-dimensoional Electron System