コンテンツ
定積分の近似値
これまでfor文を使うことで、![]() や
や![]() を表現することができることを実感してもらったと思います。
を表現することができることを実感してもらったと思います。
そこで、積分が和の極限だということを使うと,計算機で定積分の近似値を簡単に計算できます。
以下は定積分
![]()
の近似値を(区分求積法を使って)求めるプログラムです。
integration-1.cとして打ち込み実行してください。
プログラムの概要は以下の通り。
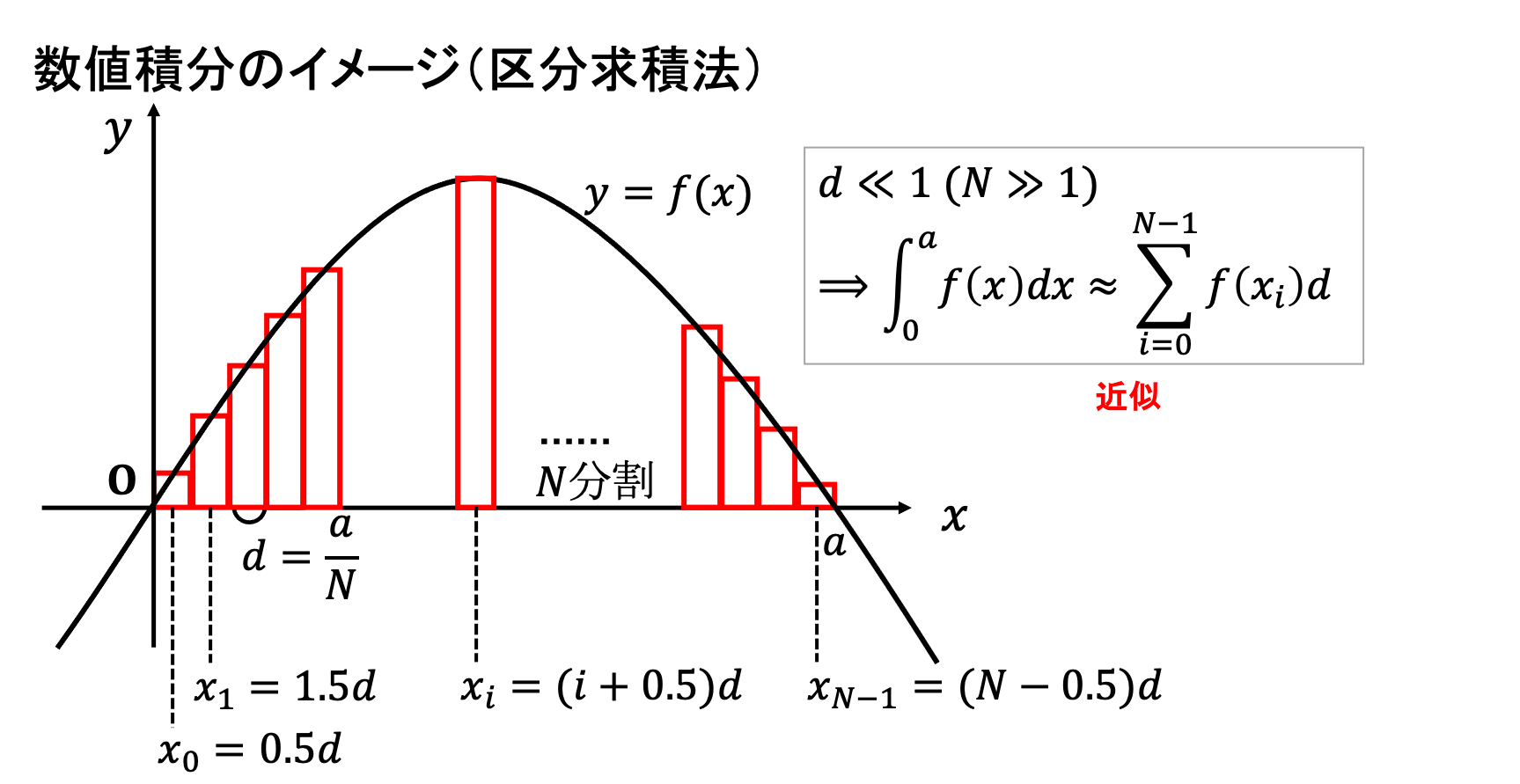
- まず積分区間(0~ a)を、 N 個(i = 0,…, N-1)の、幅 d = a/N の領域に分割。
- i 番目の領域の中心(x = (i+0.5)*d)での関数の値(y = f(x)=1 – x*x)を高さとする長方形の面積が y*d と得られるので、それらを全区間に渡って足し合わせる。(紙に絵を描いてみるとすぐ分かります。)
integral-1.c
#include <stdio.h>
int main() {
/* 実数型変数の宣言 */
double f, x, y, a, d;
/* 整数型変数の宣言 */
int i, N;
/* 積分範囲 を代入 */
a = 1.0;
/* 分割数 N を代入 */
N = 100;
/* 分割の幅 d を計算. 整数型変数 N を,ここでだけ実数型として扱って計算(下の注を参考)*/
d = a / (double)(N);
/* fの初期化 */
f = 0.0;
/* 積分を計算する繰り返し文 */
for (i = 0; i < N; i++) {
x = (i+0.5) * d;
y = 1.0 - x * x;
f = f + y * d;
}
/* 結果を表示 */
printf(" 答え %lf \n", f);
return 0;
}
– – – – – – – – – – – – – – – –
分割数 N を大きくすると(例えば 10 -> 100 -> 1000 としていくと),2/3=0.66666・・・に近づくことを確認してください。
注:プログラムの途中で、一時的に変数の型を変更すると便利な事があります。(上の例での N, i 等)このような場合「(一時的に使用したい変数の型)(変数)」とすることで、一時的にその部分でのみ指定した型の変数として扱う事ができます。つまり, 例えばプログラム始めで double a; と宣言されていても、ある文中で (int)(a) 書かれていれば、その部分のみでは a は int 型変数として扱われます(その部分以外のところでは、始めに宣言された型で扱われます)。(int)(a), (double)(N) 等, 整数型, 実数型どちらでも使用可です(例えば a = 2.9 等の場合 (int)(a) は 2 となります。実数型変数を整数型にした場合、小数点以下は 0 になります)。
課題1
例えば積分区間を -2 ~ 3 とした場合の定積分の近似値を計算求めよ。
また適当な関数、積分区間でいろいろ計算してみてみよ。
数学関数
数学関数の使い方
C言語では下記プログラムのように、様々な数学関数を用いることができます。
例えば以下のようなプログラムで、三角関数の計算や平方根等の利用ができます。
(math-1.c として打ち込んでみてください。)
math-1.c
#include <stdio.h>
#include <math.h>
int main() {
double pi,a,x,y,z,r;
pi = 3.14159265;
a = 3.0;
r = 10.0;
/*三角関数の計算 */
x = r*cos(pi/a);
y = r*sin(pi/a);
/*平方根の計算 */
z = sqrt(x*x + y*y);
printf("10*cos(pi/3.0)=%lf, 10*sin(pi/3.0)=%lf \n", x, y);
printf("A square root of (x*x+y*y) is %lf \n", z);
return 0;
}
数学関数を用いる場合には、
#include <math.h> をプログラムの先頭付近に書き入れることと、コンパイル時に、
ファイル名を math-1.c とすると、
gcc math-1.c -o math-1 -lm
というふうに、最後に -lm を付け足す必要があります。
sin(), cos(), sqrt()の他に, exp(), tan(), log() などいろいろ用意されています。
さらに、円周率![]() も変数”M_PI”として宣言されていますので、今後はこちらを使っても良いです。
も変数”M_PI”として宣言されていますので、今後はこちらを使っても良いです。
(次回以降、よく使う事になります.)
課題2
実数x の値の入力を促し、sin(x)、cos(x)、tan(x)の値を出力するプログラムを作成せよ。
課題3
実数x , hの値の入力を促し、(sin(x + h) – sin(x) )/ h、cos(x)の値を出力するプログラムを作成せよ。
また、同じxの値を与えた場合で、h = 0.1, 0.01, 0.001とおいたときの出力を確認せよ。
課題4
二等辺三角形ABCの角Aの大きさをx (rad)、辺ABと辺ACの長さを共にLとする。
xとLの値の入力を促し、辺BCの長さを求めるプログラムを作成せよ。
課題5
整数Nの入力を促し、半径10の円に内接する正N角形の周りの長さ、面積を求めるプログラムを作成せよ。
(正四角形、正六角形の場合について正しい答えになっているか、またNが大きい場合に円に近い値をとるか、各自試してみよ)
課題6
実数L>0の入力を促し、![]() をxについて区間[0, L]で積分するプログラムを作成せよ。
をxについて区間[0, L]で積分するプログラムを作成せよ。
実数型変数の絶対値は数学関数fabs()をもちいて計算できる。(例:実数型変数xの絶対値はfabs(x) )
ただし、区間の分割数nは1000であるとする。
方程式の解の求め方(最も簡単な例)
区分求積法と同じように区間を区切って考えることで、定義域が定められた方程式の解を近似的(数値的に)に求めることもできます。例えば、方程式の例として
![]()
を考えてみましょう。数値的に求める必要もなく、定義域での解は![]() の1つのみであることは明白でしょう。これをあえて数値的に解いてみます。下の図のような線形近似が最も簡単な方法です。
の1つのみであることは明白でしょう。これをあえて数値的に解いてみます。下の図のような線形近似が最も簡単な方法です。
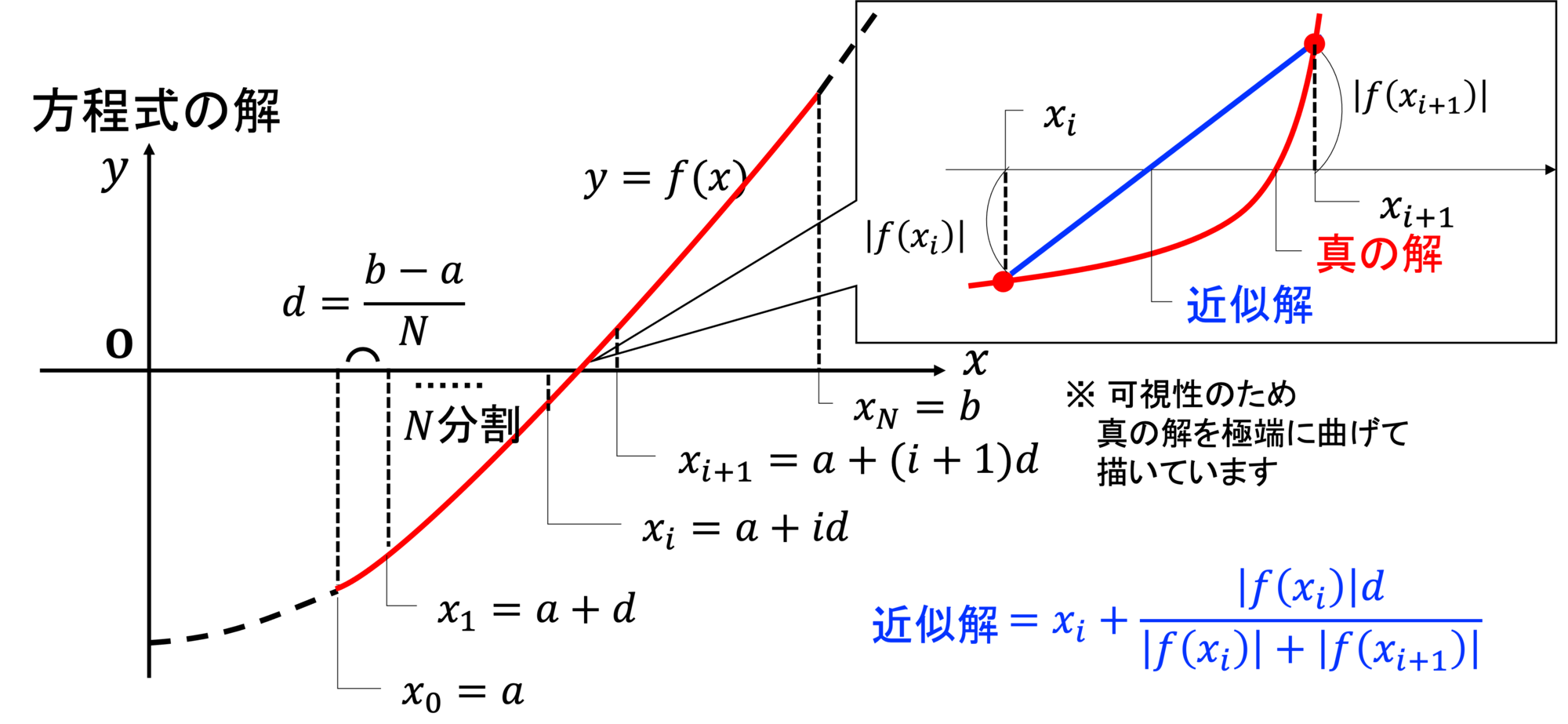
x方向にN分割し、x軸を跨ぐ区間を見つけ、直線で近似(線形補完という)し、近似解を求めます。下にサンプルプログラムを置いておきますので、参考にしてください。
solve.c
#include <stdio.h>
#include <math.h>
int main() {
int i, N = 10000;
double x_l, x_r, fx_l, fx_r;
double a = 1., b = 3.; // 定義域の下限と上限
double d = (double)(b - a)/N; // 刻み幅
// 定義域の下限が交点の場合
if (a * a - 4.1 == 0.0) {
printf("%lfは近似解の1つです。\n", a);
}
// 区間(x_i,x_{i+1}]の範囲に交点がないかを探していく
for (i = 0; i < N; i++) {
x_l = i * d + a; // x_i
x_r = (i+1) * d + a; // x_{i+1}
fx_l = x_l * x_l - 4.1; // f(x_i)
fx_r = x_r * x_r - 4.1; // f(x_{i+1})
if (fx_r * fx_l <= 0. && fx_l != 0.) {
// 区間(x_i,x_{i+1}]交点を含む場合は、関数の符号が逆転する
printf("%lfは近似解の1つです。\n", x_l + d * fabs(fx_l)/(fabs(fx_r) + fabs(fx_l)));
}
}
return 0;
}
※ 数値誤差が発生する可能性があります。solve.cの場合、本来であればx_lやx_rにNをかけたら整数値(=iやi+1)になるはずです。しかし、実はsolve.cにおけるd=2./10000はコンピュータにとっては切りのいい数字ではありません。そのため、切り捨て誤差と呼ばれる誤差が発生し、x_lやx_rにNをかけても整数値にならないことがあります。
課題7
刻み数Nを変えたときに近似解がどう変わるか確認せよ。
線形補完は最も簡単な方法ですが、高い精度を実現しようとするとNを非常に大きくしないといけません。そのため、二分法や勾配法といったより精度の高い方法がありますので、興味があったら調べてみてください。
小ネタ
どれだけ精度を上げようとも、printf関数で出力した結果は小数第六位までです。表示桁数を変えるには、printf関数内の%lfを変える必要があります。以下はmath.hで定義されているM_PI (![]() のこと)を使った表示例です。
のこと)を使った表示例です。
%lf :3.141593 %11lf : 3.141593 %11.lf : 3 %.11lf :3.14159265359 %03.lf :003 %5.2lf : 3.14 %05.2lf:03.14
“%X.Ylf”とすることで、「小数点第Y位まで、かつ、(小数点含めて)全部でX文字で表示する」ことができます。さらにXの前に0をつけると、左側の空いている部分を0で埋めるようになります。”.Y”がない場合は、自動的に小数第六位までになります。
以下はこれまでの課題を組み合わせて考える問題です。
必要であれば、交点の数は課題8では3個、課題9では4個であることを利用して構いません(利用しなくても作成することはできます)。流れとしては、
- 積分範囲を決めるために、交点を求める
- 求めた積分範囲で区分求積法を使って積分する
という流れになります。
これまでの課題の使えるところを組み合わせて、上手く計算してみてください。
課題8(応用問題)
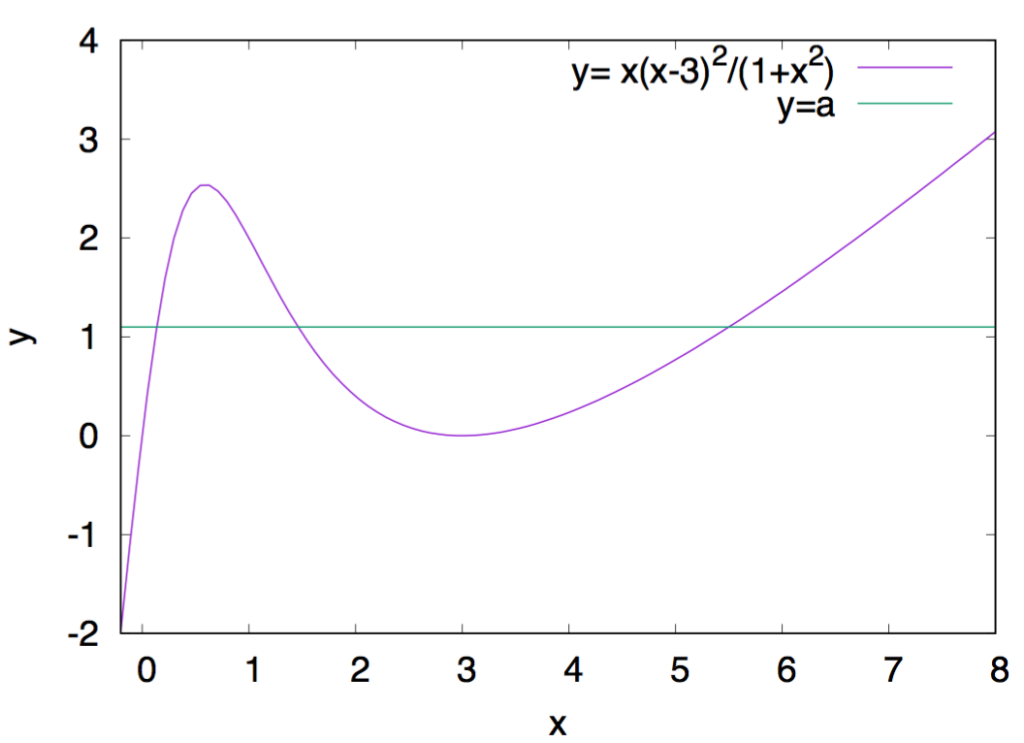
xy平面上の曲線,
![]()
と![]() の交点をそれぞれ
の交点をそれぞれ![]() とし、
とし、
![]() で二つの曲線で囲まれた領域の面積を
で二つの曲線で囲まれた領域の面積を![]() ,
,
![]() で二つの曲線で囲まれた領域の面積を
で二つの曲線で囲まれた領域の面積を![]() ,
,
二つの面積の合計を![]() とする。
とする。
![]() のときの
のときの![]() を求めるプログラムを作成せよ。
を求めるプログラムを作成せよ。
※ 交点は最大でも3つであることを利用しても良い。
課題9(応用問題)
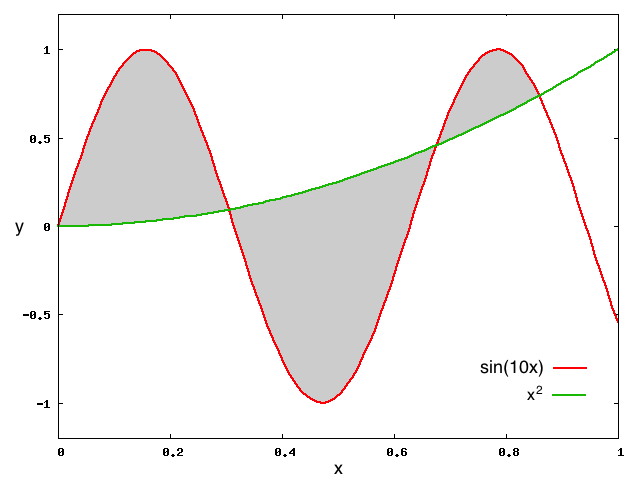
下図の灰色の部分の面積(の近似値)を数値的に求めるプログラムを作成せよ。
(曲線はそれぞれ y=sin(10*x), y=x*x)
ただし,分割後の領域の幅は0.001以下となるように分割数をとること。
(つまり積分する領域が[0,1]であれば1000分割以上すること)
※ 交点は最大でも4つであることを利用しても良い。
※ 得られる数値:0.519738程度であればOK。