コンテンツ
第5・6回(第3週)
グローバル変数とローカル変数
これまで関数と変数について習いました。ここでは、プログラム中での変数の定義の位置によって、変数の意味合いが変わることを見ていきましょう。 まずは基本となるプログラム(sample_global1.py)を考えましょう。
sample_global1.py
a = 10
print(f'a={a} in initial')
もはやこのプログラムの説明は不要でしょう。実行結果はa=10 in initialです。では次のような関数が含まれる場合(sample_global2.py)はどうでしょうか。
sample_global2.py
a = 10
def func1():
print(f'a={a} in func1')
print(f'a={a} in initial')
func1()
実行してみると、
a=10 in initial a=10 in func1
という結果が返ってきます。 計算数学演習でC言語を学習した人は「何故関数func1の中で、引数でもなく、定義もされていない変数aの値が得られるのだろうか?」という疑問を持つ人がいるかもしれません(疑問に思ってくれると助かります)。
C言語では、main関数で定義した変数の値を別の関数で使うには、引数として使うことを定義しなければならない、と教えました。一方、Pythonでは、このmain関数というものがありません(あるいは、1つのpythonプログラムそのものがmain関数という考え方もできますが)。
今回の変数aのように、関数の定義の外に定義している変数をグローバル変数といい、定義されている関数内でも参照することができます。では次のプログラム(sample_global3.py)はどうでしょうか?
sample_global3.py
a = 10
def func1():
print(f'a={a} in func1')
a = 20
print(f'a={a} in initial')
func1()
print(f'a={a} in final')
もしグローバル変数である変数aを関数内で読み書きすることできるのであれば、
a=10 in initial a=10 in func1 a=20 in final
という結果が返ってくることを期待するはずですが、残念ながらエラーが返ってくるはずです。 これは、「関数内で変数aの値の代入(書き換え)を伴っているため、変数aはグローバル変数ではない」と解釈されてしまうからです。このときの変数aは、ローカル変数といい、関数内でのみ利用可能な変数になってしまっています。そのため、sample_global3.pyのprint(f"a={a} in func1")の段階で、「変数aが定義されていないのに使われているよ!」とエラーがでるわけです。実際、次のプログラム(sample_global4.py)を実行すると、関数内での処理が終わった後は、さも代入などなかったかのように元の値に戻っています(正確にはそもそも変わっていないのですが…)。
sample_global4.py
a = 10
def func1():
a = 20
print(f'a={a} in func1')
print(f'a={a} in initial')
func1()
print(f'a={a} in final')
a=10 in initial a=20 in func1 a=10 in final
では、グローバル変数として関数内で変数aの値を変更するにはどうすれば良いのでしょうか?例えば次のプログラムのように関数内で変数aがグローバル変数であることを明示すれば良いでしょう。
sample_global5.py
a = 10
def func1():
global a
a = 20
print(f'a={a} in func1')
print(f'a={a} in initial')
func1()
print(f'a={a} in final')
global aによって、変数aがグローバル変数であることが宣言されています。
これらのプログラムを図的に表すと次のようなイメージです。
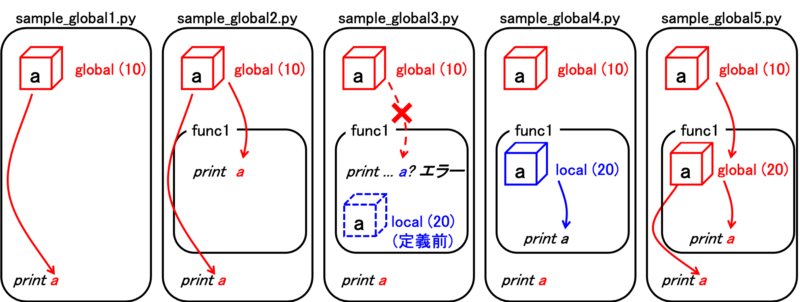
このように、グローバル変数とローカル変数という考え方を上手く使うと、効率的なプログラムを書くことができます。例えば、今後行うシミュレーションにおいて、定数パラメータをグローバル変数で定義すれば、いちいち引数などを使わなくても、プログラム全体で使用することができます。一方、広い範囲で使える、ということは、どこかで変更すると、その変更が他の部分に渡って反映されてしまう、ということでもあります。この場合、プログラムがこちらの想定外のところで予想と反した挙動をとるかもしれませんので、使用には注意が必要です。また、sample_global4.pyのように、同じ名前のグローバル変数とローカル変数が混在するようなプログラムも極力避けたほうが良いでしょう。
ちなみにC言語においてもグローバル変数を定義することができます。ヘッダーファイルなどのincludeが終わったあと(関数の定義の前)に変数を定義すれば、そのプログラム全体に渡って使うことができます。
常微分方程式の数値解法(オイラー法)
今回は次のような常微分方程式の初期値問題を、オイラー法と呼ばれる方法を用いて数値的に解いて結果をグラフにしてもらいます。 オイラー法は計算数学演習で扱っていますが、おさらいをしておきます。 次の問題を考えます。
(1) 
求めたいのは、![]() の範囲の
の範囲の![]() であり、関数
であり、関数![]() および定数
および定数![]() は与えられているとします。 また、
は与えられているとします。 また、![]() の値は
の値は![]() が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
コンピューターでは数値を離散的に(とびとびに)しか扱うことができません。 そこで、式(1)をコンピューターで扱えるようにする必要があります。 式(1)をコンピュータで解く方法には色々とありますが、今回は代表的なものの一つであるオイラー法を用います。
テイラー展開を使った導出
![]() について、時刻
について、時刻![]() から
から![]() だけ進んだ時刻
だけ進んだ時刻![]() における
における![]() について考えます。
について考えます。
テイラー展開を使うと
(2) 
と![]() の多項式で表現できます。ここで、
の多項式で表現できます。ここで、![]() 以上に関する項は、
以上に関する項は、![]() が十分小さいことを考えると、ランダウの記号
が十分小さいことを考えると、ランダウの記号![]() を用いて次のように表せます。
を用いて次のように表せます。
(3) ![]()
![]() は残りの項がおおよそ
は残りの項がおおよそ![]() に比例していることを示しています。今我々が考えている式(1)を使うと、
に比例していることを示しています。今我々が考えている式(1)を使うと、![]() ですので、
ですので、
(4) ![]()
となります。
ここで、![]() を無視した式を考えたいのですが、これまで考えていた
を無視した式を考えたいのですが、これまで考えていた![]() とは厳密には
とは厳密には![]() だけ異なるので、等号で表記するのは憚られます。そこで、数値計算解を
だけ異なるので、等号で表記するのは憚られます。そこで、数値計算解を![]() として表現すると、
として表現すると、
(5) ![]()
となります。この式がオイラー法の根幹となる次ステップの予測式になります。
ある時刻において![]() として、次のステップにおける誤差(局所誤差)を考えます。
として、次のステップにおける誤差(局所誤差)を考えます。
式(4)![]() 式(5)は
式(5)は
(6) ![]()
となります。すなわち、真の解![]() と数値解
と数値解![]() の間にはおおよそ
の間にはおおよそ![]() に比例した局所誤差が生じることを意味しています。局所誤差については、このあとのプログラムで実際に確認していきます。
に比例した局所誤差が生じることを意味しています。局所誤差については、このあとのプログラムで実際に確認していきます。
比較:差分商を用いた導出
高校までの微分の定義を使って導出することもできます。
ただし、この場合は誤差に関する議論はできませんので、注意が必要です。
![]() を
を![]() の関数としたとき、
の関数としたとき、![]() の
の![]() における微分係数は
における微分係数は
(7) ![]()
で定義されます。ここで、定義中の極限操作を取り払い、![]() を有限にとどめた
を有限にとどめた
(8) ![]()
を考えると、![]() を十分小さな値とすれば、式(8)は式(7)の近似となっていると考えられます。 この
を十分小さな値とすれば、式(8)は式(7)の近似となっていると考えられます。 この![]() のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、式(8)の右辺のような量を差分商といいます。 いまの場合は1階微分係数を近似する1階差分商です。
のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、式(8)の右辺のような量を差分商といいます。 いまの場合は1階微分係数を近似する1階差分商です。
では、このような差分商を用いて式(1)を離散化してみましょう。 まず、式(1)の第一式の微分係数を上記の差分商で置き換えてみます。
(9) ![]()
式(9)と式(1)の第一式は異なる方程式なので、式(1)の第一式の解 y(t) は一般に式(9)を満たしません。 そこで、混乱を防ぐために式(9)の![]() を
を![]() と書き換えましょう。すると、
と書き換えましょう。すると、
(10) ![]()
式(10)のように差分を含む方程式を差分方程式といいます。この式を整理すると、式(5)と同じ式を得ることができます。
帰納的解法
次に、式(1)の![]() を
を![]() に置き換えた初期条件
に置き換えた初期条件
(11) ![]()
の下で式(5)を解くことを考えます。式(5)に![]() を代入すると、
を代入すると、
(12) ![]()
となり、![]() から直ちに
から直ちに![]() が求まります。同様にして式(5)を繰り返し用いると、
が求まります。同様にして式(5)を繰り返し用いると、
(13) 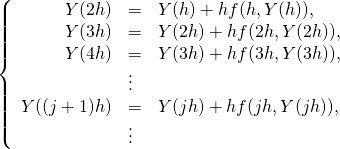
というように、![]() とすると帰納的に
とすると帰納的に![]() を
を![]() から計算できることがわかります。
から計算できることがわかります。
![]() をいったん決めると、
をいったん決めると、![]() 以外の時刻の
以外の時刻の![]() の値は式(??)からは求めることができません。 このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります。 そのようなとびとびの時刻を格子点と呼びます。
の値は式(??)からは求めることができません。 このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります。 そのようなとびとびの時刻を格子点と呼びます。 ![]() は格子点でのみ意味があるので、そのことを明示するために、
は格子点でのみ意味があるので、そのことを明示するために、![]() および
および![]() と数列で表現とすると、式(5)と初期条件は、
と数列で表現とすると、式(5)と初期条件は、
(14) ![]()
となり、結局式(1)の常微分方程式の初期値問題が、![]() に関する漸化式の問題式(14)に置き換えられました。この方法をオイラー法と呼びます。
に関する漸化式の問題式(14)に置き換えられました。この方法をオイラー法と呼びます。
ちなみに初期時刻![]() から開始し、時刻
から開始し、時刻![]() までの全区間にわたってオイラー法を行なった場合の
までの全区間にわたってオイラー法を行なった場合の![]() での誤差(大域誤差)は
での誤差(大域誤差)は
(15) 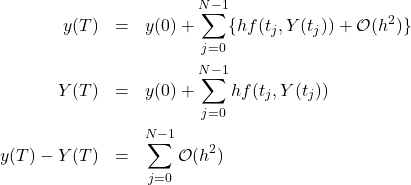
となります。
ところで今回の場合、![]() の正体は何だったか、というのを考えると、テイラー展開の2次以降の項をまとめたものであり、
の正体は何だったか、というのを考えると、テイラー展開の2次以降の項をまとめたものであり、![]() が十分小さいので局所誤差には
が十分小さいので局所誤差には![]() の項が効いてくるということでした。つまり、
の項が効いてくるということでした。つまり、
(16) 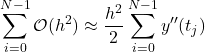
とかくことができます。
ここで、![]() のように算術平均を用意してあげれば、
のように算術平均を用意してあげれば、
(17) 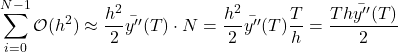
となり、大域誤差が![]() に比例することがわかります。
に比例することがわかります。
大域誤差と局所誤差の関係は、必ずしも1次違うわけではありません。アルゴリズムによっては2次以上違うものもあります。
1階常微分方程式に対するオイラー法のアルゴリズム
解を求める時刻の上限を![]() とし、与えられた時間刻み幅
とし、与えられた時間刻み幅![]() に対して、時間刻み数を
に対して、時間刻み数を![]() とします。
とします。
T, h, a 及び 関数 f は実数型(float)
N, j は整数型(int)
Y[N], t[N] は実数型配列(float)
T, h, aを設定
N = int(T/h)+1
N個の成分を持つ配列Y, tを用意する(インデックスは0..N-1)
Y[0] = a (初期条件の設定)
t[0] = 0
j = 0, 1, 2, ..., N-2の順に(for文)
t[j+1] = (j+1) * h
Y[j+1] = Y[j] + h * f(t[j], Y[j])
matplotlibを使ってグラフを描く
f(t,Y) は関数として定義するとよいでしょう。 ここではfor文の中でtの具体的な値を代入していますが、for文の外でt = np.linspace(0,T,N+1)としてももちろんOKです。
簡単な常微分方程式とその数値解のグラフ化
さて、実際にオイラー法をつかって常微分方程式を解いてみましょう。 次の常微分方程式を用いて演習を進めます。
(P) ![]()
前回(第3・4回)は、この微分方程式を解析的に解いて得られた解をグラフ化してもらいました。今回は式(P)をオイラー法を用いて数値計算で解いて、得られた数値解をグラフ化してもらいます。
課題1
(P)をオイラー法で解き、得られた数値解をグラフとして表示するプログラムを作成せよ。ただし、
![]()
とする。例えば次のようになる。 (この例では、![]() で時間刻み幅 h = 0.1 である。)
で時間刻み幅 h = 0.1 である。)
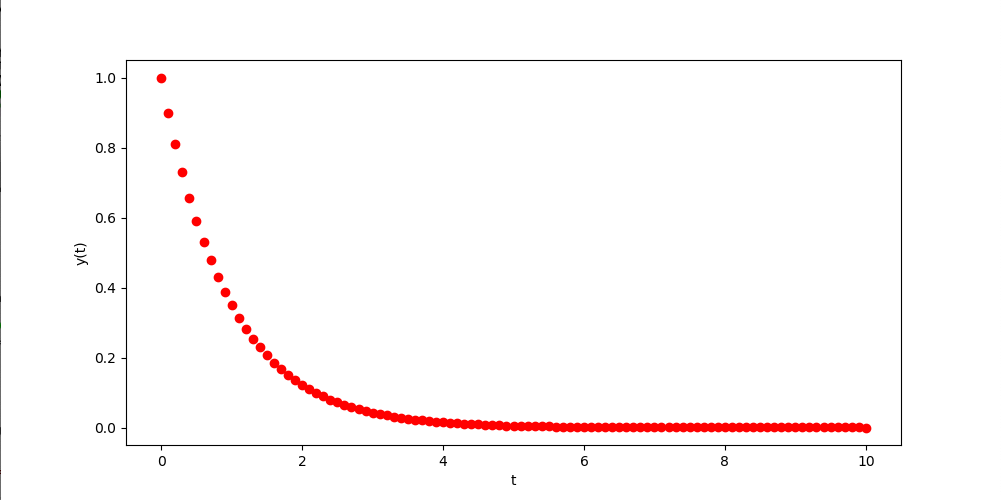
先週、解析的に求めた解をグラフとして表示したものは以下であるが、殆ど違いがない事に注意。 (課題2でみるが、微妙に異なっている)

課題2
前回解析的に求めた解(S)とオイラー法で求めた数値解を重ねて描くプログラムを作成せよ。 例えば、次のようになる。 この例では、解(S)を青色で描き、0≦t≦10で時間刻み幅h=0.5とした数値解を赤色で描いている。
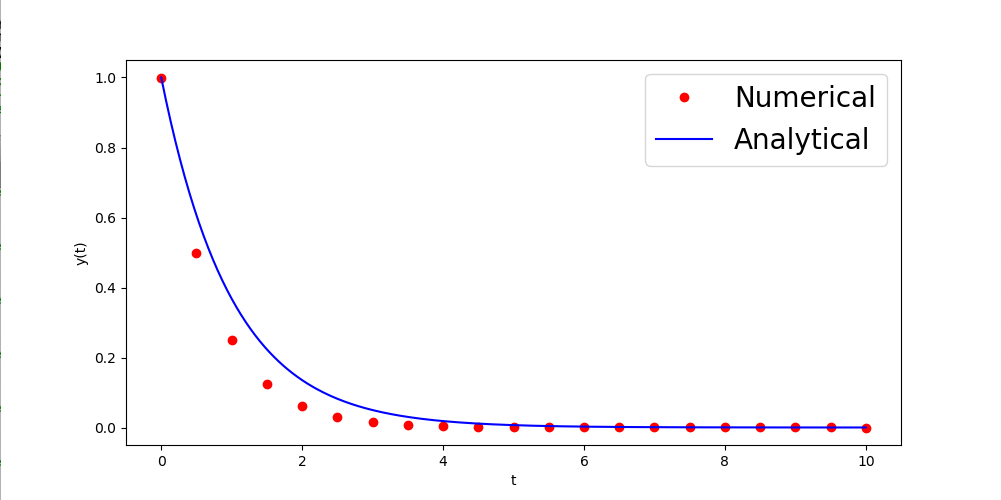
刻み幅を小さくすると両者の差は縮まる(すなわち真の解に近づく)。次の例では、時間刻み幅h=1/30としている。
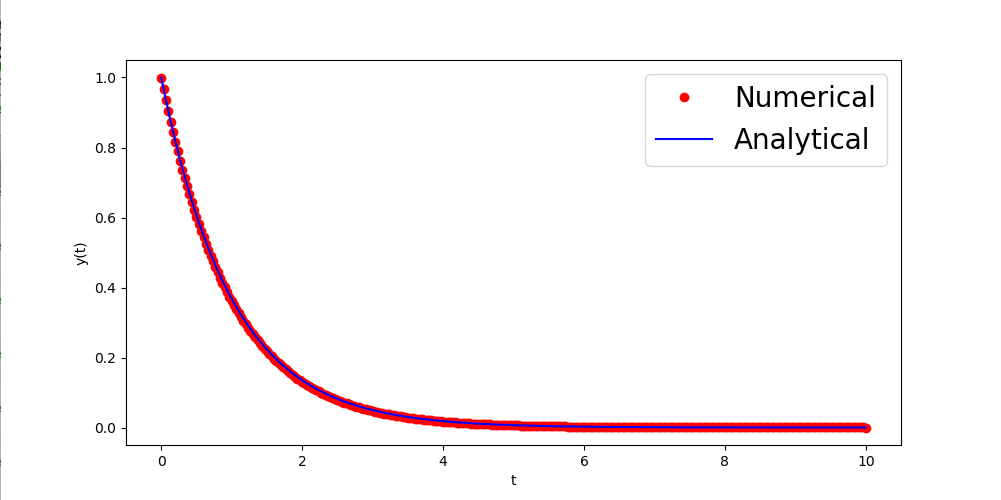
課題3
次の常微分方程式の初期値問題をオイラー法で解き、t と y の関係をグラフ化せよ。(次の小ネタも参照)
(1) ![]() (時刻 0≦ t ≦20 の範囲で時間刻み幅h=0.001、100ステップ毎に値を表示)
(時刻 0≦ t ≦20 の範囲で時間刻み幅h=0.001、100ステップ毎に値を表示)
(2) ![]() (時刻 0≦ t ≦20 の範囲で時間刻み幅h=0.001、50ステップ毎に値を表示)
(時刻 0≦ t ≦20 の範囲で時間刻み幅h=0.001、50ステップ毎に値を表示)
(3) ![]() もしくは
もしくは ![]() (時刻 0≦ t ≦20 の範囲で時間刻み幅0.001、100ステップ毎に値を表示)
(時刻 0≦ t ≦20 の範囲で時間刻み幅0.001、100ステップ毎に値を表示)
小ネタ:配列の要素を部分的に抜き出す
pythonの配列の便利さとして、次のような使い方ができます。
x = np.linspace(0,1,101) x[[0,4,6]] # 配列の0・4・6番目を抜き出す x[3:10:2] # 配列のうち3以上10未満の番号のものを2つ飛ばしで抜き出す x[:4] # 配列のうち4未満の番号のものを抜き出す x[4:] # 配列のうち4以上の番号のものを抜き出す x[4:-1] # 配列のうち4以上の番号でかつ最後でないものを抜き出す
これを使うと、必要以上にデータを描画したくないときに役に立ちます。
課題4
計算数学演習では、t や Y を配列ではなく変数で定義した(もちろん配列で定義する別解もあるが)。今回は、t や Y を配列で定義した。これは、Pythonでは配列があれば簡単にグラフ描画ができる、というのが大きな理由である。
配列を使った方がプログラミングは楽になる一方、Nがあまりにも大きくなるとメモリを食って動作が遅くなることがある。そこで、配列を使わない方法でオイラー法を実装し、課題1から課題3を解け。
レポート課題
課題2で作成したプログラムを少し変更して、 「λの値の入力を促し、そのλの値における解析解とオイラー法で求めた数値解を重ねて表示する」 プログラムを〇〇.py形式(名前は自由)で作成し、moodleから提出せよ。 ただし以下の点に注意すること。
- 初期値、t、yの表示範囲は課題2と同じ。
- 時間刻み幅h=0.001とすること。
- グラフの描画は100ステップに1回とすること。
- 数字や軸の名前が描いてあるかどうかも評価のポイント。
- 関数を作ってプログラムをシンプルに(読み易く)記述しているものは高く評価する。
- 適宜コメント文を入れること。
- プログラムの最初にコメントとして学生番号と氏名を必ず記述すること。 (# bxxxxxx 氏名)
提出期限2025年5月1日(木)0時00分
自由課題(上記の課題が終わった人へ)
セルオートマトン
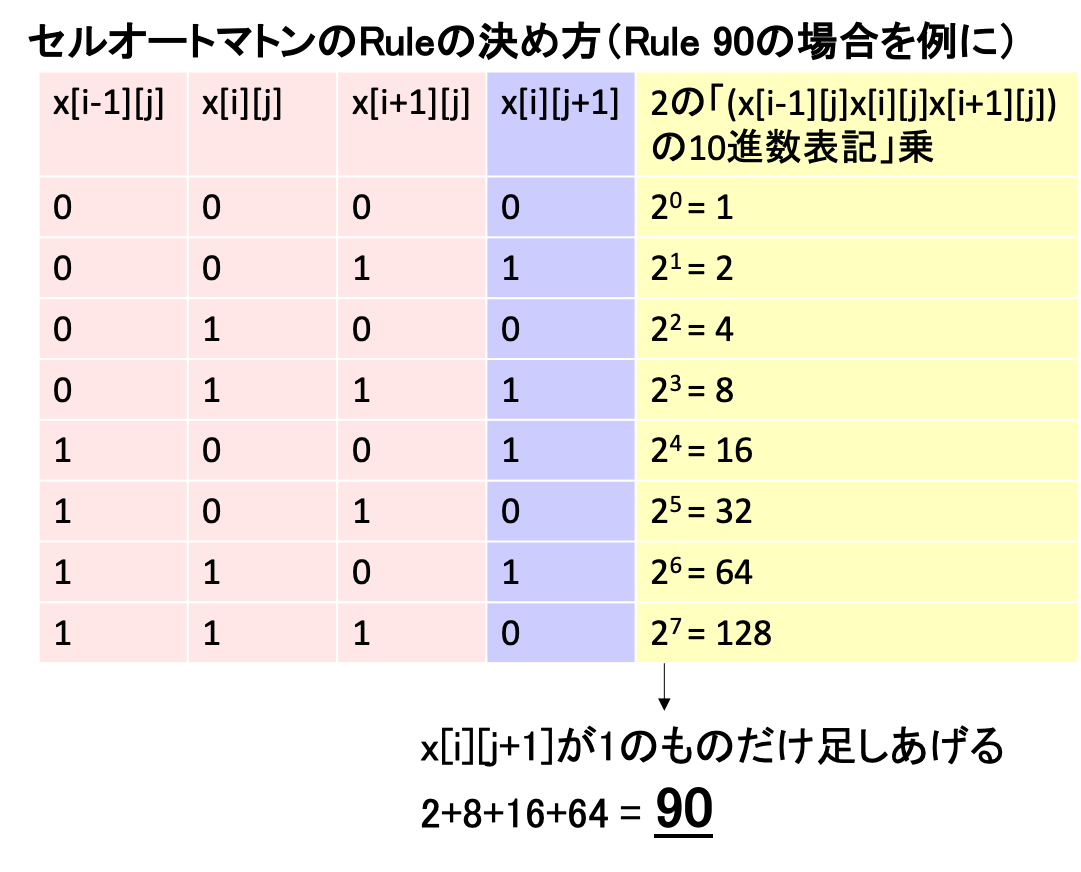
一次元セルオートマトンについて調べて描いてみてください。 ただし、ある時刻jのときの各セルiがもつ値x[i][j](0か1)は自分の値と両隣の値をもとに、次の時刻j+1の自分の値を決定する物とします。 (セルの数は自由に設定してください)
例としてRule90と呼ばれるもの以下に示します。 (iがセルの番号で、jが時刻を表すと思ってください)

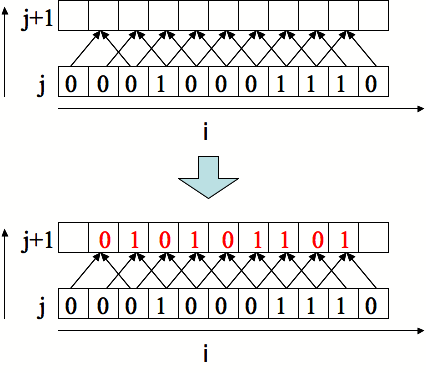
多次元配列を使っても良いですし、1次元配列を使っても良いです。1のところだけ●をつけると、次のような図が得られるはずです。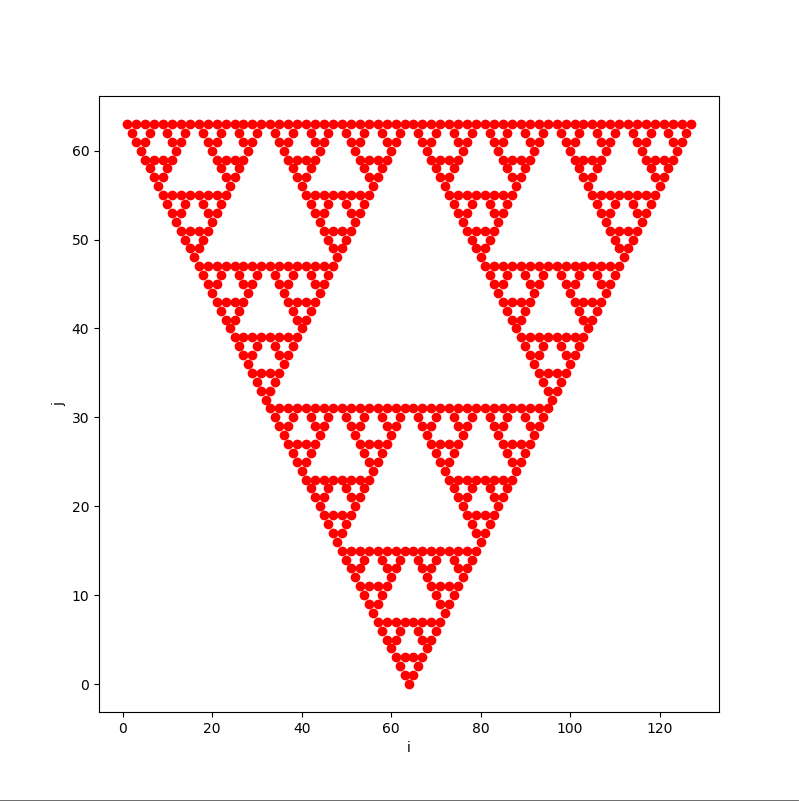
今回のように、(自分自身と)両隣のセルの値に応じて次のステップの値が決まるようなものを1次元3近傍系のセルオートマトンと言います。取りうる値の組合せは、3つのセルが2状態(0 or 1)を取るので、通りになります。それぞれの値の取り方によって、以下のような決まりによってRuleの番号が定められます。ちなみに藤井が個人的に好きなRuleは184です。(何故でしょう?)
講義で出てきた1階常微分方程式
いくつか講義で出てきた問題をあげておきます。 オイラー法で解いてみて、解をグラフとして表示してみてください。 初期値やパラメータを適当にきめて、いくつかシミュレーションしてみてください。
マルサスの式
(18) ![]()
ロジスティック方程式
(19) ![]()
2階常微分方程式の数値解法
2階常微分方程式もオイラー法を用いて解くことができます。 次の問題を考えて行きましょう。
(20) 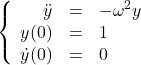
講義の説明の通り(下の枠中)、これは単振動を記述する2階の常微分方程式です。 ただし簡単の為、時間![]() での微分を
での微分を ![]() を用いてあらわしています。 バネ定数
を用いてあらわしています。 バネ定数![]() のバネの一端を固定し、他端に質量
のバネの一端を固定し、他端に質量![]() のおもりをつけた状況を考えます。
のおもりをつけた状況を考えます。
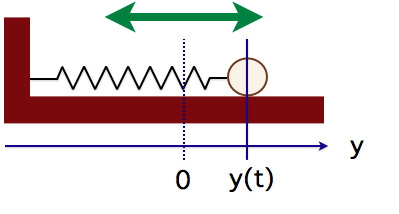
このおもりを少しだけ右に引っ張ってから手を放します。 おもりの中心の時刻![]() におけるつり合いの位置からのずれを
におけるつり合いの位置からのずれを![]() とすると、
とすると、![]() が満たす微分方程式は
が満たす微分方程式は
(21) ![]()
(22) ![]()
2階の常微分方程式は次のように連立の1階の常微分方程式に帰着できます。 ![]() とおくと、式(20)は、
とおくと、式(20)は、
(23) 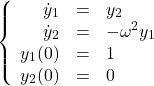
2階常微分方程式に対するオイラー法のアルゴリズム
解を求める時刻の上限を T とし、適当な自然数 N を定めて h=T/N とする。 T, h, a1, a2, y1, y2, y1_new, y2_new, t 及び 関数 f1, f2 は実数型 N, j は整数型
T,N,h を定める
配列y1[N+1], y2[N+1], t[N+1]を用意する
f1(t,y1,y2), f2(t,y1,y2) を関数として定義
y1[0] = a1, y2[0] = a2, t[0] = 0
j = 0,1,2,....,N-1の順に
t[j+1] = (j+1)*h
y1[j+1] = y1[j] + h*f1(t[j], y1[j], y2[j])
y2[j+1] = y2[j] + h*f2(t[j], y1[j], y2[j])
を繰り返す
matplotlibでグラフを描画
課題5
式(20)を解析的に解け。
課題6
![]() として式(23) をオイラー法で解き、グラフを描け。グラフは横軸が
として式(23) をオイラー法で解き、グラフを描け。グラフは横軸が![]() であり、縦軸を
であり、縦軸を![]() とせよ。 また、時間刻み幅
とせよ。 また、時間刻み幅![]() を変えたときに結果がどのようにかわるか観察せよ。 0≦t≦20の範囲において、h=0.0001,0.001, 0.01, 0.1それぞれの場合について、解析解とどの程度あっているか各自調べよ。
を変えたときに結果がどのようにかわるか観察せよ。 0≦t≦20の範囲において、h=0.0001,0.001, 0.01, 0.1それぞれの場合について、解析解とどの程度あっているか各自調べよ。
色々な h に対する計算結果は次のようになる(青はh=0.1、オレンジはh=0.01、緑はh=0.001、赤はh=0.0001のときの結果。紫は解析解のグラフ)。 この結果から、h は十分小さい値でないとまずいことがよく分かる。
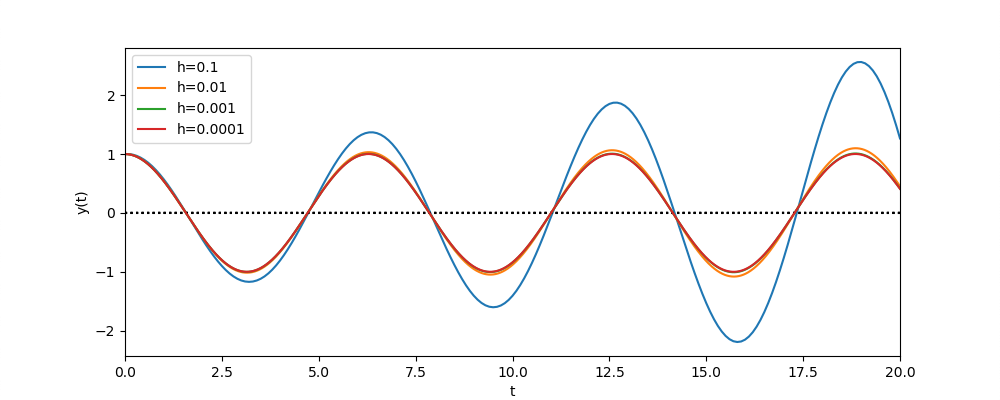
オイラー法では h を十分小さくとらないと本当の解をうまく近似できません。h を小さく取るということは、計算時間が多くかかることを意味します。そこでより高精度で大きな h でもうまく解を近似できるような解法が求められます。そのような要求に応える解法としては、ルンゲ・クッタ法があります。(計算数学演習でもやっていますが、次回改めて簡単に紹介します。)
課題7
(24) ![]()
課題8
実際のバネではバネの復元力以外におもりの速度![]() に比例する抵抗が働く。 その抵抗を考慮すると、式(20)ではなく次の式になる。(
に比例する抵抗が働く。 その抵抗を考慮すると、式(20)ではなく次の式になる。(![]() の項が新たに加わった。)
の項が新たに加わった。)
(25) 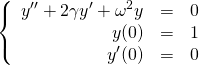
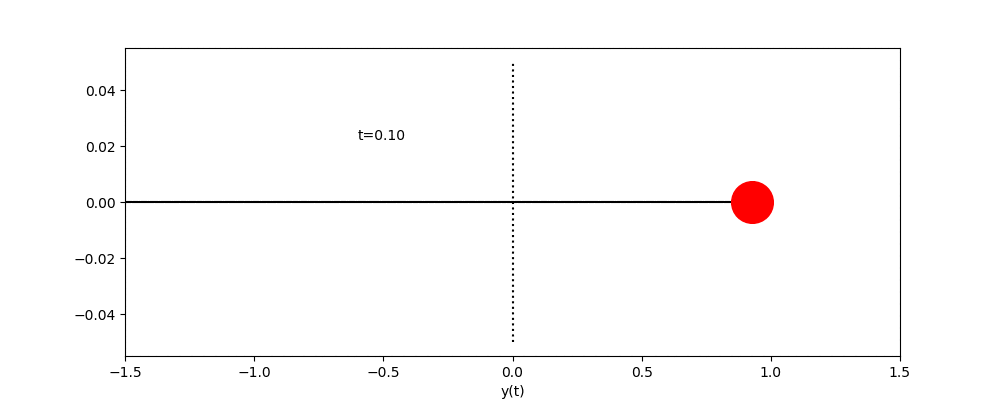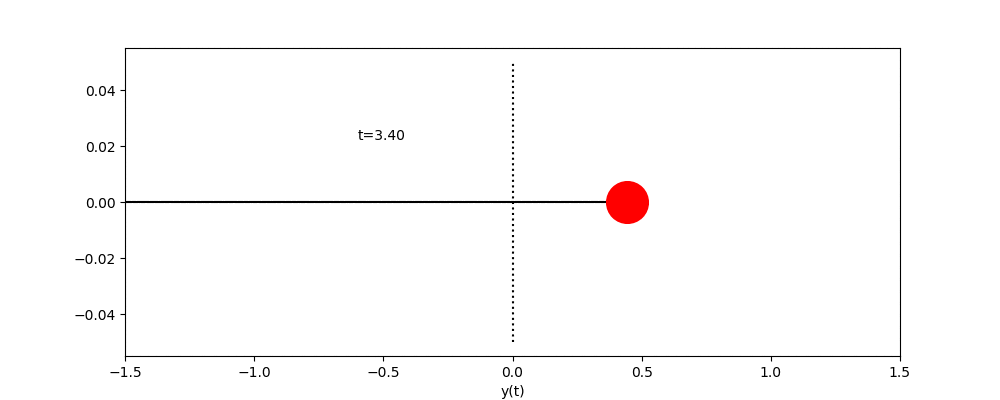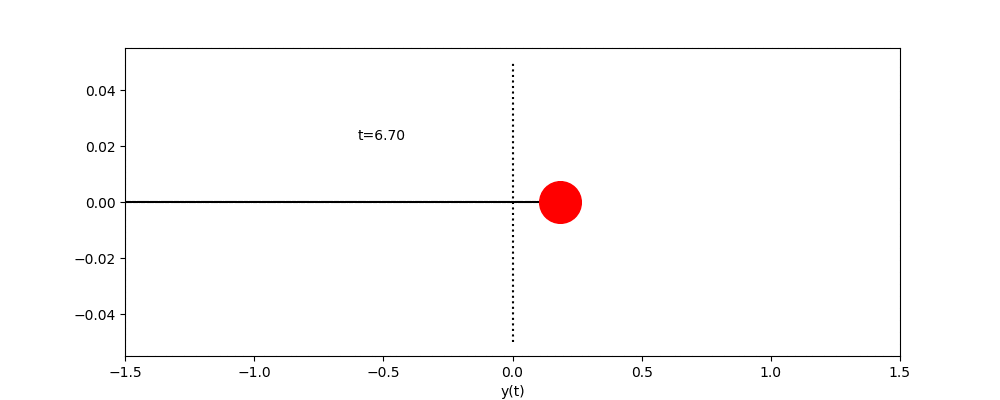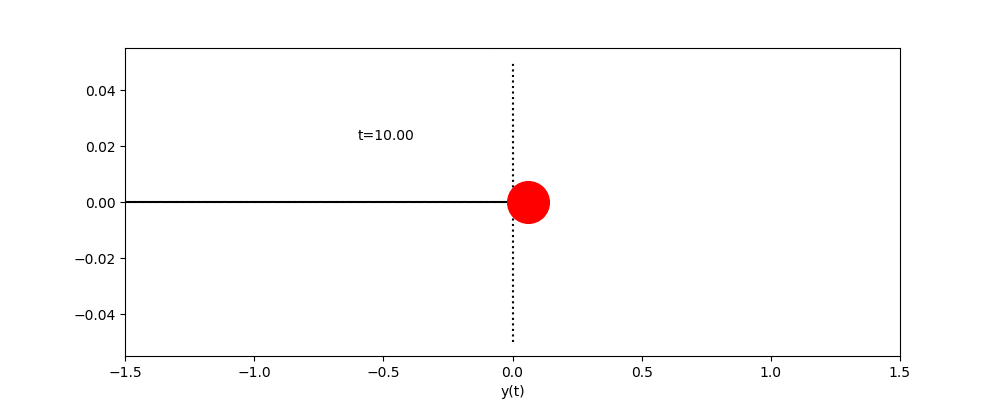
ただし、![]() とし、時間の刻み幅hは、0.01とする。また、左上の”t= ..”は現在の
とし、時間の刻み幅hは、0.01とする。また、左上の”t= ..”は現在の![]() を表示している。 デモプログラムでは、時間の刻み幅はh=0.01として、
を表示している。 デモプログラムでは、時間の刻み幅はh=0.01として、![]() まで計算している。
まで計算している。
今回は初めて微分方程式を解いてアニメーションを作成する、ということをやります。前回の資料も参考にしつつ、可能な限り自力で頑張ってみてください。どうしても無理!という人は、以下のリンク先に解答例を置いておきますので、参考にしてみてください(文字化けする場合は、テキストエンコーディングをUnicodeにするか、ダウンロードしてエディタで見てください)。
解答例1:逐次描画する場合(簡単、だけど重くなる)
解答例2:animation.ArtistAnimation関数を使う方法(推奨、ややコツが必要)
解答例3:animation.FuncAnimation関数を使う方法(トリッキーさが必要)
今後もこのようなアニメーションを作成するプログラムを作る機会が増え、レポートでも提出してもらうことが増えます。提出するプログラムでは、アニメーションの描画をが0.1動く毎におこなうようにしてください。(ヒント1: "%"をつかったif文) これは、無駄にプログラムの実行時間が長くなるのを防ぐためです。
“t=”の部分のアニメーションのさせ方:
他の点や棒の表記と同様にオブジェクトとしてテキストを作り、それをset_text関数を使って更新していきます。簡単な例は以下のようになります。
%matplotlib tk
import numpy
import matplotlib.pyplot as plt
T = 100
h = 0.01
fig = plt.figure()
ax = fig.add_subplot(111)
t = 0.0
txt = ax.text(0.3, 0.5, f"t={t:.2f}", transform=ax.transAxes)
for i in range(T):
t = i*h
txt.set_text(f"t={t:.2f}")
plt.pause(0.01)
課題9
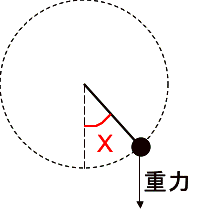
下図のような重力下で棒の長さ![]() が一定の振り子運動について考える。振り子の角度(ラジアン)
が一定の振り子運動について考える。振り子の角度(ラジアン)![]() は
は
(26) ![]()
という運動方程式を満たす(![]() は重力加速度、摩擦は無視しています)。
は重力加速度、摩擦は無視しています)。 ![]() として、この方程式を適当な初期条件、
として、この方程式を適当な初期条件、![]() でシミュレーションし振り子の動画を作成せよ。
でシミュレーションし振り子の動画を作成せよ。
今回の課題は、オイラー法では十分に小さい![]() を用いないと計算結果がすぐにずれてしまいますが、練習としてやってみてください。
を用いないと計算結果がすぐにずれてしまいますが、練習としてやってみてください。
次回、オイラー法より計算精度の高いルンゲ・クッタ法を紹介しますので、そのときに比較してみてください。
課題10
課題9の振り子が2つ相互作用する場合を考える. 例えば, 2つの振り子の角度を![]() とすると、
とすると、![]() が
が
(27) ![]()
という運動方程式を満たすとする。 この方程式を適当な ![]() と初期条件、
と初期条件、![]() でシミュレーションし、
でシミュレーションし、
(28) 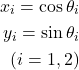
として振り子のアニメーションを作成せよ。また振り子の数をもっと多くした場合も考察せよ。