コンテンツ
オイラー法
今日の演習
- 1階常微分方程式の数値解法(オイラー法)
今日の目標
- 1階常微分方程式を解く方法を知る
常微分方程式の数値解法
次のような常微分方程式の初期値問題を、オイラー法を用いて数値的に解き、gnuplot を用いて結果をグラフにしてもらいます。
次の初期値問題を考えます。
(1) 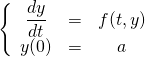
求めたいのは、![]() の範囲の関数
の範囲の関数![]() であり、関数
であり、関数![]() および定数
および定数![]() は与えられているとします。 また、
は与えられているとします。 また、![]() の値は
の値は![]() が与えられればいつでも計算できるものとします。 (プログラム中では関数として定義すると便利!)
が与えられればいつでも計算できるものとします。 (プログラム中では関数として定義すると便利!)
前回までのgnuplotでのグラフの描画と同様に、コンピューターでは数値を離散的に(とびとびに)しか扱うことができません。 そこで、式(1)をコンピューターで扱えるようにする必要があります。 式(1)をコンピュータで解く方法には色々とありますが、この演習では代表的なオイラー法(とルンゲ・クッタ法)を用います。
テイラー展開を使った導出
![]() について、時刻
について、時刻![]() から
から![]() だけ進んだ時刻
だけ進んだ時刻![]() における
における![]() について考えます。 テイラー展開を使うと
について考えます。 テイラー展開を使うと
(2) 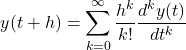
(3) ![]()
(4) ![]()
(5) ![]()
となります。この式がオイラー法の根幹となる次ステップの予測式になります。 ある時刻において![]() として、次のステップにおける誤差(局所誤差)を考えます。 式(4)
として、次のステップにおける誤差(局所誤差)を考えます。 式(4)![]() 式(5)は
式(5)は
(6) ![]()
比較:差分商を用いた導出
高校までの微分の定義を使って導出することもできます。 ただし、この場合は誤差に関する議論はできませんので、注意が必要です。 ![]() を
を![]() の関数としたとき、
の関数としたとき、![]() の
の![]() における微分係数は
における微分係数は
(7) ![]()
で定義されます。ここで、定義中の極限操作を取り払い、![]() を有限にとどめた
を有限にとどめた
(8) ![]()
を考えると、![]() を十分小さな値とすれば、式(8)は式(7)の近似となっていると考えられます。 この
を十分小さな値とすれば、式(8)は式(7)の近似となっていると考えられます。 この![]() のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、式(8)の右辺のような量を差分商といいます。 いまの場合は1階微分係数を近似する1階差分商です。
のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、式(8)の右辺のような量を差分商といいます。 いまの場合は1階微分係数を近似する1階差分商です。
では、このような差分商を用いて式(1)を離散化してみましょう。 まず、式(1)の第一式の微分係数を上記の差分商で置き換えてみます。
(9) ![]()
式(9)と式(1)の第一式は異なる方程式なので、式(1)の第一式の解 y(t) は一般に式(9)を満たしません。 そこで、混乱を防ぐために式(9)の![]() を
を![]() と書き換えましょう。すると、
と書き換えましょう。すると、
(10) ![]()
帰納的解法
次に、式(1)の![]() を
を![]() に置き換えた初期条件
に置き換えた初期条件
(11) ![]()
の下で式(5)を解くことを考えます。式(5)に![]() を代入すると、
を代入すると、
(12) ![]()
となり、![]() から直ちに
から直ちに![]() が求まります。同様にして式(5)を繰り返し用いると、
が求まります。同様にして式(5)を繰り返し用いると、
(13) 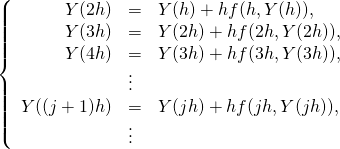
というように、![]() とすると帰納的に
とすると帰納的に![]() を
を![]() から計算できることがわかります。
から計算できることがわかります。
![]() をいったん決めると、
をいったん決めると、![]() 以外の時刻の
以外の時刻の![]() の値は式(5)からは求めることができません。 このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります。 そのようなとびとびの時刻を格子点と呼びます。
の値は式(5)からは求めることができません。 このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります。 そのようなとびとびの時刻を格子点と呼びます。 ![]() は格子点でのみ意味があるので、そのことを明示するために、
は格子点でのみ意味があるので、そのことを明示するために、![]() および
および![]() と数列で表現とすると、式(5)と初期条件は、
と数列で表現とすると、式(5)と初期条件は、
(14) ![]()
となり、結局式(1)の常微分方程式の初期値問題が、![]() に関する漸化式の問題式(14)に置き換えられました。この方法をオイラー法と呼びます。
に関する漸化式の問題式(14)に置き換えられました。この方法をオイラー法と呼びます。
オイラー法のアルゴリズム
以下では
(15) ![]()
#include <stdio.h>
double f(int, double); // 漸化式の右辺の定義
int main() {
int j, N = 20;
double Y = 1.0;
for (j = 0; j < N; j++) {
printf("%d %lf\n", j, Y); // Yの出力
Y = f(j, Y); // Y_{j+1} = f(Y_j)
}
return 0;
}
/* 漸化式の右辺 */
double f(int n, double Y) {
return 1 + 1.0/Y;
}
を用いてみましょう。
【注意】後々の説明のため、以下の点を変更しています。
-
-
- 独立変数:
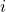 →
→ 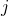
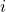 に対する従属変数:
に対する従属変数: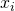 →
→ 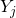
- 漸化式の右辺を関数 f で表現
- 独立変数:
-
漸化式のプログラムとオイラー法のプログラムで変更・追加しなければならないことを列挙します。 下の箇条書き先頭の【 】内に書かれている行番号は、この後に書かれているオイラー法のサンプルプログラム(euler.c)の行番号に対応しています。
- 【7, 8行目】解を求める時刻の上限を Tとし、適当な自然数 N (格子点の数。時間刻み数ともいう) を定める。
- 【9行目】時間刻み幅
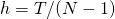 を定義
を定義 - 【8, 13行目】時刻
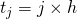 を定義(グラフを描くときの横軸になる。int型からdouble型になるので、諸々チェック!)
を定義(グラフを描くときの横軸になる。int型からdouble型になるので、諸々チェック!) - 【15, 22行目】漸化式を式(5)に変更(main関数の中と関数 f の中)
- 【10, 15, 16行目】(今後連立方程式を扱うことも念頭において)次の時刻での Y の値である Y_newを定義。
- 【16行目】for文の最後に、次の時刻のためにYをY_newで更新
次のサンプルプログラムは
![]()
オイラー法のサンプルプログラム:euler.c
#include <stdio.h>
double f(double, double); // 差分方程式の右辺の定義
#define a (1.0)
int main() {
int j, N = 100000;
double t, T = 10.0;
double h = T/(N-1);
double Y = a, Y_new;
for (j = 0; j < N; j++) {
t = j * h; // 現在の時刻
printf("%lf %lf\n", t, Y); // 現在のYの出力
Y_new = Y + h * f(t, Y); // Y_{j+1} = Y_j + h * f(t, Y_j)
Y = Y_new; // 次の時刻のためにYを更新
}
return 0;
}
/* 差分方程式の右辺 */
double f(double t, double Y) {
return -Y;
}
今後は、サンプルプログラムを陽には書かずに、以下のようなアルゴリズムで書くことが増えます。お決まりである#include <stdio.h>や変数の定義などが書かれておらず、またほとんど自然言語です。対応する制御構文や関数など、必要に応じて各自でアルゴリズムを元に、プログラミングしていく練習をしていきましょう。
例 euler.cのアルゴリズム
時刻の上限 T(下限は 0 ), 時間刻み数(格子点数) N を設定
時間刻み幅 h = T/(N-1) を設定
(ここから計算開始)
初期値を与える Y = 1
各格子点での値を j = 0,...,N-1 の順に計算 (for 文)
t = j*h // 現在の時刻
(一定間隔毎に)t と Y の値を画面に表示(printf関数)
Y_new = Y + h*f(t, Y)
次の時刻の計算のため、Y を新しく求まった値(Y_new)で置き換え
以上を繰り返す
オイラー法 あれこれ
#defineの利点と欠点・注意点
第9回で#defineの使い方を習いました。#defineを使うと、プログラム全体にわたる定数を1ヶ所で定義することができます。例えば上にあるeuler.cの場合、NやTおよびhなどはdefine文を使って次のように定義しても良いかもしれません。
euler2.c
#include <stdio.h>
#define N (100000)
#define T (10.0)
#define h (T/(N-1))
double f(double, double); // 差分方程式の右辺の定義
int main() {
int j;
double t;
double Y = 1.0, Y_new;
for (j = 0; j < N; j++) {
t = j * h; // 現在の時刻
printf("%lf %lf\n", t, Y); // 現在のYの出力
Y_new = Y + h * f(t, Y); // Y_{j+1} = Y_j + h * f(t, Y_j)
Y = Y_new; // 次のステップのためにYを更新
}
return 0;
}
/* 差分方程式の右辺 */
double f(double t, double Y) {
return -Y;
}
![]() のように、微分方程式に定数係数(ここでは
のように、微分方程式に定数係数(ここでは![]() )が含まれる場合も、#defineを使うと全ての関数に跨って定義できるため有用です。 一方、一度定義してしまうと、それ以降で値を変更することができなくなります。すなわち、例えば「実行の度にシミュレーション終了時間Tを入力する」場合には、#defineではなく通常の変数と同様にmain関数内で定義し、scanfで値を指定することが必要です。 また#defineでは、プログラムに含まれるトークン全てを変更してしまうため、上の例euler2.cの16行目
)が含まれる場合も、#defineを使うと全ての関数に跨って定義できるため有用です。 一方、一度定義してしまうと、それ以降で値を変更することができなくなります。すなわち、例えば「実行の度にシミュレーション終了時間Tを入力する」場合には、#defineではなく通常の変数と同様にmain関数内で定義し、scanfで値を指定することが必要です。 また#defineでは、プログラムに含まれるトークン全てを変更してしまうため、上の例euler2.cの16行目
Y_new = Y + h * f(t, Y);
では実際には
Y_new = Y + ((10.0)/((100000)-1)) * f(t, Y);
と置き換わっています。つまり、((10.0)/((100000)-1))と言う計算が毎回(無駄に)実行されていることになります。このような無駄な計算を省きたければ、やはりmain関数内で通常の変数として定義したほうが良いでしょう。 ※ 今回のような場合は大した無駄には思えないかもしれませんが、実際の研究ではもっと複雑で長いプログラムを実行する必要があり、このような無駄の積み重ねが命取りになりかねません。無駄計算をしていないか、注意しましょう。
時間と刻み数・刻み幅
上の例のeuler.cやeuler2.cでは、まず刻み数 N を定義し、次に時間の上限 T を定義し、最後にそれらから刻み幅 h を定義しています。一方、このようにまず刻み数 N の値を陽に定義し、刻み幅 h を間接的に決まるような方法は、科学研究にあまり向いていません。その理由として計算の精度があげられます。精度についての詳しい話は次回する予定ですが、ともかく、刻み幅 h を陽に決めるほうが一般的です。つまり、「時刻の上限Tと刻み幅 h を先に決め、刻み数 N を間接的に決める」というやり方や、「時刻の上限Tと刻み幅 h を先に決め、t = j*h > Tとなったら終了する」というやり方のほうが良いでしょう。 実際にどのようなプログラムになるか、各自で考えてみてください(課題2(4))。
一部分だけ出力
h が小さくなる(N が大きくなる)と、全ての j について t と Y_new を出力すると、結構なファイルサイズになり、PCに負担がかかります。そのため、出力する部分を以下のようなif文で囲むことで、○回に1回出力するようにできます (a % b = [a を b で割った時の余り])。
if (j % 100 == 0) {
printf("%lf %lf\n", t, Y);
}
この例では作成されるデータファイルの容量は1/100になります。 これは、第9回で見たように、グラフはある程度の折れ線数であれば十 分なめらかに見えるので、グラフを描く為のデータとして巨大になりすぎることを防ぐ為です。 ここで100という数値は適当に与えた物であって、グラフが十分なめらかに見えかつデータ数が小さくなるような適当な値を探す必要があります。(通常の連続なグラフであれば、グラフの点が200点くらいあれば十分滑らかに見えるでしょう。)
課題1
常微分方程式の初期値問題
![]() を解け。
を解け。
オイラー法を用いて 時刻 0≦ t ≦20 の範囲での解を求めるプログラムを作成せよ。 時刻 0≦ t ≦20 の範囲を20000等分割して(N = 20000)、100ステップ毎に printf関数により、t および y の値を表示し、それを gnuplot でグラフ化せよ。 また手計算にて解を求め、数値計算結果が正しいか確認せよ。
課題2
次の常微分方程式の初期値問題をオイラー法を用いて解いて、![]() と
と![]() の関係を gnuplot でグラフ化せよ。
の関係を gnuplot でグラフ化せよ。
(1)![]() (時刻 0≦ t ≦2 の範囲を20000等分割、100ステップ毎に値を表示)
(時刻 0≦ t ≦2 の範囲を20000等分割、100ステップ毎に値を表示)
(2)![]() (時刻 0≦ t ≦20 の範囲を20000等分割、100ステップ毎に値を表示)
(時刻 0≦ t ≦20 の範囲を20000等分割、100ステップ毎に値を表示)
(3)![]() (時刻 0≦ t ≦10 の範囲を10000等分割、100ステップ毎に値を表示)
(時刻 0≦ t ≦10 の範囲を10000等分割、100ステップ毎に値を表示)
(4)![]() もしくは
もしくは ![]() (時刻 0≦ t ≦20 の範囲で時間刻み幅h=0.001、100ステップ毎に値を表示)
(時刻 0≦ t ≦20 の範囲で時間刻み幅h=0.001、100ステップ毎に値を表示)
※ (4)はhを先に定め、TとhからNを計算する方式にしてください。
今日学んだ事
- オイラー法による常微分方程式に数値解法