コンテンツ
第11回
1次元拡散方程式の数値解法(その2)
次の問題を考えます。先週の問題1.1と少し違いますので注意してください(初期値と x の範囲が異なる)。
問題1.2
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \left\{ \begin{array}{lc} \frac{\partial u(x, t)}{\partial t} = D\frac{\partial^2u(x, t)}{\partial x^2} & (x \in (0, \pi), t> 0) \\ u(0, t) = 0 & (t>0) \\ u(\pi, t) = 0 & (t>0) \\ u(x, 0) = \sin(x) + \sin(7x) & ( x \in [0, \pi] ) \end{array} \right. \end{equation*}](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-46e1a5a6fa672aceaa5ee70db37b5bf2_l3.png)
課題1
問題1.2の解を数値的に求めるプログラムを作成せよ。
問題1.2の数値計算結果例
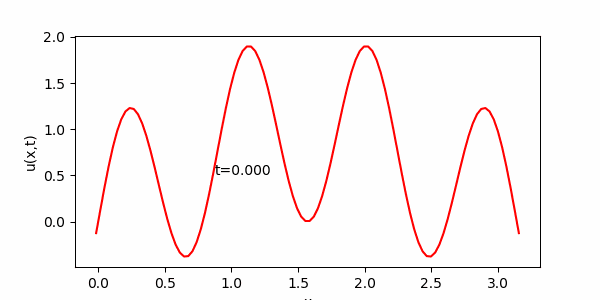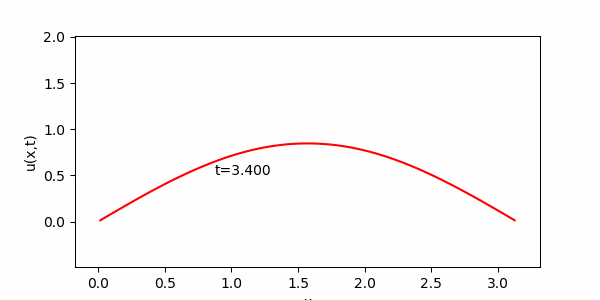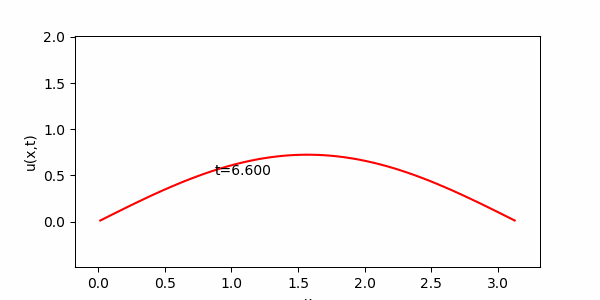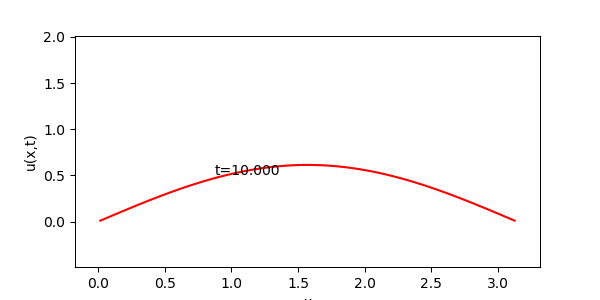
※ 上のアニメーションでは![]() としている。
としている。
課題2
(初期値のsinの部分をcosに書き換えて)境界条件をノイマン条件に変更すると、どのような振る舞いをするか調べよ。
ノイマン条件にするには、式(4)の代わりに
![]()
とすればよい。
先に出てきた、
![]()
を繰り返し計算し、近似解を求める方法を陽解法と呼びます。
(前の時刻![]() での値から次の時刻
での値から次の時刻![]() の値を直ちに計算できる形の差分方程式を陽公式(explicit scheme)と呼びます。陽公式を使った解法なので陽解法と呼びます。)
の値を直ちに計算できる形の差分方程式を陽公式(explicit scheme)と呼びます。陽公式を使った解法なので陽解法と呼びます。)
天下り的になりますが、拡散方程式の数値解法として陽公式を用いる場合、![]() と
と![]() と
と![]() は次の関係を満たす必要があります(安定性条件)。
は次の関係を満たす必要があります(安定性条件)。
(S) ![]()
ここでは、この安定性条件を破った場合に計算がどのようになるかを見ます。
安定性条件の導出は、フーリエ級数展開を用いたノイマンの安定性解析法を用います。ノイマン法を用いると、各周波数の振幅に関する常微分方程式が現れます。これを解いて、振幅が収束するか、発散するか議論すれば良いわけです。詳しくは講義で紹介されます。
課題3
課題1のプログラムにおいてのパラメータ N (空間刻み数)やパラメータ M (時間刻み数) 等を調節し、安定性条件(S)をわずかに破ってみよ。
課 題3に従い、安定性条件(S)をわずかに破った場合、次のような結果が得られます。
(S)の左辺の値が 0.51 と、1/2 をわずかに越えているにすぎませんが、最終的には真の解からはほど遠いギザギザの状態になってしまいます。
1/2 を大きく越えると、計算がおかしくなるのも早まります。
(ここではD をα>1/2 となるように調整した。)
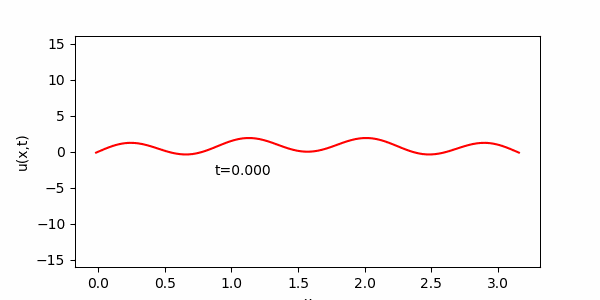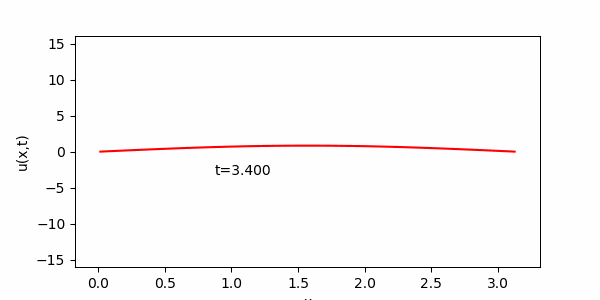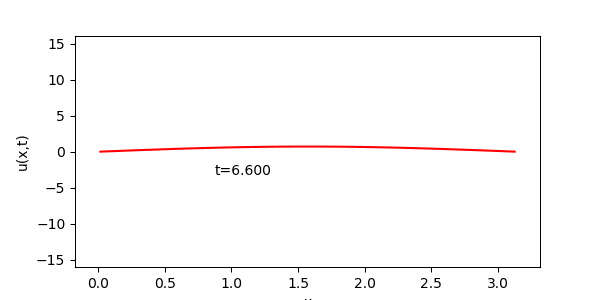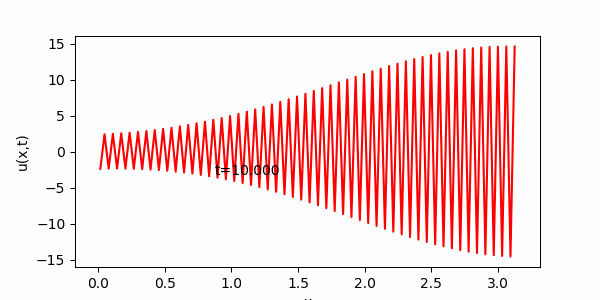
上 の、ギザギザの解は、直感的に考えても熱方程式の解としてはおかしいことがわかると思います。(スプーンの熱分布がこの様になるとは思えません。)
陽解法においては安定性条件を満たさないパラメータで計算すると、計算が不安定となり、上記のような現象が見られます。
(ただし、これは、「差分方程式の解としては」正しいものです。しかし、近似したい熱方程式の近似解とはなっていところが問題なのです。)
注意:上の計算結果では対称性の崩れ(初期値は π/2 で対称)がみられます。これは、πを近似値として与えたためであると思われます。
この様に、陽解法においては、計算が安定に進むためには時間刻み幅および空間刻み幅が安定性条件(S)を満たさねばなりません。
ところが、この条件は計算量の点で問題があります。
例えば、時刻0から1まで計算を行うとします。
時間方向の格子点の総数は 1/τとなります。
計算の手間(計算時間)を減らす為には τ をなるべく大きく取りたい(τ が大きければ少ない繰り返し計算で目的の時刻まで計算できるので)。
そこで、安定性条件(S)より、
τ ≒ h2/(2D)
とすれば良いでしょう((S)を余裕をもって満たす τ を用いる)。
一方、D は一定とした場合、精度の良い計算をするために空間に関する分解能を高めたいとします。
そこで h を 1/10 倍にしたとします。すると、τ は上の関係から 1/100 倍せざるを得ません。
ということは、時間方向の格子点数が 100倍 に増えることになります。
これでは、 h を小さくしていったときに、あまりに格子点数が多くなりすぎて計算の効率が悪くなります。
例えば今の例では、h を 1/10 倍したため、計算量は 10 倍となり(これは仕方が無い)、また、安定性条件(S)を満たすために τ を 1/100 倍したのでその分計算量は100倍となりました。
つまり、もとの計算量に比べて 1000倍の計算量が必要(1000倍時間がかかる!)となります。
つまり、陽解法では、空間解像度を細かくしたい場合に、時間刻み幅もそれにあわせて変更する必要があります。
できることならそういう事を気にせずに(全く気にしなくても良いわけではありませんが・・)自由に空間解像度を上げ下げしたいものです。
その要求を満たす解法として陰解法と呼ばれる方法があり、陰解法は無条件安定であることがわかっています(安定な計算に対するαに関する条件が無い)。
(演習では時間の関係から陰解法についてはできませんが、各人陰解法のプログラムの作成をしてみることをおすすめします。陰解法では連立一次方程式を解く必要がありますが、それらのプログラムは良いプログラミングの練習にもなります。)
レポート課題
次の特殊な境界条件下での拡散方程式について、
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \left\{ \begin{array}{lc} \frac{\partial u(x, t)}{\partial t} = D\frac{\partial^2u(x, t)}{\partial x^2} & (x \in (0, \pi), t \in (0,2)) \\ u(x, 0) = \frac{A}{2}(\cos(x) + \cos(7x)) & ( x \in [0, \pi] ) \\ u(0, t) = A, \frac{\partial u(\pi, t)}{\partial x} = 0 \end{array} \right. \end{equation*}](https://home.hiroshima-u.ac.jp/~mafujii/wordpress/wp-content/ql-cache/quicklatex.com-ce0bb6f2f5badf7effa1b02378d64dc3_l3.png)
拡散係数![]() を
を![]() と三つの異なる場合について、同時にアニメーションに描画するpythonプログラムを作成し、moodleから提出して下さい。
と三つの異なる場合について、同時にアニメーションに描画するpythonプログラムを作成し、moodleから提出して下さい。
ただし、以下の点に注意すること
- t=0から2.0までのアニメーション
- A=1として、時刻tもwindow内に表示。
- 異なる拡散係数を同時に表示するので、安定性条件に留意してすべての場合で計算が破綻しないように適切なパラメータを選択すること。
- また、色の違いで拡散係数の違う拡散方程式の解を表示し、その情報も載せること。
採点基準はこれまで同様、コードの可読性、アニメーションの表示方法、必要要件の有無が採点対象となります。
インデント(時下げ)、コメントは必ず行うこと。
また、プログラムの最初の方にコメントとして学生番号と氏名は(最低限)必ず記述すること。
(# bxxxxxx 氏名)
提出期限:2025年5月28日(水)23時59分
実行例
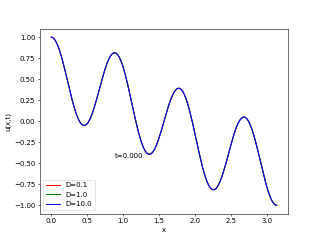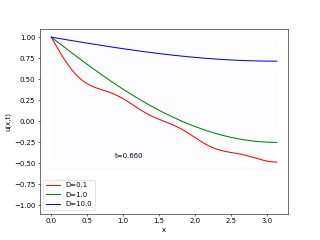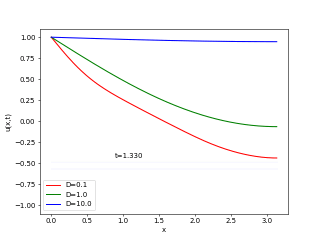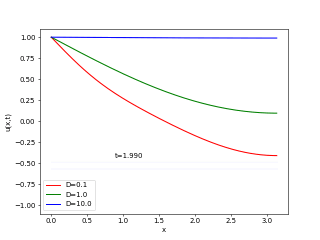
おまけ1(反応拡散系の初歩)
拡散方程式は偏微分方程式のごくごく一部です。
右辺に拡散だけでなく、新たに関数![]() を加えたものを考えてみましょう。
を加えたものを考えてみましょう。
(3) ![]()
今、![]() の部分は任意です。
の部分は任意です。
![]() や各種条件とパラメータを以下のようにしてみましょう。
や各種条件とパラメータを以下のようにしてみましょう。
(4) 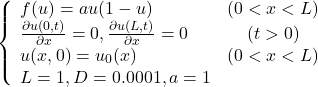
このとき初期条件を
(5) ![]()
とし、適当な![]() について振る舞いを調べてみてください。また、
について振る舞いを調べてみてください。また、![]() を変えた際、
を変えた際、![]() の値に応じて、解の振る舞いがどのように変化するか調べてみましょう。以下の動画では、時間刻み
の値に応じて、解の振る舞いがどのように変化するか調べてみましょう。以下の動画では、時間刻み![]() 、空間刻み
、空間刻み![]() とし、
とし、![]() が0.1増える毎に描画しています。
が0.1増える毎に描画しています。
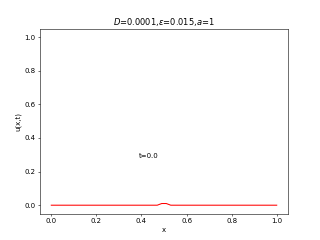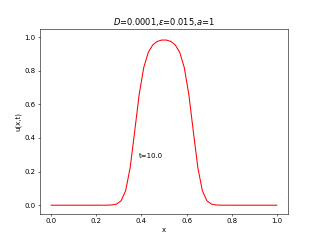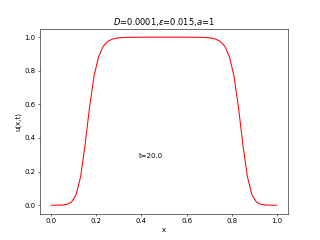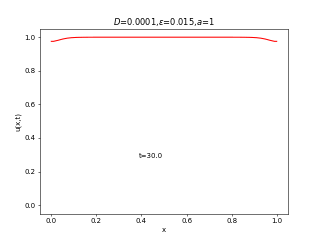
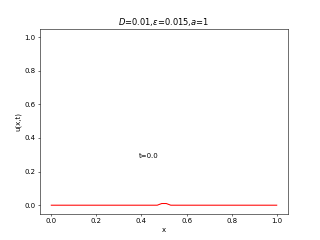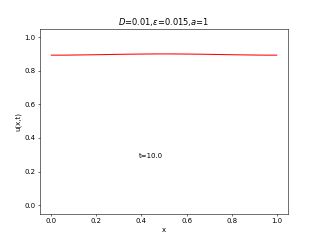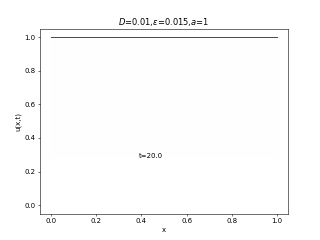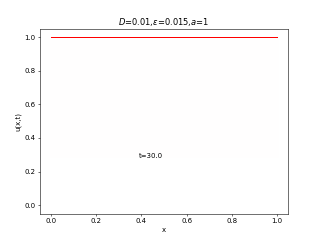
実は先端数学の藤井の回の最初に出てきた反応拡散系の式はこの式です。右辺にロジスティック方程式と同じがつくだけで、全然異なる振る舞いを見せます。ロジスティック方程式は人口増加のモデルであったことを思い出すと、
が小さい(移動度が低い)場合は人口増加によって局所的に繁栄したのちに領土を広げていくのに対して、
が大きい(移動度が高い)場合は全体的に領土を広げたのちに、人口増加していく様子が見えると思います。
おまけ2(2変数の反応拡散系)
今まで拡散方程式は![]() についてのみ考えてきましたが、当然ながら多変数のものを考えることもできます。
についてのみ考えてきましたが、当然ながら多変数のものを考えることもできます。
(6) 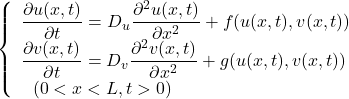
具体例として、![]() に次の式を入れてみましょう。
に次の式を入れてみましょう。
(7) ![]()
拡散がなければ、神経発火のモデルとして有名なFitzhugh-Nagumo方程式と呼ばれるもので、パラメータによっては振動や興奮性を示したり1点に収束するような方程式です(式やパラメータ表記などはいくつかありますが、性質としては変わりないです)。
(8) 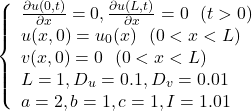
とし、
(9) ![]()
としてシミュレーションしてみてください。パラメータによって振る舞いが変わります。非一様な初期値からスタートすれば、だいたい同じような形にたどり着きます。
このような安定な解に落ち着いたと見せかけて波のようなパターンが出てくることは、「チューリング不安定性」によって説明できます。計算数理Aの講義で、フーリエ級数展開した解を拡散方程式に代入し、各波数の収束速度を確認したと思いますが、同様の方法でこの不安定化を説明することができます。(おそらく今後の応用系の授業で出てくると思います。)