オイラー法２

今日の演習

• 2階常微分方程式の数値解法（オイラー法）
• ルンゲクッタ法
  

（復習）オイラー法による２階常微分方程式解法

つづいて、２階常微分方程式をオイラー法を用いて解いてもらいます．次の問題を考えます．

　

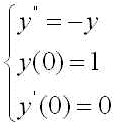  （１1）

これは単振動を記述する２階の常微分方程式です．ただし簡単の為、時間 t での微分を ' を用いてあらわしています．２階の常微分方程式は次のように連立の１階の常微分方程式に帰着できます．y1(t)=y(t), y2(t)=y'(t) とおくと、（１１）式は

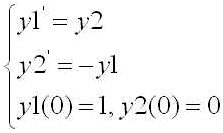  （1２）

となります．もう少し一般的な書き方をすれば

　y1' = f1(t, y1, y2)　（今回は f1(t, y1, y2) = y2）

　y2' = f2(t, y1, y2)　（今回は f2(t, y1, y2) = -y1）

という形になります. こうなれば先程と同様、オイラー法を用いて解を求めることができます． アルゴリズムは次のようになります．

ただし、

T を解を求める時刻の上限 (下限 ０) とし、N を時間刻み数、h = T/(N-1) を時間刻み幅とします.

変数は y1, y2 として、a1, a2 を初期値とします．

（１２）式の第一式の右辺を f1(t, y1, y2), 第二式の右辺を f2(t, y1, y2) とそれぞれ定義します.

オイラー法のアルゴリズム

T, h, a1, a2, y1, y2, y1_new, y2_new, t（時刻） 及び 関数 f1, f2 は実数型(floatまたはdouble)

N, j は整数型(int)

T,N,h を定める

y1 = a1, y2 = a2

初期時刻0と初期値a1, a2を画面に表示（printf関数）

j = 0,1,2,....,N-1の順に

    t = j*h

    y1_new = y1 + h*f1(t, y1, y2)

    y2_new = y2 + h*f2(t, y1, y2)

    一定間隔毎t+h, y1_new, y2_new を画面に表示（printf関数）

    y1 = y1_new

    y2 = y2_new

を繰り返す

f1(t, y1, y2)、 f2(t, y1, y2) は関数として定義するとよい．

注意

各ステップで, y1_new, y2_new が両方求まってから y1 = y1_new, y2 = y2_new と値を更新するようにします. ここの順序が変わってくると, y1 と y2 で時間がずれてしまうので, 正確な計算になりません.

オイラー法では h を十分小さくとらないと本当の解をうまく近似できません．h を小さく取るということは、計算時間が多くかかることを意味します．そこでより高精度で大きな h でもうまく解を近似できるような解法が求められます．そのような要求に応えるルンゲ・クッタ法があります(次に触れます)．

課題１

次の微分方程式

dy/dt = v

dv/dt = - 0.1*v - y + A*cos(B*t)

を、初期値y=1, v=0のもと数値的に解き B = 0,0.5,1,2 の場合の y の時間変化を調べて下さい(時刻の上限を少し大きめにして下さい.)．また、y と v の関係（gnuplot で横軸を y, 縦軸を v として）も plot してみて下さい. これは摩擦抵抗のあるバネ振動子に、周期的な外力を加えたもので、強制振動系と呼ばれます

 

以下、オイラー法より計算精度の高い、ルンゲ・クッタ法について紹介します。興味のある方は参考にしてください. 期末レポートの計算や以下の課題の幾つかは、オイラー法, ルンゲ・クッタ法, 何れを方法を用いても可能ですので、ここを飛ばして課題４以降に進んでも構いません.

ルンゲ・クッタ法（次回にしっかり取り扱います）

これまでオイラー法を 用いた数値解法の演習を行いました．オイラー法は単純でそれはそれでよいのですが、実際の解に近い数値解を出すためには、時間刻み幅 h をかなり小さくとらねばならないことが前回の課題等によってわかります．そこで、より精度の高い解法が必要となりますが、今回はそのような解法として、ルンゲ・クッタ法を扱い、それを用いた数値解法の演習を行います．

ルンゲ・クッタ法の導出については、このページの最後を参照してください（詳細は参考書を参照してください）．ルンゲ・クッタ法は次にしめすようなアルゴリズムで、オイラー法に比べれば多少複雑なものとなっています（赤字で示したところが一階微分方程式に関するオイラー法からの変更箇所です.）．

（一階常微分方程式に対する ルンゲ・クッタ法）

T を解を求める時刻の上限とし、h を時間刻み幅、N を時間刻み数とします．また、変数は y とし、a を初期値とします．r1, r2, r3, r4 はそれぞれ実数型の変数です．

T,N を設定 (#define 文）

初期値 a を設定 (#define 文）

h を定める

y = a

t = 0 での y の値の表示 (printf 関数)

j = 0,1,2,....,N-1の順に

    t = j*h

(以下, t, y から y_new を求めるのに, 計算精度を上げるためやや遠回りをします. 具体的には t, y から r1 を求め, t, y, r1 から r2 を求め, ... t, y, r3 から r4 を求め, 最後に　y, r1, r2, r3, r4 から y_new を求める. この遠回りのおかげで、計算精度が非常に良くなります. )

    r1 = f(t, y)

    r2 = f(t + h/2, y + (h/2)*r1)

    r3 = f(t + h/2, y + (h/2)*r2)

    r4 = f(t + h, y + h*r3)

    y_new = y + (h/6)*(r1 + 2*r2 + 2*r3 + r4)

    y = y_new

    (一定間隔毎に)t+h と y_new の表示 (printf関数)

を繰り返す

（二階常微分方程式に対する ルンゲ・クッタ法）

先の課題で扱った

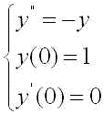  （１）

をy1(t)=y(t), y2(t)=y'(t) とおいて次のように連立の１階の常微分方程式に帰着したもの

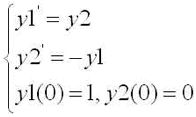  （２）

を再び考えます(y'' は y の時間に関する２階微分)．このような連立の常微分方程式をルンゲ･クッタ法を用いて解く場合のアルゴリズムを次に示します．（赤字で示したところが二階微分方程式に関するオイラー法からの変更箇所です.）

ただし、

T を解を求める時間の上限とし、h を時間刻み幅、N を時間刻み数とする.

変数は y1, y2 とし、それぞれの初期値を a1, a2 とします．r11, r21, r31, r41, r12, r22, r32, r42 および y1_new, y2_new はそれぞれ実数型の変数とする．

f1(t, y1, y2) および f2(t, y1, y2) はそれぞれ実数型の関数で（２）式の場合には f1 が第一式の右辺、 f2 が第二式の右辺となります．

T,N を設定 (#define 文）

初期値 a1, a2 を設定 (#define 文）

h を定める

y1 = a1

y2 = a2

t = 0 での y1, y2 の表示 (printf 関数)

i = 0,1,2,....,N-1の順に

   t = i*h

    r11 = f1(t, y1, y2)

    r12 = f2(t, y1, y2)

    r21 = f1(t + h/2, y1 + (h/2)*r11, y2 + (h/2)*r12)

    r22 = f2(t + h/2, y1 + (h/2)*r11, y2 + (h/2)*r12)

    r31 = f1(t + h/2, y1 + (h/2)*r21, y2 + (h/2)*r22)

    r32 = f2(t + h/2, y1 + (h/2)*r21, y2 + (h/2)*r22)

    r41 = f1(t + h, y1 + h*r31, y2 + h*r32)

    r42 = f2(t + h, y1 + h*r31, y2 + h*r32)

    y1_new = y1 + (h/6)*(r11 + 2*r21 + 2*r31 + r41)

    y2_new = y2 + (h/6)*(r12 + 2*r22 + 2*r32 + r42)

    y1 = y1_new

    y2 = y2_new

    (一定間隔毎に) t+h と y1_new, y2_new を画面に表示 (printf関数)

を繰り返す

 

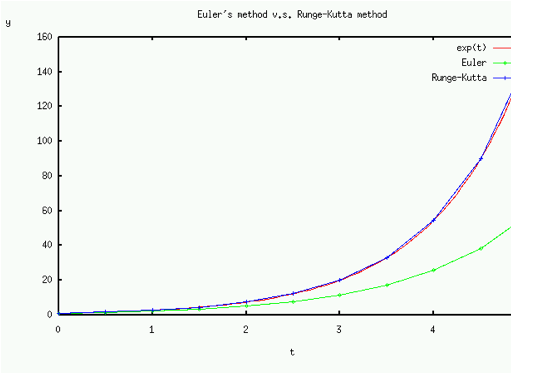
練習課題

上記のルンゲ･クッタ法を用いて、次の問題を実際に解き、ルンゲ･クッタ法がオイラー法と比べてどの程度性能が良いか比べよ．次の初期値問題を 時刻 0≦t≦5 の範囲で h=0.5 とし、実際にオイラー法とルンゲ･クッタ法を用いて解け．

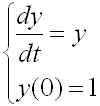
オイラー法を用いた結果と、同じ問にルンゲ･クッタ法を用いた結果が、微分解 y(t) = exp(t) とどの程度あっているか、gunuplot を用いて確認せよ．

結果は大体次のようになります．h=0.5とかなり粗く時間刻み幅をとっているにも関わらず、ルンゲ･クッタ法は良く微分解を近似できていることが わかります．それに比べてオイラー法は微分解から大きく離れてしまっています．これではオイラー法の結果は正しい計算とは言えないでしょう (もちろん h をもっと小くすれば、オイラー法でもよい近似を与えます.)．

 

 

 

 

　

ここで紹介したものは4次のルンゲ・クッタ法と呼ばれるもので，４次の精度をもっています．
つまり，y(t)=Y(t)として，
ルンゲクッタ法で時間刻み幅hだけ計算したものをY(t+h)とすると，
微分方程式の解y(t+h)をテイラー展開したものと，このY(t+h)はhの４次の項までは一致するということを意味しています．
オイラー法は，hについて１次項までは一致しているので解の精度は1次です．

ルンゲ・クッタ法とは，そもそもなにをやっているのでしょうか？
このルンゲ・クッタ法の仕組みを細かく計算して本当に４次の精度になるか確認したい人は是非やってみてください。
(ニューメリカルレシピ in Cなどが参考になると思います）
２次の精度のルンゲ・クッタ法ともいうべき方法は，中点法などが知られています．

様々な機械の「振動」が、このような方程式を応用しながら解析されています.

課題2

次の微分方程式

dy/dt = v

dv/dt = -y

を

y(0)=1, v(0) = 0，時間の刻み幅h=0.2

としてルンゲクッタ法でとき，(y(t), v(t))の軌道をgnuplotで描画せよ．

このとき，同じくh=0.2のもとオイラー法で計算した結果と比較すること．

参考までに，原点を中心とした半径1の円と，h=0.2のもとオイラー法で計算した結果を下図に示す．

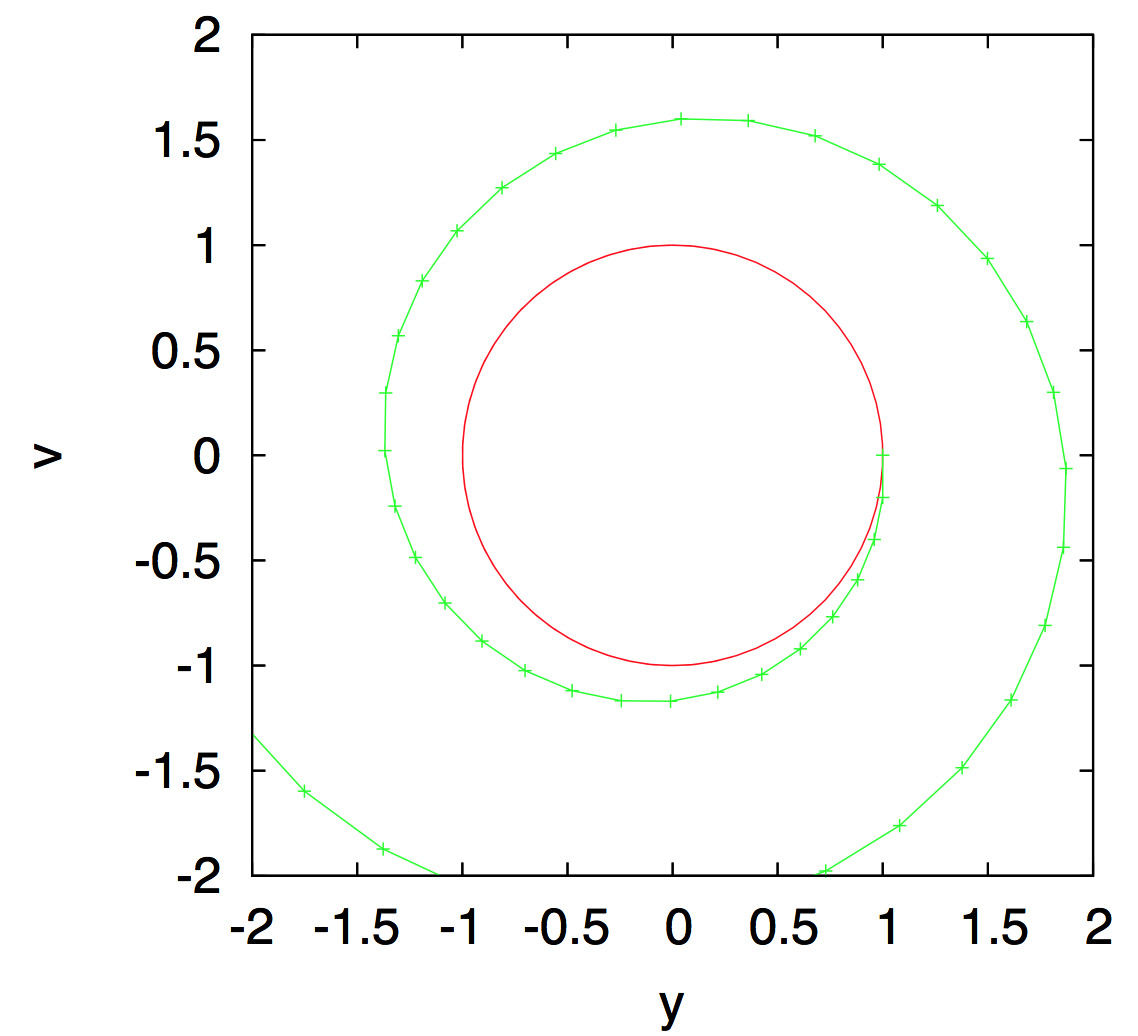
課題3

次の微分方程式

dy/dt = v

dv/dt = - v + y - y³

をルンゲクッタ法でとき，

初期値y(0),v(0)によって，最終的に落ち着く点（収束する点）が変わることを調べよ．

ただし，距離0.0001以内に(y(t),v(t))が存在すれば、(y_fix, v_fix)に収束しているとみなすことにする。

（ヒント：収束する先の点はyが正のもの，yが負のものの二点が見つかるはずである．）

応用問題

課題3で，

どのようなy(0),v(0)を選べば，yが正の点に収束するのか．

その初期値(y(0),v(0))の集合をAとして，

Aをyv平面上に図示するためには，どのようなプログラムをつくる必要があるか考えてみよ．

課題4

次の微分方程式

dy/dt = v

dv/dt = - y + A*cos(w*t)

をルンゲクッタ法で数値的に解いて、A = 0.1と固定して、w = 0.61, 0.95, 1.0, 1.05の場合の y(t) の時間変化を0≦t≦400の範囲で調べよ．

ただしy(0) = 1.0 , v(0) = 0.0 とする。(時間の刻み幅hは0.01となるようにせよ)

 

また課題３同様、y と v の関係（gnuplot で横軸を y, 縦軸を v として）も plot してみて下さい. 　

 

 

（w = 1.0の場合、系自身が持っている振動数と外力の振動数が完全に一致します。このとき、共振と呼ばれる現象がおこり、振幅がt→∞で発散することがあります。確認してみてください。）

課題5

次の微分方程式

dy/dt = v

dv/dt = - 0.3*v - y³ + B*cos(t)

を数値的に解いて、B = 0, 1, 6, 12 の場合の y の時間変化を調べてください．また課題３同様、y と v の関係（gnuplot で横軸を y, 縦軸を v として）も plot してみて下さい. これは、バネが大きく伸び縮みすると急激に硬くなるような場合の、強制振動系です.特に y, v の初期値が少し違う場合の. y の時間変化を比較してください. 課題３とどのような特徴の違いがあるでしょうか.

ハードディスクから原子炉まで、様々な機械の「振動」が、このような方程式を応用しながら解析されています.