計算数理A演習第10回 – Masashi Shiraishi Homepage

１次元拡散方程式の数値解法

１次元拡散方程式（１次元熱伝導方程式とも呼ばれる）の初期値境界値問題を数値的に解きます．
それは，次のようなものです．（記号など多少異なるかもしれません．）

問題１

(1) $\begin{equation*} \left\{ \begin{array}{lc} \frac{\partial u(x, t)}{\partial t} = D\frac{\partial^2u(x, t)}{\partial x^2} + f(x, t) & (0 < x < \ell, t> 0) \\ u(0, t) = a, u(\ell, t) = b & (t>0) \\ u(x, 0) = u_0(x) & (0<x<\ell) \\ u_0(0) = a, u_0(\ell) = b & \end{array} \right. \end{equation*}$

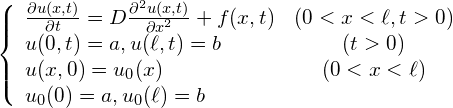
この問題の近似解を数値計算にて求めるのが今回の目標です．
まずは，上問題の特別な場合として次の問題を考えましょう．
なお，式中の D は拡散係数または熱伝導率とよばれます．

問題１．１

(2) $\begin{equation*} \left\{ \begin{array}{lc} \frac{\partial u(x, t)}{\partial t} = D\frac{\partial^2u(x, t)}{\partial x^2} & (0 < x < 1, t> 0) \\ u(0, t) = 0, u(1, t) = 0 & (t>0) \\ u(x, 0) = 2x(1-x) & (0\le x \le 1) \end{array} \right. \end{equation*}$

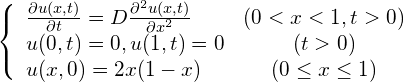
この方程式は拡散方程式、もしくは熱伝導方程式と呼ばれます。
拡散とは物が散らばっていく様子（例：コップにインクを垂らすと、時間とともに広がって最後には一様になる）であり、熱伝導とは熱が伝わる様子（例：スプーンを熱湯に浸けていると徐々に熱が伝わって持っている部分まで熱くなる）であります。
これらの現象を表現しているのが上式なのです。
「物の散らばり」と「熱の伝わり」という異なる現象が同じ方程式で表されるという面白さがあります。
熱伝導方程式と見ると $u(x,t)$ は時刻 $t$ での温度分布、拡散方程式とすると $u(x,t)$ は粒子の密度分布に対応します。

ここでは, $x = 0$ と $x = L$ でいつも $u = 0$ となるディリクレ条件を境界に課しています。
温度の分布の言葉でいうと、両端を氷か何かでつねに冷やしている状況を考えていることになります。
つまり、熱が両端からどんどんと奪われているわけです。

さて，計算機で扱えるよう離散化し，数値的に近似解を求めます。
ここでは，問題１．１を例にすすめますが，問題１に対しても同様に離散化できます．

分割方法は以下の２種類が考えられますが，

ここでは（講義の説明に従い）時間方向の離散化は(1)を，空間方向の離散化は(2)を採用します。
（これまでの演習で常微分方程式の数値解法を扱ったが，そこでは時間方向の離散化として(1)を採用してきた）

$h, \tau$ はそれぞれ $x, t$ に関する格子点の間隔とすると、 $[0, L]$ 区間を $N$ 等分するとし，
上記離散化方法に従い， $h=L/N, \tau>0$ とし， $x_j = (j - 1/2)h, t_k = k\tau$ おくことができ、

$U^k_j \approx u(x_j, t_k), \ \ (j=1, \cdots, N, k= 0, 1, \cdots)$

と書くことができます。
今回は、考える区間が $[0,1]$ であるので、 $L=1$ です。
$h, \tau$ はそれぞれ， $h = 1/N, x_j = (j - 1/2)h,　t_k = k\tau$ となります。

差分方程式

$\frac{\partial u(x, t)}{\partial t} = D\frac{\partial^2u(x, t)}{\partial x^2}$

は次の差分方程式で近似されます．

$\frac{1}{\tau} (U_j^{k+1} - U_j^k) = \frac{D}{h^2}(U_{j-1}^k - 2U_j^k + U_{j+1}^k), \ \ (j=1, \cdots, N, k= 0, 1, \cdots)$

これを書き換えれば，

$U_j^{k+1} = \alpha U_{j-1}^k + (1 - 2\alpha) U_j^k + \alpha U_{j+1}^k, \ \ (j=1, \cdots, N, k= 0, 1, \cdots)$

が得られます。ただし， $\alpha = D\tau / h^2$ としました．
この式は見てのとおり，時刻 $t^k$ での $u$ から次の時刻 $t^{k+1}$ での $u$ の値が計算できる形をしています。

ようは，これをプログラムにすればよいわけです。
後は，初期条件と境界条件（今回はディレクリ条件）ですが，それらはそれぞれ次のようになります．

$U_j^0 = 2x_j(1-x_j)$

$U_0^k = -U_1^k, U_{N+1}^k = -U_N^k, \ \ (k=0, 1, 2, \cdots)$

これで，準備はできました．

次に拡散方程式を計算機にて解くためのアルゴリズムを考えましょう。
解を求める時刻の上限を $T$ とし，適当な自然数 $M$ を定めて， $\tau = T/M$ とします。
問題１．１を解くアルゴリズムは次のようになります（ただし， $D=1.0$ とした）。

アルゴリズム

ライブラリのインポート

（１） 変数と初期パラメータを設定

T（時間上限）, M（時間刻み数）, L（空間幅）, N（空間刻み数）, D（拡散係数） を設定する
h = L/N, τ = T/M, α = Dτ/h2　(プログラム中では, τは「tau」, αは「alpha」等とする.)
x[N+2], u[N+2], new_u[N+2]（偏微分方程式の変数を配列として準備する。） 
　
（２） 初期値設定
j := 1,....,N の順に
    x[j] = (j - 0.5)*h
    u[j] = 2*x[j]*(1-x[j])
を繰り返す
u[0] = -u[1], u[N+1] = -u[N] 　　（境界条件）

描画する準備
figとaxをつくり，最初の状態のuを描画する。

（３）時間発展を計算
k := 0,1,.....,M-1 の順に
    （３.1）計算
    j := 1,2,....,N の順に
        new_u[j] = αu[j-1] + (1 - 2α)u[j] + αu[j+1]
    を繰り返す
    j := 1,2,....,N の順に
        u[j] = new_u[j]
    を繰り返す
    u[0] = -u[1], u[N+1] = -u[N] 　　（境界条件）
    （３.2）(x1, u[1]) ～ (xN, u[N]) を画面に表示
    (ただし x[0], u[0], x[N+1], u[N+1] は境界処理用なので表示しない)
    更新されたuを描画
    plt.pause関数で絵を更新
を繰り返す

このアルゴリズムを実現するプログラムを作成せよというのが当面の課題となります．

課題１

上のアルゴリズムに従ってプログラムを完成させよ。
ただし， $T=0.5, M=5000, L=1.0, N=50, D=1.0$ 程度，
初期条件は $u(x,0) = 2x(1-x)$ ，境界条件はディリクレ条件とする。

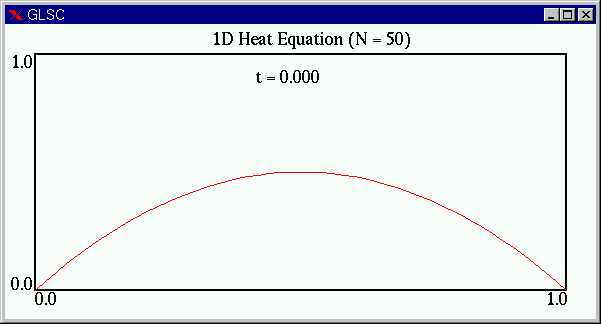
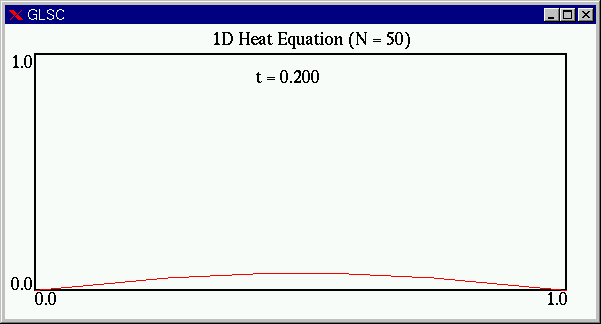
実際の計算部分を正しくプログラムにすることができれば，次のようなアニメーションを見ることができます．
両端から熱（物質）が奪われ，全体の温度（密度）が下がることがわかります．