今日の演習
- グローバル変数とローカル変数
- 常微分方程式の数値解法ーオイラー法
- 差分商
- オイラー法のアルゴリズム
- 簡単な常微分方程式とその数値解のグラフ化
- レポート課題(2019年5月8日水)
- 自由課題
- 1階常微分方程式の数値解法
- オイラー法による2階常微分方程式の解法
グローバル変数とローカル変数
これまでに特に断りなく変数を初期化して利用してきました。関数もいくつかの例題で学びましたが,関数をより効率的に利用するために必要なグローバル変数とローカル変数についての基礎的な内容を学びます。
Pythonでは段落(インデント)をつけることが階層を決める重要な要素と説明しましたが,一番左よりな状態で変数を初期化すればグローバル変数としてどこでも変数として利用できます。
そして,関数内で初期化したものは関数の中だけでしか利用できず,関数の中で変更した変数は関数の外ではreturnで結果を受け取らなければ変数に影響は与えません。このような部分的にしか利用できない変数をローカル変数と言います。
# global変数の宣言
global_i = 0
global_j = 0
def func1():
# グローバル変数はどこでも参照できる
print(f"global_i = {global_i}")
def plus_some(number):
# そのままで「書き換え」となる代入ができないので以下の宣言が必要
global global_i
global_i += 100; # global_i = globa_i + 100 の意味
number += 10
global_j = 100
local_i = 0
func1()
# エラーになる
#print(number)
plus_some(local_i)
print(f"global_i = {global_i}, global_j = {global_j}, local_i={local_i}")
plus_some(local_i)
print(f"global_i = {global_i}, global_j = {global_j}, local_i={local_i}")
global_i += 100
func1()
サンプルコードで言えば,local_iの値をnumberに代入してそこに10を足していますが、足されたのはあくまでもnumberであり,グローバル変数であるlocal_iではありません。
また,これはpythonの仕様でグローバル変数はどこでも数値や文字列を利用することは出来ます(func1の呼び出しで数値が表示される)が,plus_some関数のように中で100を加えて数値を変更仕様とするとそのままではエラーが出てくるため,globalと変数の前に書いて宣言をすることで利用する変数がグローバル変数にあるglobal_iであることが認識されます。
もう一つのglobal_jもplus_some関数で利用されていますが,ここでは代入だけを行うと関数の外でprintしても数値に何の変化も生じていません。これはpythonではローカルに初期化された変数が優先するためで,同じ名前でもグローバル変数は無視されるので注意してください。
また最後にglobal_iに変更を加えて,func1関数を呼び出すと数値がまた変化しているのがわかります。このようにグローバル変数を用いるとその関数がどこで使われているかにより,出てくる値が変わるため気をつけなければいけません。
関数を利用するときは,変数を変化させたいときはreturnで変化した結果を返して=で上書きしたい変数に代入する様にしてください。また,グローバル変数は数値計算において変更がないパラメータなどに限定して利用するようにしてください。
global_i = 0 global_i = 100, global_j = 0, local_i=0 global_i = 200, global_j = 0, local_i=0 global_i = 300
常微分方程式の数値解法(オイラー法)
今回は次のような常微分方程式の初期値問題を、オイラー法と呼ばれる方法を用いて数値的に解いて結果をグラフにしてもらいます。
オイラー法は計算数学演習で扱っていますが, おさらいをしておきます。 次の問題を考えます。
(1) 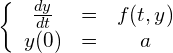
求めたいのは、![]() の範囲の
の範囲の![]() であり、関数
であり、関数![]() および定数
および定数![]() は与えられているとします。
は与えられているとします。
また、![]() の値は
の値は![]() が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
コンピューターでは数値を離散的に(とびとびに)しか扱うことができません。
そこで、(1)式をコンピューターで扱えるようにする必要があります。
(1)式をコンピュータで解く方法には色々とありますが、今回は代表的なものの一つであるオイラー法を用います。
その前に、準備として差分商について説明します。
差分商
![]() を
を![]() の関数としたとき、
の関数としたとき、![]() の
の![]() における微分係数は
における微分係数は
(2) ![]()
で定義されます。ここで、定義中の極限操作を取り払い、![]() を有限にとどめた
を有限にとどめた
(3) ![]()
を考えると、![]() を十分小さな正の実数ととれば、(3)式は(2)式の近似となっていると考えられます。
を十分小さな正の実数ととれば、(3)式は(2)式の近似となっていると考えられます。
この![]() のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、(3)式の右辺のような量を差分商といいます。
のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、(3)式の右辺のような量を差分商といいます。
いまの場合は1階微分係数を近似する1階差分商です。
では、このような差分商を用いて(1)式を離散化してみましょう。
まず、(1)式の第一式の微分係数を上記の差分商で置き換えてみます。
(4) ![]()
ただし、![]() は正の数とします。
は正の数とします。
(4)式と(1)式の第一式は異なる方程式なので、(1)式の第一式の解 y(t) は一般に(4)式を満たしません。
そこで、混乱を防ぐために(4)式の![]() を
を![]() と書き換えましょう。
と書き換えましょう。
(5) ![]()
(??)式のように差分を含む方程式を差分方程式といいます。
次に、(1)式の![]() を
を![]() に置き換えた初期条件
に置き換えた初期条件
(6) ![]()
(7) ![]()
と変形できるので、![]() を代入すると、
を代入すると、
(8) ![]()
となり、![]() から直ちに
から直ちに![]() が求まります。同様にして(7)式を繰り返し用いると、
が求まります。同様にして(7)式を繰り返し用いると、
(9) 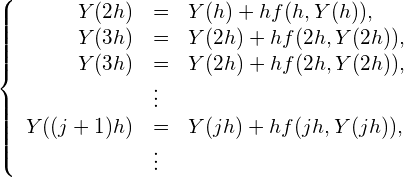
というように、![]() とすると
とすると![]() を
を![]() から計算できることがわかります。
から計算できることがわかります。
![]() をいったん決めると、
をいったん決めると、![]() 以外の時刻の
以外の時刻の![]() の値は(7)式からは求めることができません。
の値は(7)式からは求めることができません。
このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります。
そのようなとびとびの時刻を格子点と呼びます。![]() は格子点でのみ意味があるので、そのことを明示するために
は格子点でのみ意味があるので、そのことを明示するために![]() を
を![]() と書き換え、
と書き換え、![]() とすると、(5)式と初期条件は、
とすると、(5)式と初期条件は、
(10) 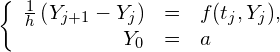
となり、結局(1)式の常微分方程式の初期値問題が、![]() に関する漸化式の問題(10)式に置き換えられました。この方法をオイラー法と呼びます。見やすいように(10)を書き直すと
に関する漸化式の問題(10)式に置き換えられました。この方法をオイラー法と呼びます。見やすいように(10)を書き直すと
(11) 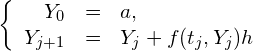
となります。
オイラー法のアルゴリズム
解を求める時刻の上限を![]() とし、適当な自然数
とし、適当な自然数![]() を定めて
を定めて![]() とする。
とする。
T, h, a 及び 関数 f は実数型(float)
N, j は整数型(int)
Y[N+1], t[N+1] は実数型配列(float)
T, N, aを設定
配列Y[N+1], t[N+1]を用意する
h = T/N (TおよびN双方が整数型でないか注意)
Y[0] = a (初期条件の設定)
t[0] = 0
j = 0, 1, 2, ..., N-1の順に(for文)
t[j+1] = (j+1) * h
Y[j+1] = Y[j] + h * f(t[j], Y[j])
以上をj=N-1まで繰り返す。
matplotlibを使ってグラフを描く
f(t,Y) は関数(上で復習してます)として定義するとよい.
簡単な常微分方程式とその数値解のグラフ化
さて,実際にオイラー法をつかって常微分方程式を解いてみましょう.
今回も、計算数理Aの講義に出てきた次の常微分方程式を用いて演習を進めます。(ただし![]() を
を![]() と書き換えた.上記アルゴリズム等の分割数
と書き換えた.上記アルゴリズム等の分割数![]() とまぎらわしいので.)
とまぎらわしいので.)
(P) 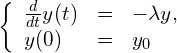
前回は,この微分方程式を解析的に解いて得られた解をグラフ化してもらいました。今回は(P)式をオイラー法を用いて数値計算で解いて,得られた数値解をグラフ化してもらいます.
課題1
(P)をオイラー法で解き,得られた数値解をグラフとして表示するプログラムを作成せよ.ただし,
![]()
とする。例えば次のようになる。
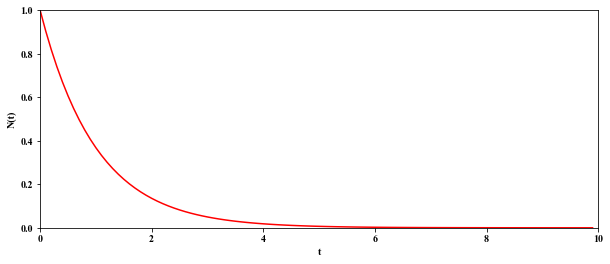
(この例では、![]() を100等分している。つまり時間刻み幅を h と書くことにすると、 h = 10.0/100 = 0.1 である。)
を100等分している。つまり時間刻み幅を h と書くことにすると、 h = 10.0/100 = 0.1 である。)
(縦軸がN(t)となっているがy(t)と読み替えてください.)
先週,解析的に求めた解をグラフとして表示したものは以下であるが,殆ど違いがない事に注意.
(課題3でみるが,微妙に異なっている)
課題2
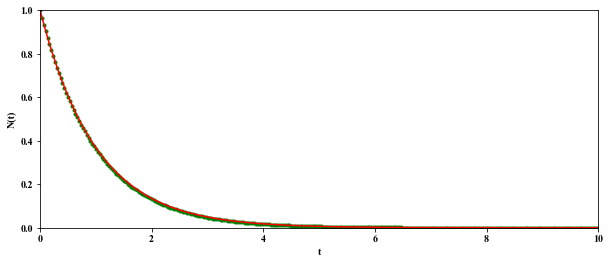
前回解析的に求めた解(S)とオイラー法で求めた数値解を重ねて描くプログラムを作成せよ.
例えば,次のようになる.
この例では,解(S)を緑色で描き,数値解を赤色で描いている.
(この例では、0≦t≦10 を 100等分している)
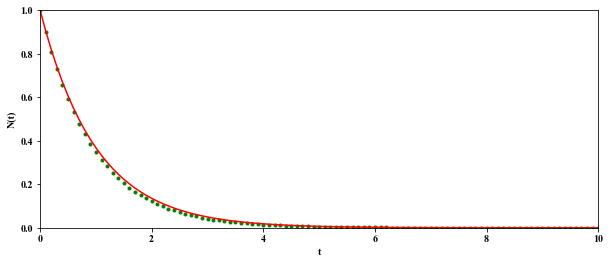
刻み幅を小さくすると両者の差は縮まる.(次の例では、0≦t≦10 を 300等分している)
課題3
次の常微分方程式の初期値問題をオイラー法で解き,t と y の関係をグラフ化せよ.
(1) dy/dt = -y + sin(t), y(0) = 1 (時刻 0≦ t ≦20 の範囲を20000等分割、100ステップ毎に値を表示)
(2) dy/dt = y(5-y), y(0) = 1 (時刻 0≦ t ≦20 の範囲を20000等分割、50ステップ毎に値を表示)
(3) dy/dt = y – 2y3, y(0) = 0.1 もしくは y(0) = -0.1 (時刻 0≦ t ≦20 の範囲を20000等分割、100ステップ毎に値を表示)
レポート課題
課題2で作成したプログラムを少し変更して,
「λの値の入力を促し,そのλの値における解析解とオイラー法で求めた数値解を重ねて表示する」
プログラムをrep20190424.pyもしくは(.ipynb)という名前で作成し,Bb9から提出して下さい.
初期値,x,yの表示範囲は課題3と同じでかまいません.
0≦t≦10 を 100等分とすること.数字や軸の名前が描いてあるかどうかも評価のポイントです.関数を作ってmain関数をシンプルに(読み易く)記述しているものは高く評価します.
インデント(時下げ),コメントは必ず行うこと.
また,プログラムの最初の方にコメントとして学生番号と氏名は(最低限)必ず記述すること.
(# bxxxxxx 氏名)
提出期限2019年5月8日(水)12時00分
自由課題(上記の課題が終わった人へ)
一次元セルオートマトンについて調べて描いてみてください.
ただし,各xセル(値は0か1)は自分の値と両隣の値をもとに,次の時刻の自分の値を決定する物とします.
(セルの数は自由に設定してください)
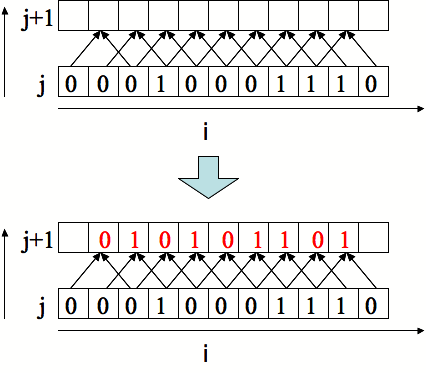
例としてRule90と呼ばれるもの以下に示します.
(iがセルの番号で,jが時刻を表すと思ってください)
また時間発展のルールを変更したときに,どのようなことがおこるのか試してみてください.
(この枠組みだと時間発展のルールは256通りです.)

1階常微分方程式の数値解法
前回,簡単な1階常微分方程式をオイラー法にて解いてもらいました.
いくつか講義で出てきた問題をあげておきます.
オイラー法で解いてみて,解をグラフとして表示してみてください.
初期値やパラメータを適当にきめて,いくつかシミュレーションしてみてください.
(12) 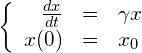
(13) 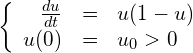
オイラー法による2階常微分方程式解法
2階常微分方程式もオイラー法を用いて解くことができます。
次の問題を考えて行きましょう。
(14) 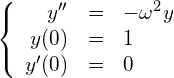
講義の説明の通り(下の枠中)、これは単振動を記述する2階の常微分方程式です。
ただし簡単の為、時間
バネ定数
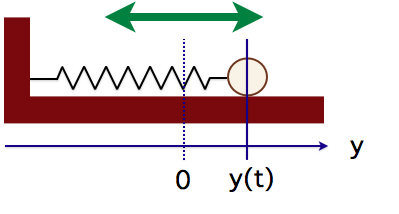
このおもりを少しだけ右に引っ張ってから手を放す。
おもりの中心の時刻![]() におけるつり合いの位置からのずれを
におけるつり合いの位置からのずれを![]() とすると,
とすると,![]() が満たす微分方程式は
が満たす微分方程式は
(15) ![]()
ただし、
(16) ![]()
とした。
2階の常微分方程式は次のように連立の1階の常微分方程式に帰着できます。![]() とおくと、式(14)は、
とおくと、式(14)は、
(17) 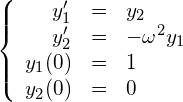
となります。
この形になれば、前回紹介したオイラー法を用いて解を求めることができます。
アルゴリズムは次のようになります。
但し、
また、変数は
また、
オイラー法のアルゴリズム
解を求める時刻の上限を T とし、適当な自然数 N を定めて h=T/N とする。
T, h, a1, a2, y1, y2, y1_new, y2_new, t 及び 関数 f1, f2 は実数型
N, j は整数型
T,N,h を定める
配列y1[N+1], y2[N+1], t[N+1]を用意する
f1(t,y1,y2), f2(t,y1,y2) を関数として定義
y1[0] = a1, y2[0] = a2, t[0] = 0
j = 0,1,2,....,N-1の順に
t[j+1] = (j+1)*h
y1[j+1] = y1[j] + h*f1(t[j], y1[j], y2[j])
y2[j+1] = y2[j] + h*f2(t[j], y1[j], y2[j])
を繰り返す
matplotlibでグラフを描画
課題4
式(14)を解析的に解け。
課題5
![]() として式(17) をオイラー法で解き、グラフを描け。グラフは横軸が
として式(17) をオイラー法で解き、グラフを描け。グラフは横軸が![]() であり、縦軸を
であり、縦軸を![]() とせよ。
とせよ。
また、時間刻み幅![]() を変えたときに結果がどのようにかわるか観察せよ。
を変えたときに結果がどのようにかわるか観察せよ。
0≦t≦20の範囲において、h=0.0001,0.001, 0.01, 0.1それぞれの場合について、解析解とどの程度あっているか各自調べよ。
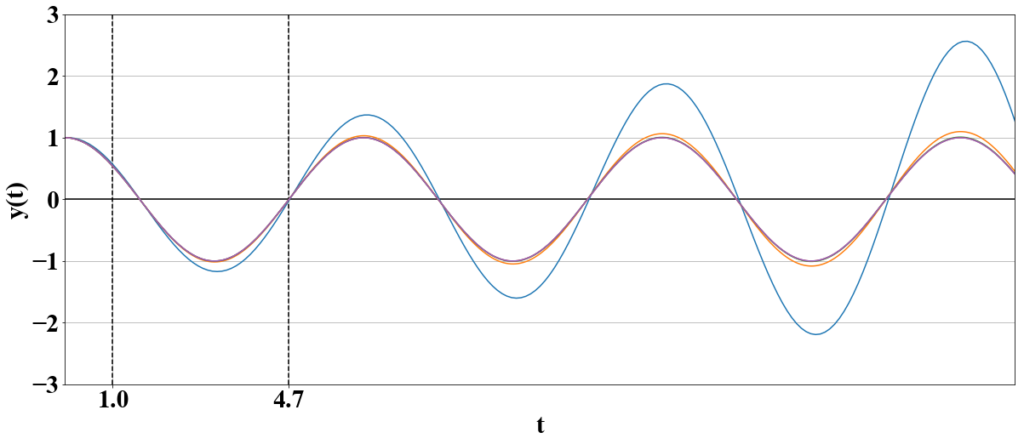
色々な h に対する計算結果は次のようになる(青はh=0.1、オレンジはh=0.01、緑はh=0.001、赤はh=0.0001のときの結果。紫は解析解のグラフ)。
この結果から、h は十分小さい値でないとまずいことがよく分かる。
オ イラー法では h を十分小さくとらないと本当の解をうまく近似できません。h を小さく取るということは、計算時間が多くかかることを意味します。そこでより高精度で大きな h でもうまく解を近似できるような解法が求められます。そのような要求に応える解法としては、ルンゲ・クッタ法があります。
課題6
課題5のプログラムを用いて、
(18) ![]()
を計算せよ。
結果は、横軸を
この
課題7
先程単振動を考察しましたが, 実際のバネではバネの復元力以外におもりの速度![]() に比例する抵抗が働く。
に比例する抵抗が働く。
その抵抗を考慮すると、式(14)ではなく次の式になる。(![]() の項が新たに加わった。)
の項が新たに加わった。)
(19) 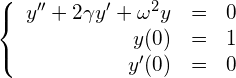
ここで
式(19)の問題を連立1階常微分方程式に変換し、オイラー法を用いて解き、下のように「左端から線の繋がった赤い質点が振動する」動画を作成してください。
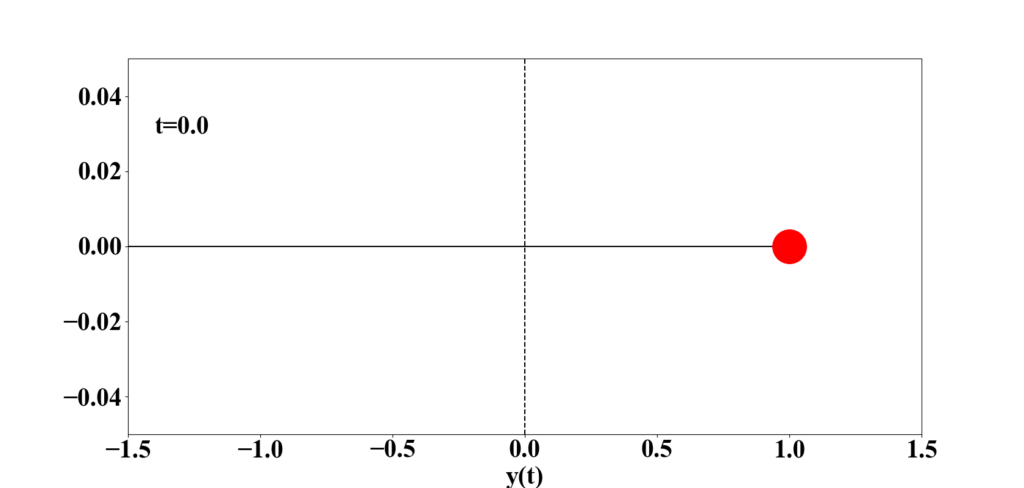
ただし、![]() とし、時間の刻み幅
とし、時間の刻み幅![]() は、0.01とします。
は、0.01とします。
ます。また、左上の”t= ..”は現在の![]() を表示している。
を表示している。
デモプログラムでは、時間の刻み幅は![]() として、
として、![]() まで計算しています。
まで計算しています。
また、提出するプログラムでは、アニメーションの描画を![]() が
が![]() 動く毎におこなうようにしてください。(ヒント1: “%”をつかったif文)
動く毎におこなうようにしてください。(ヒント1: “%”をつかったif文)
これは、無駄にプログラムの実行時間が長くなるのを防ぐためです。
以下、アドバイス等:
“t=”の部分のアニメーションのさせ方:
他の点や棒の表記と同様にオブジェクトとしてテキストを作り,それをset_text関数を使って更新していきます。簡単な例は以下のようになります。
注意点はax.plotではline, のようにカンマをつけていましたが,textにはいりませんのでよくよく注意してください。
%matplotlib tk
import numpy
import matplotlib.pyplot as plt
T = 100
h = 0.01
fig = plt.figure()
ax = fig.add_subplot(111)
t = 0.0
txt = ax.text(0.3, 0.5, f"t={t:.2f}", transform=ax.transAxes)
for i in range(T):
t = i*h
txt.set_text(f"t={t:.2f}")
plt.pause(0.01)
課題8
下図のような重力下で棒の長さ![]() が一定の振り子運動について、振り子の角度(ラジアン)を
が一定の振り子運動について、振り子の角度(ラジアン)を![]() とすると
とすると![]() は
は
(20) ![]()
という運動方程式を満たす(![]() は重力加速度、摩擦は無視しています)。
は重力加速度、摩擦は無視しています)。![]() として、この方程式を適当な初期条件、
として、この方程式を適当な初期条件、![]() でシミュレーションし振り子の動画を作成せよ。
でシミュレーションし振り子の動画を作成せよ。
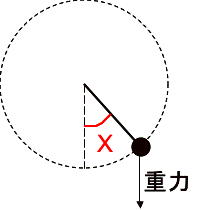
今回の課題は、オイラー法では十分に小さい![]() を用いないと計算結果がすぐにずれてしまいますが, 練習としてやってみてください.
を用いないと計算結果がすぐにずれてしまいますが, 練習としてやってみてください.
次回, オイラー法より計算精度の高いルンゲ・クッタ法を紹介しますが, そのときに比較してみてください.
課題9
課題7の振り子が2つ相互作用する場合を考える.
例えば, 2つの振り子の角度を![]() とすると、
とすると、![]() が
が
(21) 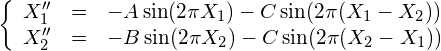
という運動方程式を満たすとする。
この方程式を適当な ![]() と初期条件、
と初期条件、![]() でシミュレーションし、振り子のアニメーションを作成せよ.
でシミュレーションし、振り子のアニメーションを作成せよ.
また振り子の数をもっと多くした場合も考察せよ.