私たちの研究室が主体となって行っている（きた）研究　

１　グラフェンの量子輸送 ２　トポロジカル絶縁体
３　非平衡超伝導現象　　　 ４　微小トンネル接合の物理 ５　幾何学的共鳴磁気抵抗

 

1  グラフェンの量子輸送

　   以下はグラフェン（サンプル）の作製技術

 

 

NEW: 　グラフェン中の電子の弾道伝導に電子構造の異方性が表れることを発見

Takushi Oka, Shingo Tajima, Ryoya Ebisuoka1, Taiki Hirahara1, Kenji Watanabe, Takashi Taniguchi2, and Ryuta Yagi1*,Ballistic transport experiment detects Fermi surface anisotropy of graphene, Phys. Rev. B 99, 035440 (2019). DOI: 10.1103/PhysRevB.99.035440.

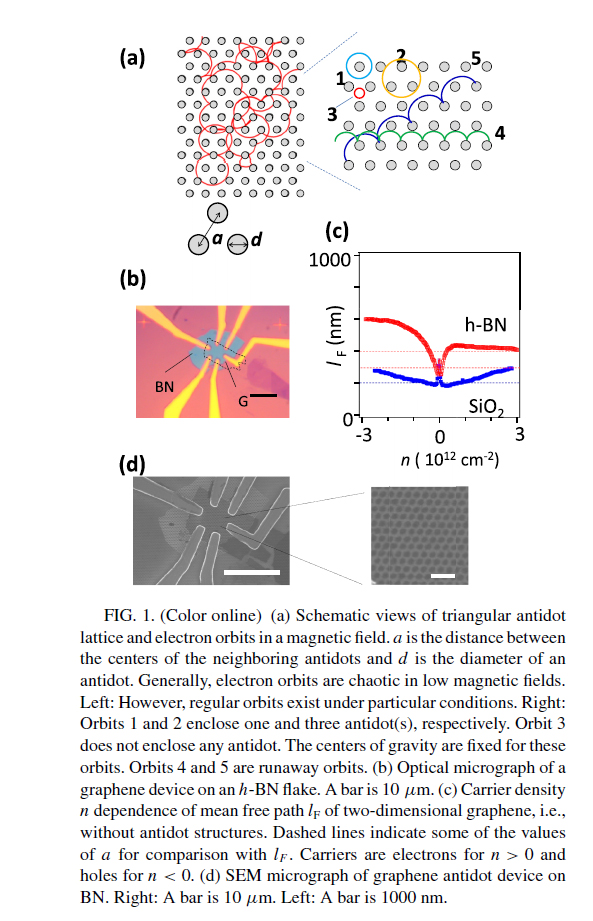
単層グラフェンのフェルミ面の形はほとんど真円に近いが、二層グラフェンのフェルミ面の形は、実は「おにぎり型」にゆがんだ円になっていることが予想されてきた。こうした、電子系の異方性を、電子の空間運動を調べることで明らかにした。フェルミ面の形状が円からゆがむと、磁場を加えた時に現れる電子のサイクロトロン軌道の形が円からゆがんだ円になる。こうした振る舞いを、導体中の電子の弾道伝導として、規則的に穴が開いたアンチドット格子を用いて、磁場中電気伝導によって検出することに成功した。

 

力学的に剥離したグラフェンでは、直線的な劈開線が見らえる。これは、ジグザグエッジ方向かアームチェアエッジ方向になっている。この劈開線を基準に微細加工によって穴の格子の軸の方位が異なる「グラフェンアンチドット素子」を作製。（下図）

 

 

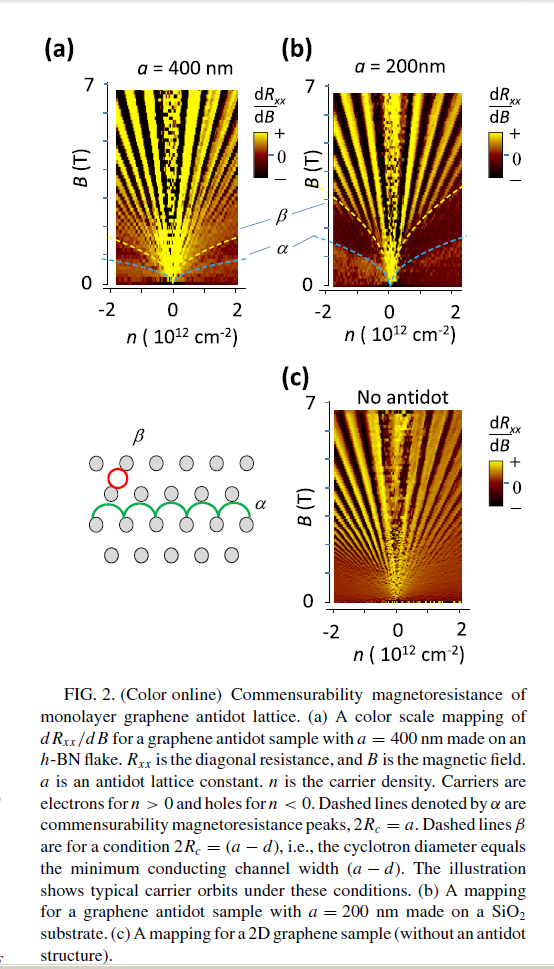
低温磁場中で、抵抗を測定。フェルミ面がおにぎり型にひずんでいる二層グラフェンでは、明らかな磁気抵抗のアンチドット格子方位依存性がみられた（下図(a)　振動を除いた部分の磁気抵抗の振る舞いに注目。）。しかし、フェルミ面の形が真円に近い単層グラフェンでは、アンチドット格子の方位に対する依存性がみられない。

 

磁気抵抗シミュレーション

以上のような実験で観測された振る舞いは、磁気抵抗数値シミュレーションによって説明される。フェルミ面の形の異なる以下のモデル化されたフェルミ面においてのシミュレーションでは、ちょうど、フェルミ面の形が２層グラフェンに近い場合には、実験を説明できることがわかりました。単層グラフェンにおいても、異方性が小さい（ほとんど見られない）ことがわかりました。　この、電子の磁場中実軌道の形をアンチドットという障害物で検出する方法は、二次元物質の電子構造を研究する新しい方法として期待できます。

 

NEW: グラフェンの電子構造　　原子層はいかにバルクに至るか？　

Ryuta Yagi, Taiki Hirahara, Ryoya Ebisuoka, Tomoaki Nakasuga, Shingo Tajima, Kenji Watanabe, and Takashi Taniguchi , Low-energy band structure and even-odd layer number effect in AB-stacked multilayer graphene, Sci. Rep. 8 13018 (2018). DOI:10.1038/s41598-018-31291-y

グラフェンは炭素原子の一枚膜です。これが２枚３枚と積み重なると、実は１枚の時とは違う性質が表れてきます。これは、ちょど、原子が集まって分子になり、あるいは結晶を作って金属や絶縁体などのいろいろな性質が出てくることと似ています。グラフェンが集まってどのようにグラファイトになっていくのかを研究すると、原子が集まっていろいろな性質が出てくる仕組みがわかるかもしれません。

ゲート電圧をかけて電子の数を制御し、磁場をかけた時に抵抗に振動が表れます。下の図では、それが筋として現れています。この筋のでかたは、層数が一層違っても全く違います。層数が増えるにしたがって複雑になり黒鉛に少しずつちかづいていっています。　それだけではありません。層数が奇数と偶数とで、グラフェンの質量ゼロのバンド（線形バンド）の有無が決まります。奇数層にはありますが、偶数層にはありません。

 

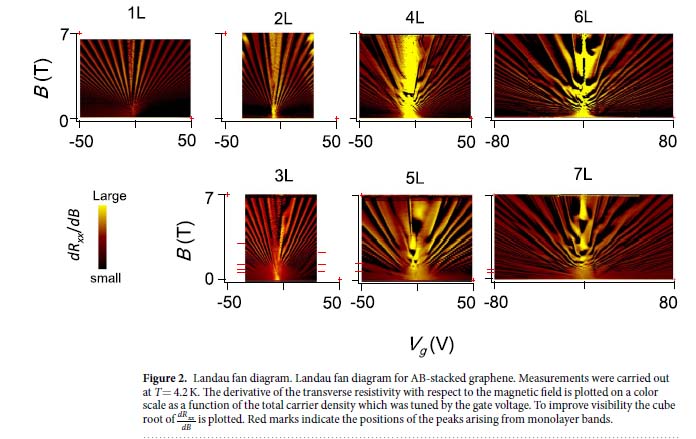
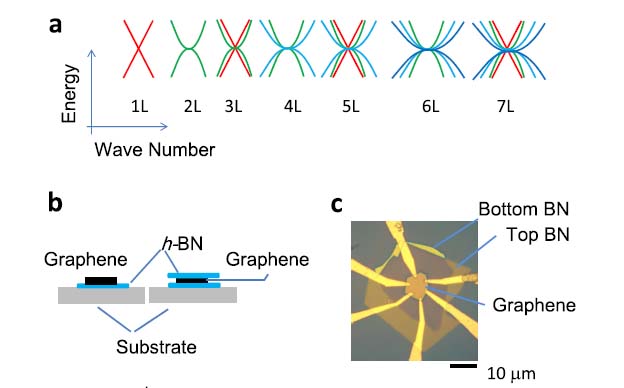
この実験は、研究室の多くの学生の力を結集して行ったものです。下の図は、グラフェンのバンド構造の概略と、この実験を行ったサンプルの構造を示しています。

　　　　　　　　　　　　　　　　

 

 

 

 

 

 

NEW: グラフェンのキャリア密度依存性に現れる固有抵抗ピーク構造　　バンド構造の現れ　

Taiki Hirahara, Ryoya Ebisuoka, Takushi Oka, Tomoaki Nakasuga, Shingo Tajima, Kenji Watanabe, Takashi Taniguchi and Ryuta Yagi, Multilayer graphene shows intrinsic resistance peaks in the carrier density dependence. Sci. Rep. 8 13992 (2018). DOI: 10.1038/s41598-018-32214-7.

ABスタック４層グラフェンにおいて、抵抗のゲート電圧依存性に複雑なピーク構造が表れる。トップゲートとバックゲートを持つサンプルで詳細に測定すると、抵抗の峰構造が表れる。

 

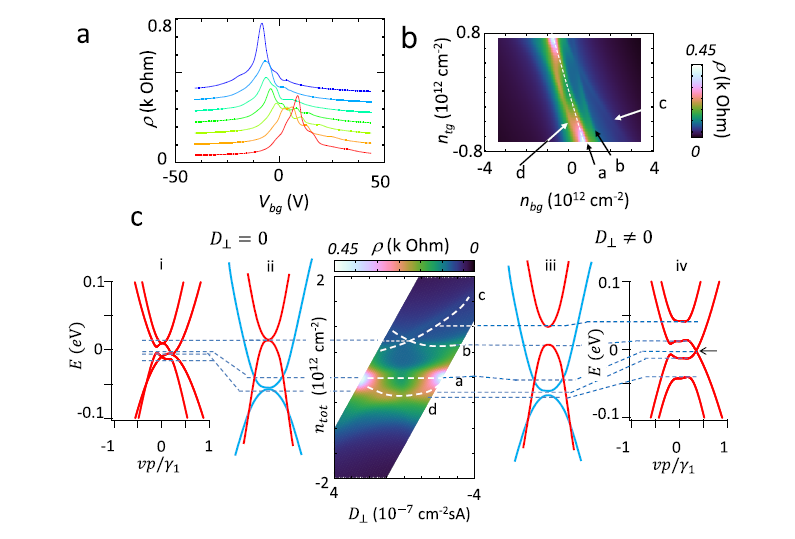
この峰構造は、バンド構造によって現れる。特に上に示した、点線でクロスしているｂとｃとは、軽いバンド質量をもつ二層バンドの底にできるゼロモードランダウ準位が分裂したものが表れている。（下の図を参照）下の図はランダウファンダイアグラム。

 

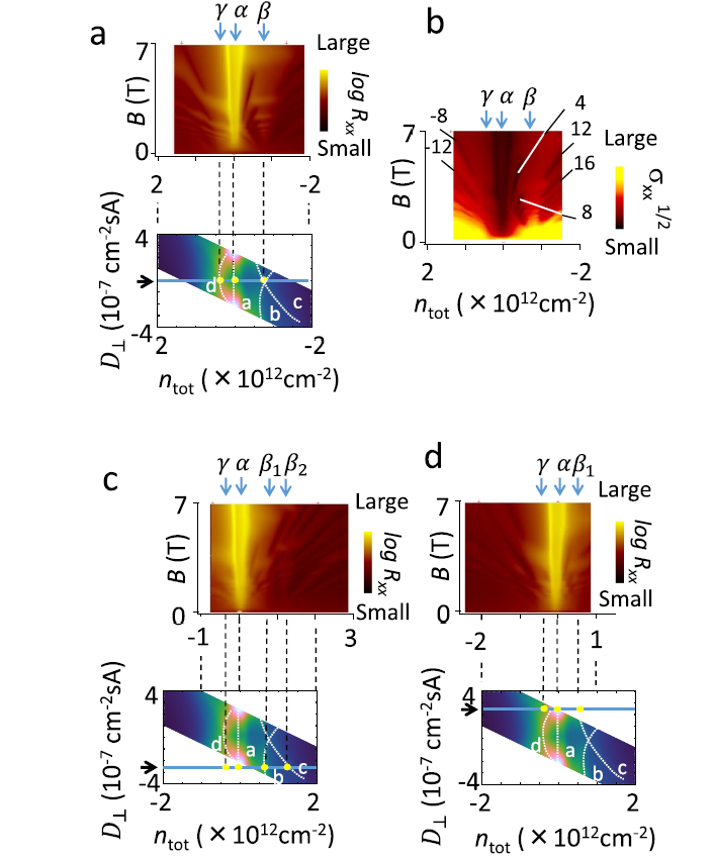
６層グラフェンにおいても、同種の現象がみられた。

 

Encapsulated High-Mobility Graphene 　

エンカプセルした超高移動度グラフェン

グラフェンは、他の有機半導体と比べて、きわめて大きな易動度を持つことが予想されています。しかし、実際に作られているデバイスの易動度は理論値をはるかに下まわっています。この原因は、グラフェンがふれている基板にあります。基板の中にある荷電不純物による散乱で易動度が下がります。写真に示されているのは、これを抜本的に回避する方法として注目されている、エンカプセルしたグラフェン素子です。荷電不純物が少なく、高品質で、原子平坦なh-BN（窒化ホウ素）でグラフェンを挟むことによって移動度が150,000cm2/Vs程度まで向上しました。平均自由行程（電子が散乱なく運動できる長さ）は数ミクロンに達します。この易動度は世界最先端レベルです。

Graphene has much higher mobility than any other organic semiconductors. However, the mobility can get much higher because substrates generally limit the mobility because of scattering due to charged impurity in the substrates. Here, we show graphene encapsulated by h-BN flakes that are high-quality and atomically flat. Electric mobility reached at about 150,000 cm2/Vs at low temperatures.

Optical micrograph of encapsulated graphene device. (c) Yagi lab.

 

 Ballistic Transport  in Graphene Antidot Lattices          

質量ゼロの電子の弾道的な伝導　　グラフェンアンチドット

R. Yagi et al.Phys. Rev. B 92, 195406 (2015).　　

  電子を粒子と見ます。周りに何も障害物がなく、磁場も電場もかかっていないときには、等速直進運動します。磁場がかかっていれば等速円運動をします。このようなことが実現できるのは、例えば電子が真空中におかれた場合です。このような運動をバリスティック運動といいます。　金属の中でも電子が動きますが、このようなことは実現できるのでしょうか。　一般には、難しいでしょう。金属の中には多数の散乱体があり、これに電子が衝突を繰り返して、電流が流れます。電子が散乱された後、次に散乱するまでの長さは、数オングストローム程度であるといわれています。

  さて、物質の中で、バリスティックな電子の運動は可能でしょうか？　答えはyes。うんと散乱体の少ない、純粋な物質を用意すればできます。たとえば、半導体ヘテロ接合二次元電子と呼ばれるものを使えば、電子は数ミクロン以上の長さにわたって散乱されないで動くことができます。

  新しく登場した物質グラフェンではどうでしょう？　グラフェンは、原理的に非常に散乱に強いという特性をもっているのですが、ふつうに作ったのでは表面がむき出しなので、様々な散乱を受けてしまいます。電子が散乱されないようにするには、原子平坦なhBN（窒化ホウ素）の上にグラフェンを乗せたり、さらにその上にhBNを乗せてエンカプセル化すれば良いことがわかってきました。

  この研究は、グラフェンの電子の弾道的な運動をアンチドット構造と呼ばれる構造で調べたものです。　実際に、散乱されずにバリスティックな伝導をすることがアンチドット構造で確認されました。これは、ディラック電子がバリスティック伝導という点で意義があります。　

   このような研究は、グラフェンを用いた高速デバイス、性能の良いディスプレー、携帯電話、コンピュータなどの電子機器の開発につながる可能性があります。

We have observed ballistic electron transport in antidot lattices of high-quality graphene that was made by transferring graphene on mechanically cleaved h-BN. We observed commensurability magnetoresistance peaks at the commensurability condition where cyclotron diameter matches lattice constant.

                  

   

              

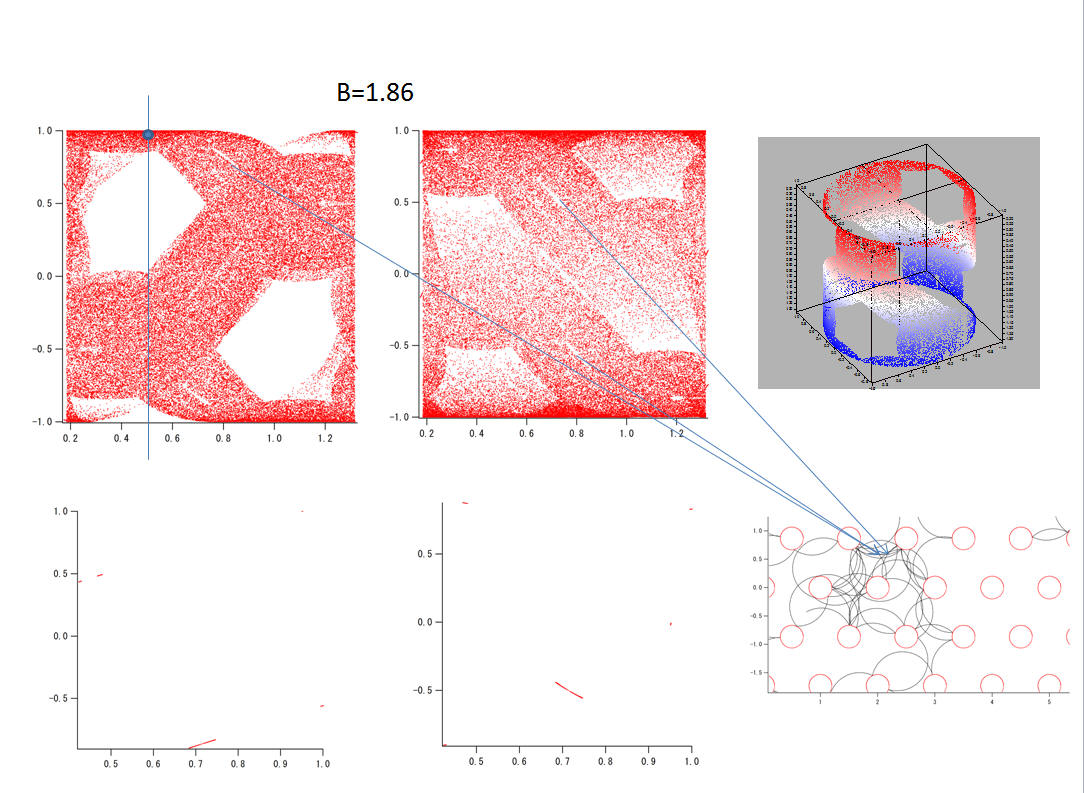
                 Poincare Section

Observation of Altshuler Aronov Spivak (AAS) Oscillation in Graphene  

グラフェンにおけるAAS振動の初観測

Yagi et al.  J. Phys. Soc Jpn. 81, 063707 (2012).

　少し前に、電子は、粒子であると書きましたが、量子力学的には、電子は波としての性質も持ちます。これをグラフェンで観測したのがこの研究です。

　Aharonv Bohm（AB）振動をご存知でしょうか。下図のようなリング状のサンプルでは、入射電子は二つに割れて、出るときにまた一緒になります。この時、電子が波の性質を持っているとすれば、干渉効果が起こります。それぞれの道筋で電子が獲得する位相に応じて、強めあい弱めあいの干渉が起こるため、電子波の透過確率が変化することで電気抵抗の振動が起こることが期待されます。実際、電子の獲得する位相は、ベクトルポテンシャルの影響を受けるため、リングを貫く磁束（磁場の大きさと、面積の積）に比例して大きくなり、電気抵抗は磁束h/eを周期として振動します。　これがAB振動です。AB振動を実際に観測するのは極めてたいへんです。試料中では散乱体がきわめてたくさんありますが、散乱される場所が違うpathに対応する電子波の寄与をすべて足し合わせなければならなく、そのような数は体系の大きさが大きくなればなるほど大きくなるため、干渉効果は平均化されて消えて行く傾向があります。

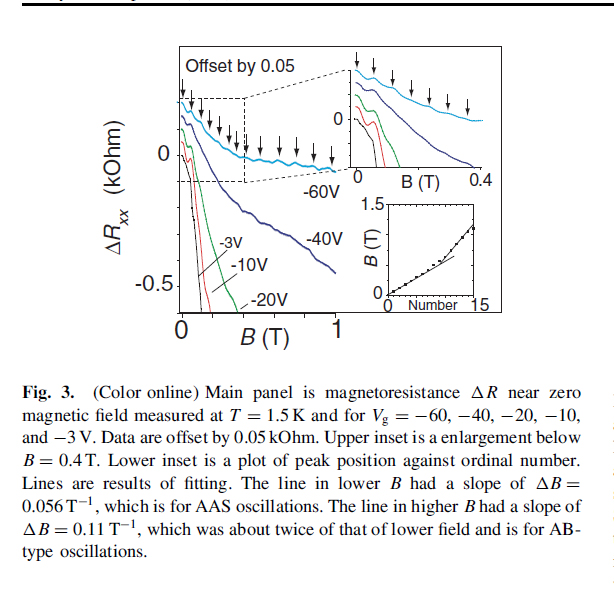
　AB振動と似て非なるもの、それがAAS振動です。AB振動を起こす電子経路があったとして、それと時間反転対称（つまり逆に動く）な電子経路の二つが干渉することで起こる振動と考えられます。電気抵抗が磁束h/2eを周期として振動します。AAS振動はAB振動よりもかなり強く残るものと考えられていて、実際に多数のリングからなる素子で観測できました。AAS振動は、二次元電子系の弱局在効果と深いつながりがあります。 

　本研究は、質量がゼロであるディラック電子で、初めてAAS振動を観測したことに意義があります。通常電子と同じように見えるのか違うように見えるのかは実験するまでわかりません。私たちは、AAS振動の位相が、通常のベリー位相の効果から期待去れるのとは反転されたものが観測されるのを見出しました。それは、グラフェンの中で頻繁にK点とK'点の間のバレー間散乱が起こっていること示しているとおもわれます。このような研究は、グラフェンの量子位相を用いた高速デバイスにつながる可能性があります。

AAS oscillation arises from quantum interference of coherent back scattering for a pair of  electrons with time reversal symmetry. This is the first observation in grahene system.

                             

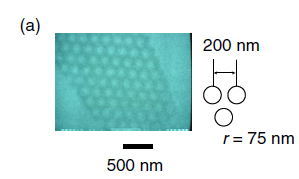
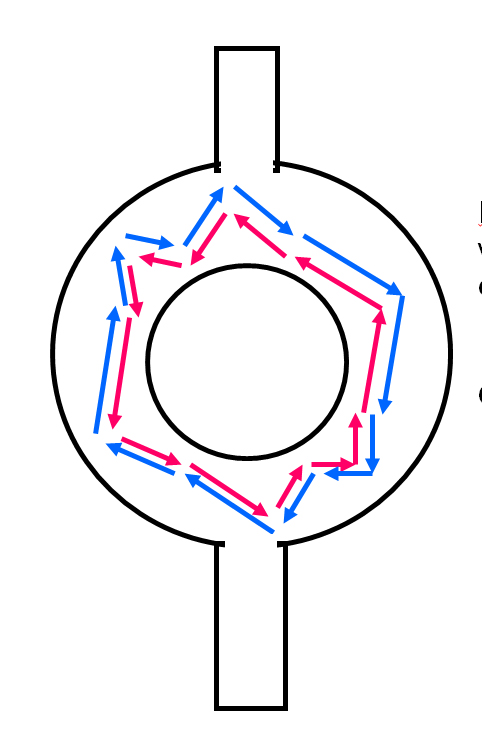
                  SEM of Antidot Lattice Sample.                     A pair of trajectories with time reversal symmetry.

               

 

 

 

 

 

 

 

 

Suspended Graphene

宙吊り構造による高移動度グラフェン素子の作製

　グラフェンの品質向上をするのは、グラフェンの物理の研究のキーポイントです。h-BNを使わなくても、グラフェンの品質（電子散乱の少なさ）を向上させることができます。それは、グラフェンが何にも触れていない宙吊り状態を実現すればいいのです。グラフェンの両端は、基板の上に固定されていますが、その間は、川に渡されたつり橋のように宙吊りになっています。

水などの液体には、分子同士が集まる性質（表面張力）があるので、この構造は作るのがきわめて難しいのですが、私たちは作るのに成功しています。SiO2上にグラフェン素子を形成して、それをフッ酸によってエッチングして作ります。　乾かす時に、表面張力でたいてい壊れてしまいますが、私たちは宙吊り構造を作るのに成功しています。

 Graphene placed directly on the SiO2 substrate is influenced by charged impurity in the substrate. This results in a limitted electronic mobility. Much higher mobility can be attained by suspending.   The image below is a photo of suspended monolayer graphene that was made by us.

              

                  Sem micrograph of suspended graphene. (c) Yagi lab. 

 

 Investigation on the method of graphene fabrication

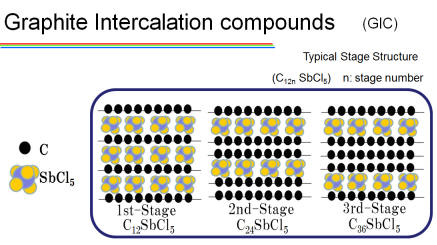
Making Graphene From Graphite Intercalation Compounds   

グラフェンをグラフファイト層間化合物からつくる方法の開発

S. Fukada et al.   Jpn. J. Appl. Phys.  51, 085101 (2012).

　　グラフェンはグラファイトを薄くすることによって原理的には作ることができます。しかしながら、実際に、十分に薄いグラフェンであって、実験などに使えるある程度大きなサイズのものを作るのは容易ではありません。そこで私たちは、グラファイトの層を効率的に剥離するための方法を開発しました。

We can make graphene easily in principle by making graphite thinner and thinner with adhesive tape.  It does not require any special facilities. However it is hard making graphene with a few layer number or less. Sometimes we may not obtain sufficiently thin graphene, and sometimes we may not obtain graphene with sufficiently large sizes by the simple method. How can we overcome it.

　　 グラフェンを作る方法として考えられているのは以下の通りです。テープを用いて力学的に劈開する方法、SiCの熱酸化、CVD法、それから、化学的にグラファイトを酸化して層間をバラバラにする方法です。これら一長一短があります。

 

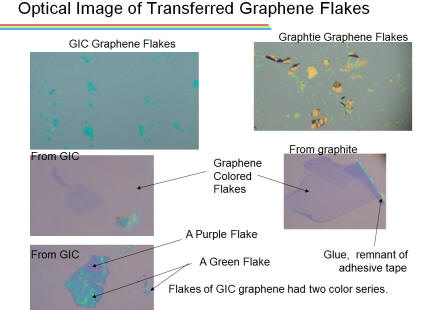
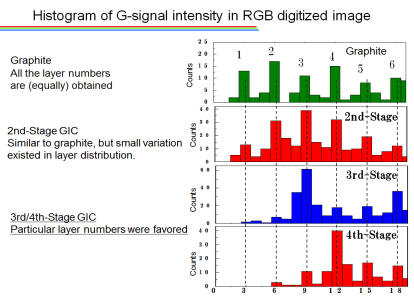
　　 私たちは、力学的な劈開方法を容易にするため、グラファイトをGIC化したところ、剥離の効率が上がりました。しかもステージ数に関連する剥離しやすさがあることを見出しました。　こうして剥離したグラフェンは、GICのドーパンとのため、キャリア密度がきわめて高い可能性が予想されましたが、ほとんどドープされていないことがわかりました。

 

 

 

 

2トポロジカル絶縁体　　Topological Insulators

　トポロジカル絶縁体とは、絶縁体でありながら、表面にグラフェンがついているかのような異常な特性を示す物質です。絶縁体と書いていますが、導電体です。トポロジカル絶縁体の表面にある電子系もグラフェンと同じ質量がゼロの電子（Massless Dirac Fermion）です。しかも、電子の動く向きに電子のスピンの向きが固定されているというとても奇妙な系で、最近発見された新しいものです。

CVD growth of  Bi2Se3 Single Crystal

ビスマスセレン単結晶のCVD（chemical vapor deposition)を用いた作製

　 CVD法と呼ばれる方法で、トポロジカル絶縁体の単結晶成長を行っています。加熱炉に設置した石英管の中に原料と基板を入れ、トランスポートガスを流すことで、蒸発した原料が基板の上に堆積します。条件をうまく選ぶと、単結晶が成長します。

 

この方法でできる単結晶は非常に薄いため、表面の効果を見るのに適しています。下の図は、デバイス形状に加工したサンプルを低温に冷却し、磁気抵抗を測定した結果を表しています。明瞭な弱反局在効果が観測されています。

 

      

 

 

 

3非平衡超伝導

超伝導体中にある非平衡な準粒子状態とその電荷の蓄積効果

 Non-equilibrium superconductivity

 

Observation of charge imbarance of superconducting quasi-particles

R. Yagi  Phys. Rev. B 73, 134507- (2006).

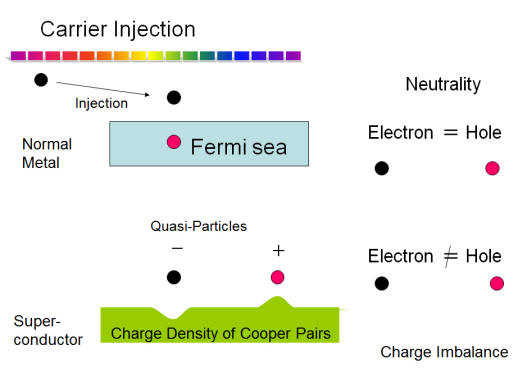
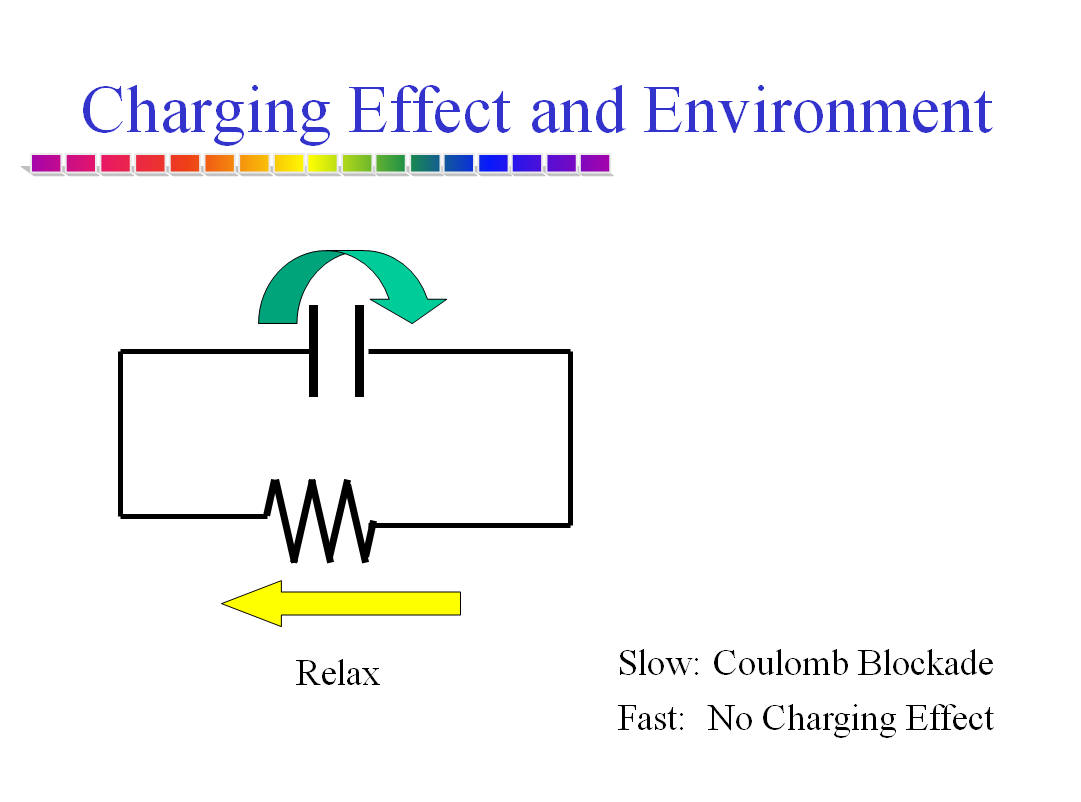
超伝導体には二種類の電子がいる

　超伝導体では、電気抵抗ゼロを担う超伝導電子が凝縮体を作っています。それとは別に、超伝導でない電子がいて、これを準粒子といいます。これは、古くからある二流体モデルと呼ばれている概念ですが、超伝導のミクロな理論であるBCS理論でもこれが妥当であることになっています。超伝導凝縮体の電子数と、準粒子数の比は、温度によって連続的に変わります。これは超伝導状態が二次転移であることを表しています。

　超伝導が一定の温度の熱平衡状態であるとしましょう。そのとき、超伝導体に電気を流すとどうなるでしょうか。ゼロ抵抗なので、超伝導体の中には電場がかかりません。したがって、準粒子は電流を運びません。超伝導の凝縮体がスルスルと動いて電流を運びます。準粒子は電気抵抗としては見えません。

非平衡超伝導体の電荷インバランスとは何か？

　さて、超伝導二つのキャリアがあると書きましたが、これらの電荷にインバランスをつけることが可能でしょうか。つまり、超伝導体が少しプラスの電荷を帯びて、準粒子系が少しマイナスの電荷を帯びるような状態です。もちろん電気的中性から、全部のキャリア密度では中性が保たれていなければなりません。このようなことは、実際におこります。これを非平衡超伝導における電荷インバランス状態と呼びます。

　外から超伝導体に電流を注入すると、すぐには超伝導電子にはなりません。しばらくは、非平衡な準粒子状態になります。一見不可能かと思われるかもしれませんが、この準粒子状態は外から注入した電化と同じ符号の電荷を蓄積することができます。この電荷インバランス状態を、電圧ゼロでも流れる電流として検出しました。

 What is Charge Imbalance of Non Equilibrium Superconductivity?

 Quasi-particles in superconductors are excitations from the ground state of superconducting condensate. They are single particle state.  If you inject electrons into a superconductor, the injected electrons become quasi-particles for a while before they are converted to Cooper pairs or superconducting condensate. Although quasiparticles are single particle state, they are not single particle electron itself, but are  quantum-mechanical superposition of electron and holes. They have fractional charges that depend on ratio of the weight for superposition, which is determined by energy of injection.     superpositions of electron and holes. They have fractional charge because of superposition.

 

 

    

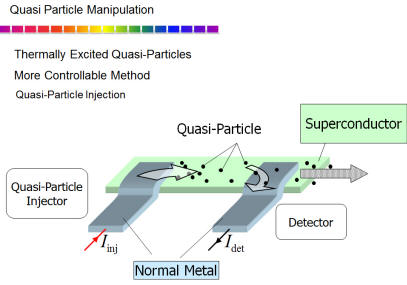
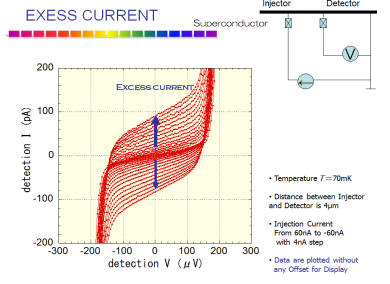
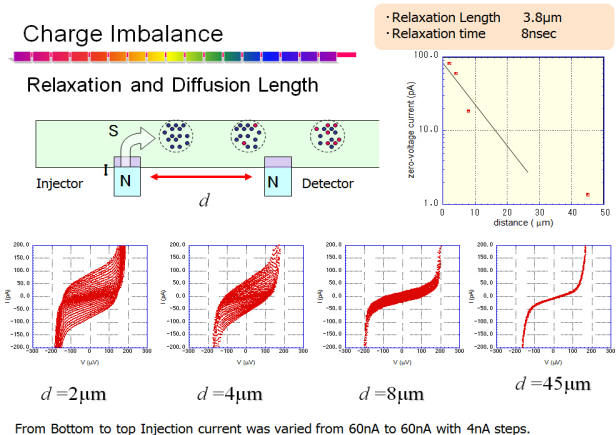
電荷インバランス状態は本質的に非平衡状態です。したがって、時間的に緩和することが考えられます。緩和時間は極めて短いと考えれますので、緩和の様子の時間分解測定を、電子の拡散時間を用いた空間分解測定として観測したのが以下の実験です。超伝導細線にいくつかの検出器（これはトンネル接合）を配置しています。準粒子注入するトンネル接合から遠くになるにしたがって、観測される電荷インバランスは小さくなっていきます。

 

                     

 

 

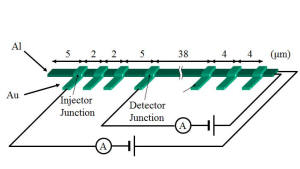
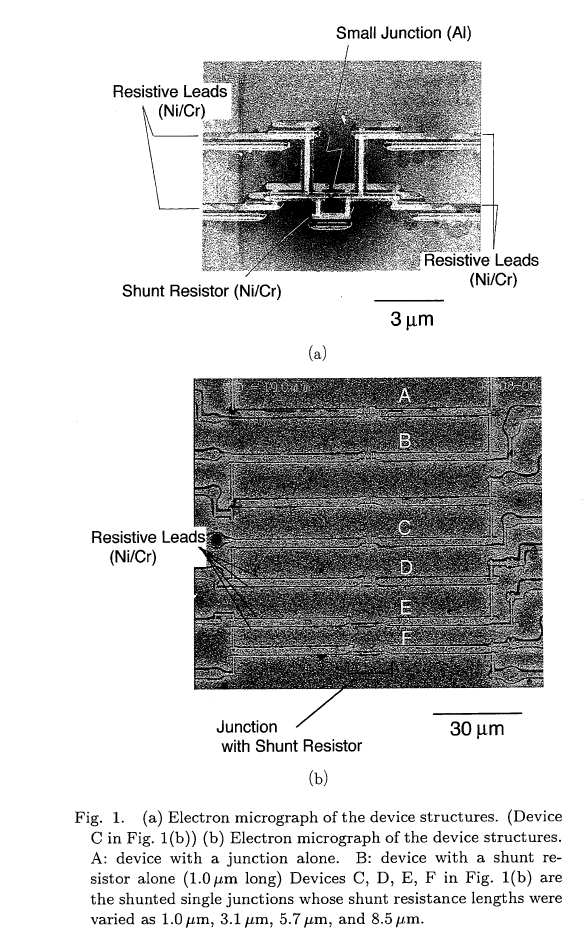
　さて、どのように微小トンネル接合をつくるのでしょうか。　それは割と簡単にできます。二層レジストとななめ蒸着のテクニックを使って作ることができます。二層レジストとしては、PMMAとその共重合体PMMA/MMAの二層構造膜を用いています。現在では、PMMAではなく別のレジストを使う方法も用いています。二層レジストを作ることで、上のレジストが下のレジストよりも残っている構造（アンダーカット）を作ることができ、これを用いると上のレジストがサスペンドされた橋構造がつくれます。異なる二つの角度から金属を真空蒸着をし、蒸着の間に表面酸化をすることでトンネル接合を作ることができます。

Then, how to make ultra-small tunnel junctions?   It is easy.  We used double layer resist and angle oblique evaporation technique.  We made bridge structure that can be formed by the overhang structure of PMMA and the co-polymer resist. Then tunnel junction was formed by depositing metals different angles and oxidation between each evaporation process.

*****************************************

 

 

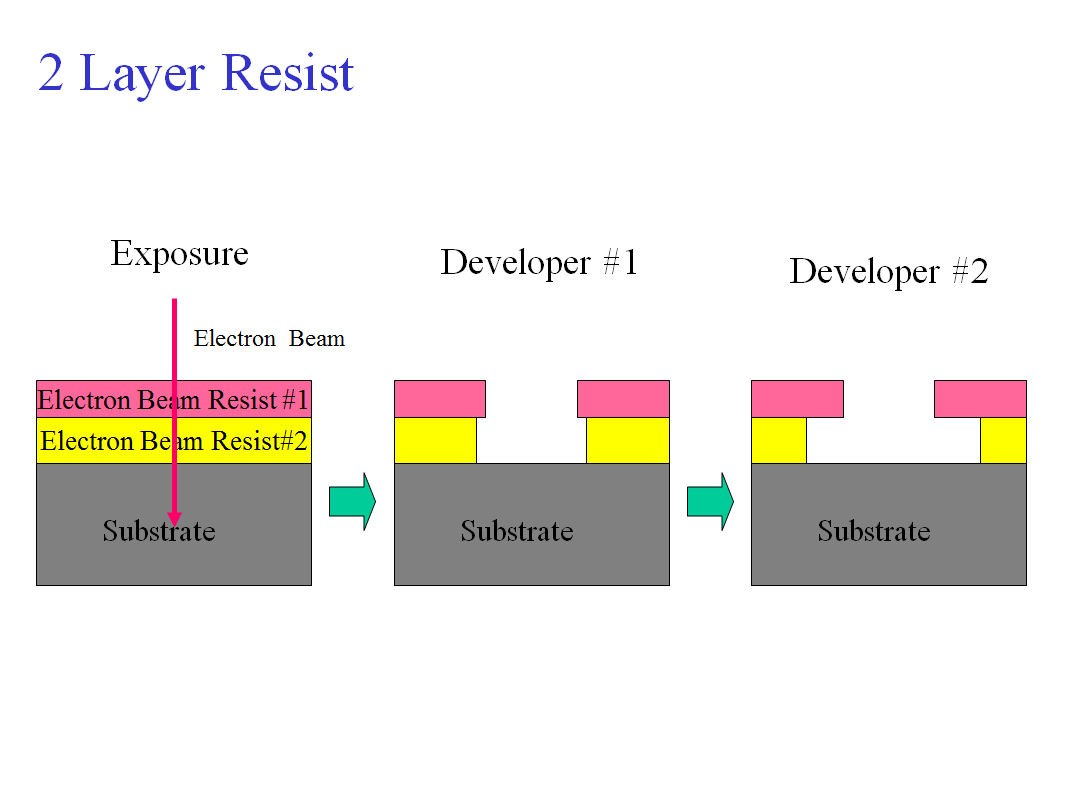
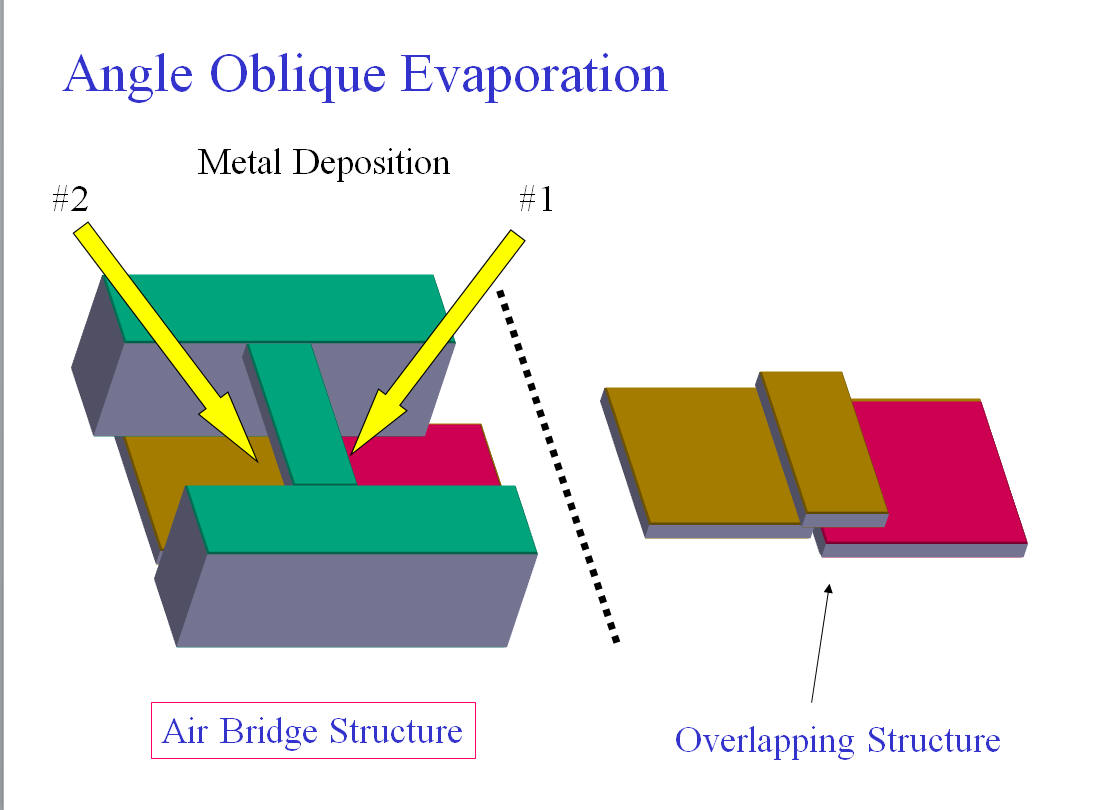
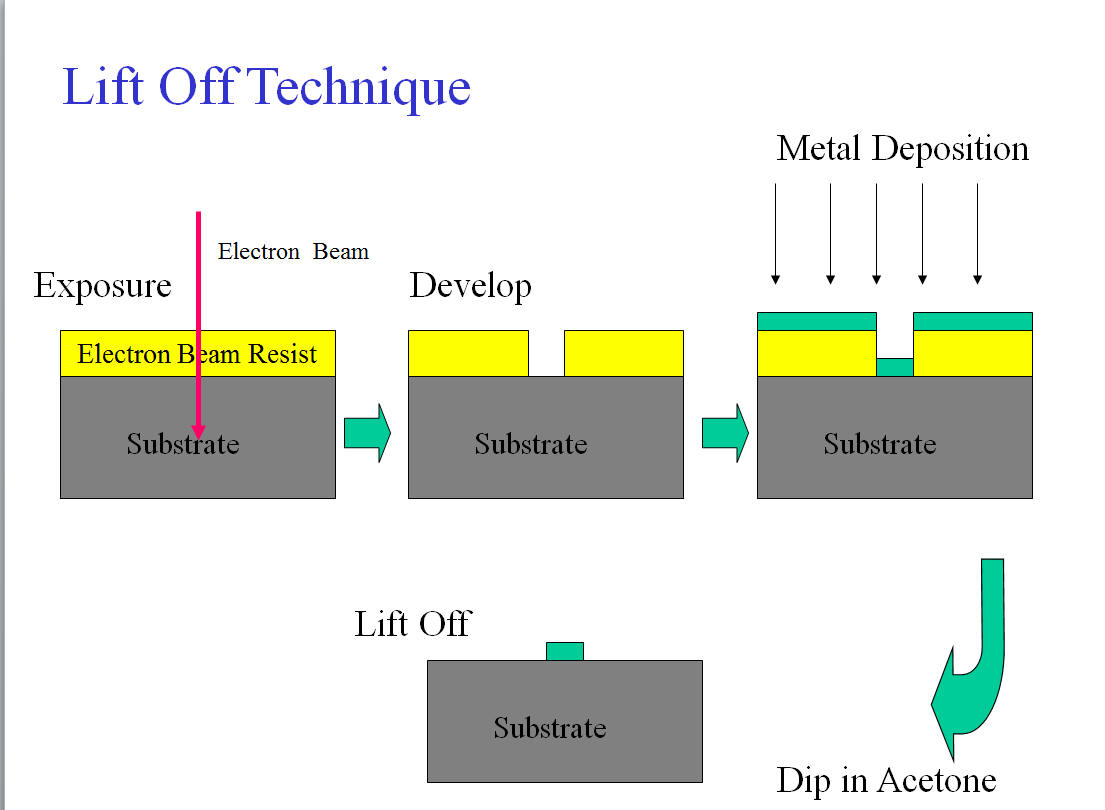
Pair Breaking Perturbation Relaxes Charge Imbalance   

Tsuboi and Yagi,　"Charge Imbalance Relaxation Due to Pair Breaking Perturbation by magnetic field.",

J. Phys. Soc. Jpn. 79, 013704 (2010).

　 超伝導体の中に蓄積している、準粒子の電荷インバランス状態は、電子とホールのコヒーレント量子重ね合わせ状態からなっているので、超伝導や、弱局在と同様に磁場に対して非常に敏感に反応します。その結果、電荷インバランスが磁場の増大とともに急速に減少します。超伝導エネルギーギャップも磁場によって消滅する方向にはたらきますが、電荷インバランスの緩和は、それよりもずっと小さな磁場によって起こる、軌道の効果が表れます。これを初めて観測しています。

　準粒子は、単なる一電子状態ではなく、超伝導状態に由来する量子重ね合わせ状態であることが明確に観測されました。

      

 

 

4 微小トンネル接合

 

Dissipative Phase Transition and Macroscopic Quantum Coherence in Resistively Shunted Small Josephson Junctions 

微小な超伝導トンネル接合の示す、古典・量子境界問題の実験的検証

R. Yagi and S. Kobayashi, J. Phys. Soc. Jpn. 66 3722-3724 (1997).   Takahide Yamaguchi et al. Phys. Rev. Lett. 85 1974-1977 (2000).

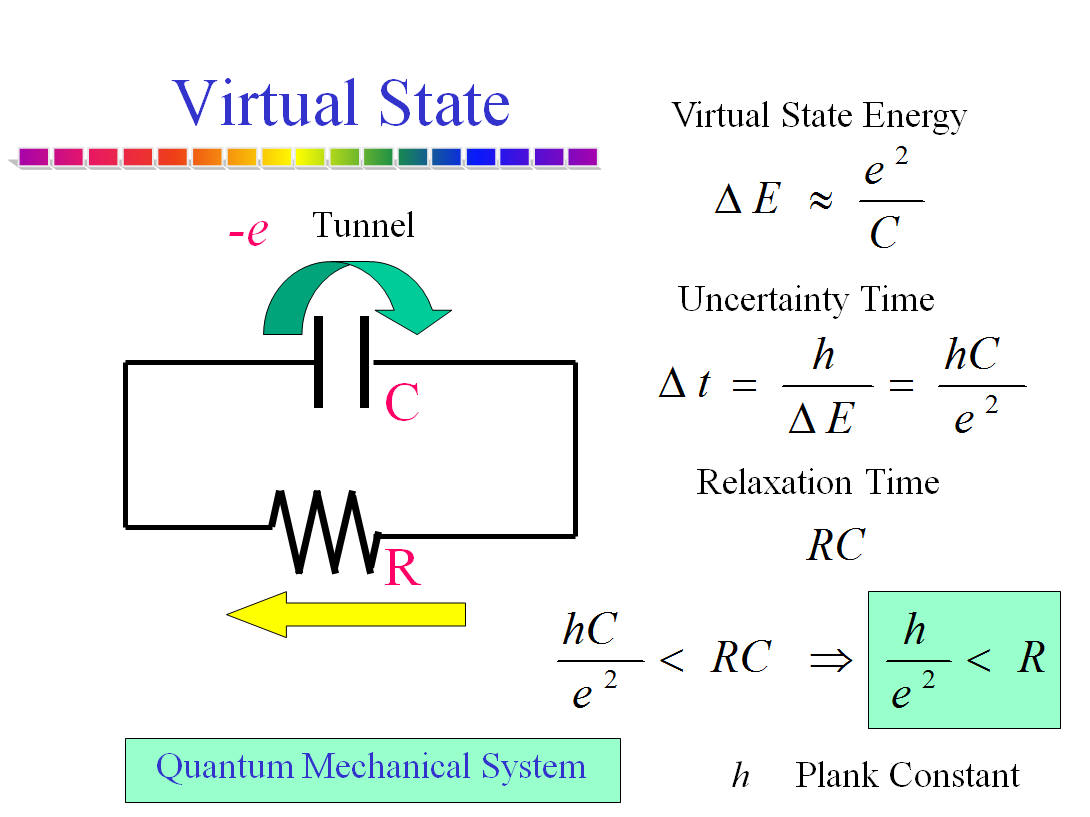
超伝導の超微小なトンネル接合では、シュレディンガーの猫の問題、つまり、マクロな系に対する量子力学効果を研究することができます。

もともと超伝導トンネル接合を、電気回路として見たとき、回路にかかる電圧、回路を流れる電流は、二階の微分方程式で表すことができます。この微分方程式は、ニュートン力学における運動方程式と同形になっているため、超伝導回路の状態方程式はニュートン力学のように求めることができます。　この時、超伝導回路は、古典力学に従い、超伝導電流が流れます。

ここで、超伝導接合のキャパシタンスCは、ニュートン力学における質量mに相当しています。また、超伝導位相θは、ニュートン力学の空間座標xに対応しており、超伝導トンネル接合にたまる電荷nは、ニュートン力学における運動量pに相当します。

ニュートン力学では、質量ｍが十分に小さいときには、交換関係　[x,p]　が無視できなくなり、量子化することになりますが、これと対応する同様な関係、[θ, n]の交換関係が超伝導のマクロ波動関数の性質から期待されるので、回路の状態方程式が量子化されることになります。量子化された回路方程式の固有状態の良い量子数は、nなので、トンネル接合にたまった電荷が観測される状態、つまり、電圧状態が観測されます。つまり、量子化された超伝導回路は、超伝導電流が流れず、電圧状態になり、クーロン閉塞によって絶縁体化することが期待されます。

まとめると、古典領域では超伝導的振る舞い、量子領域では絶縁体的振る舞いを超伝導回路が見せます。

さて、この系で面白いところは、超伝導回路というマクロな系に量子力学を適用できているところです。マクロな系なので、エネルギー散逸を与えることができます。　マクロな量子力学系に散逸を入れた時どのようになるかは、巨視的量子トンネル効果、コヒーレンス効果の最も重要なところであります。トンネル効果を考えると、トンネル確率が低下する向きにはたらきます。そのため、何度もトンネルを繰り返して量子力学的なカップリンングを形成するコヒーレンス効果の場合にも、コヒーレンスが失われる傾向に行きます。つまり、量子力学系は、古典的な系へ向かう傾向を示します。　問題は、どのくらいの散逸のときに、系が古典化する相転移をするかということです。　超伝導接合の場合には、非常に、理論的な考察が進んいて、理論的な予測があります。

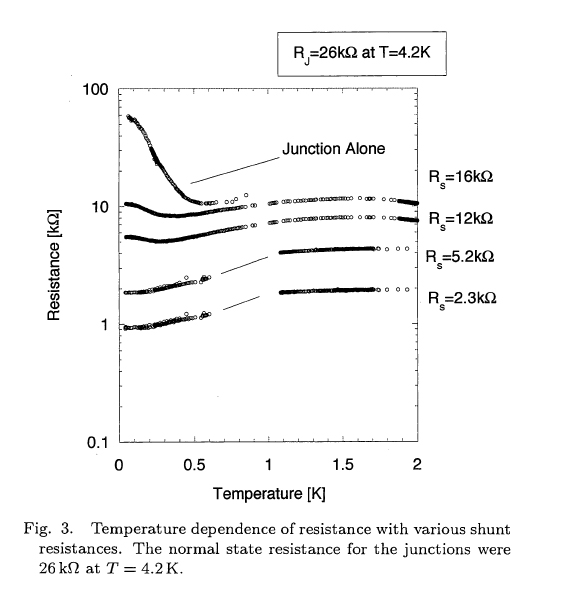
超伝導接合の場合、接合に並列な抵抗を接続することで散逸効果を与えることができます。この抵抗値が量子抵抗h/4e2=6.45kOhmを境として、上では量子力学、下では、古典力学が支配的になる量子相転移が起こります。これは、系が絶縁体としてふるまうか超伝導としてふるまうかという、超伝導絶縁体転移として現れることが期待されます。

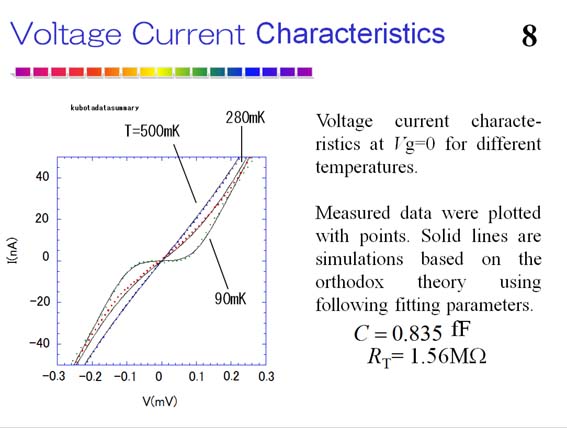
本論文はこれを実際に、ナノテクノロジーを用いて作製し、検証した初めての論文であります。LT２２（低温物理国際学会）で招待講演を行っております。

 

Superconductor-Insulator transition for a single ultrasmall tunnel junction was successfully tuned by external shunt resistor. This is a proof of dissipative phase transition for macroscopic quantum coherence.

                      

 

 

Phase Quantum Bit

Optical and SEM micrograph of phase Quantum Bit. (c) Yagi Lab

 

 

All Chromium Single Electron Transistor                         Kubota and Yagi, Physica B, 383, 57-58 (2006).

常電導金属だけでできた、SETトランジスタ

トランジスタのような増幅やスイッチングの機能がある能動素子は半導体で作られています。しかし、金属だけからなるトンネル接合でも、トランジスタを作ることができます。図のように0.1ミクロン程度以下のサイズの微小なトンネル接合が二つ並んでいる島構造と、近くに延ばしたゲート電極の構造はSETトランジスタ（単電子トランジスタ）と呼ばれます。クーロンブロッケイド効果によって電子の流れを制御することができます。　低温でこのような素子を動作させますが、すべて金属でできたこうした素子は、金属が超伝導になってしまっては話が複雑になってしまうため、都合がよくありません。磁場をかければ常伝導にすることができますが、実際に応用面などを考えれば、磁場なしで動作するのが望ましいと思われます。

低温で、超伝導転移しない金属で作ればいいと言うのは簡単ですが、実際に動作する素子を作るには、それほど選択できる金属がありません。要請されることは、非磁性であること、超伝導転移しないこと、空気中で安定であること、良いトンネルバリアができることです。最後の養成は、トンネル接合のトンネル障壁に関するものですが、この品質がトランジスタ動作の可否を決定づける重要な要素であります。

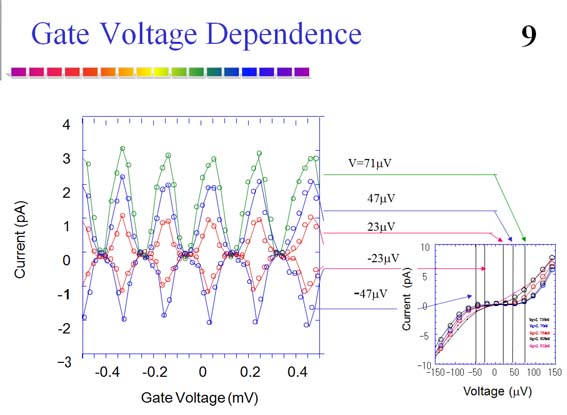
私たちは、クロムを採用しました。クロムは反強磁性的ではありますが、それほど磁場効果が強くあらわれるわけではありませんので、SETトランジスタとして使えそうです。問題は、トンネルバリアの形成ですが、私たちは、酸素プラズマ酸化をすることでトンネル障壁を作ることに成功しました。下の図９は実際ゲート電圧を変えた時のソースドレイン間に流れる電流を示しており、明瞭なトランジスタ動作がみられています。

All chromium single electron transistor consists of metal junctions in normal state even at zero magnetic fields.

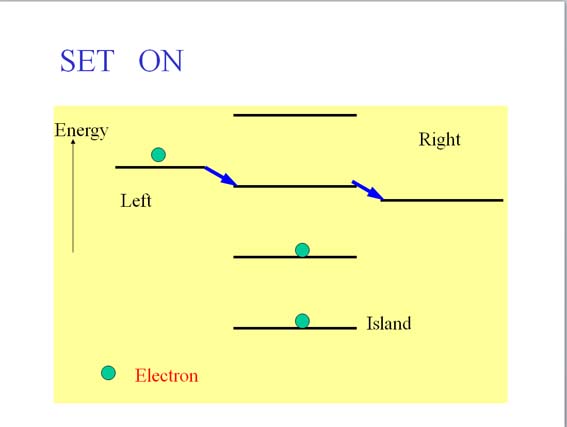
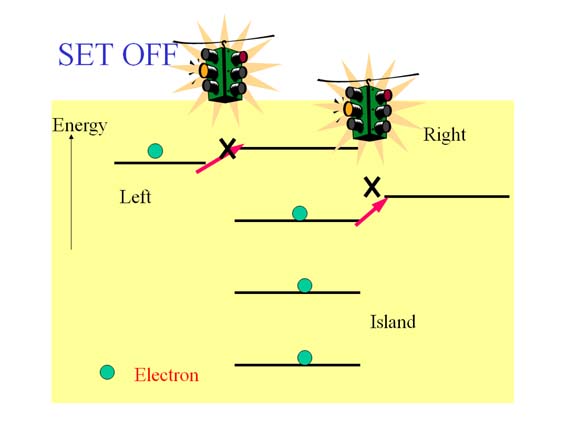
    Principle of Operation 

 

Superconductor- Insulator Transition in Two-Dimensional Array of Josephson Junctions

超伝導微小トンネル接合の二次元アレイにおける超伝導・絶縁体転移

R. Yagi, T. Yamaguchi, H. Kazawa and S. Kobayashi:　"Study on Superconductor-Insulator Transition in Two-Dimensional Arrays of Small Josephson Junctions",　J. Phys. Soc. Jpn. 66 (1997) 2429-2436.

微小なジョセフソン接合が二次元的に結びついたネットワーク（配列）では、位相渦糸と、電荷ソリトンがそれぞれ重要な役割を果たしています。　理想的な場合、Ej>Ec のときには、渦糸系がKosteritz-Thouless （K-T）転移をし、　Ej< Ecのときには電荷ソリトンがK-T転移を起こすことが予想されています。これらは、量子力学的な不確定性から、拮抗する関係にあり、どこか臨界的な値で、熱力学的ではない量子力学的な相転移が起こることが予想されています。これは、超伝導ー絶縁体転移として現れます。

 

 

 

 

Josephson Junction with Tunable Energy Dissipation Using Quasi-Particle Injection

K. Utsunomiya and R. Yagi, 　“Control of Profile of Josephoson Junction by Quasi-Particle Injection“,

Physica B, 383, 53-54 (2006).

 

 

5 幾何学的磁気共鳴効果

Commensurability Magnetoresistance Ocillation

 Magnetic Weiss Oscillation (Theory)    R. Yagi et al. J. Phys. Soc. Jpn., 62 1279-1285 (1993).

空間的に磁場の強弱があるときに、量子系はどのようにふるまうか。その問題に取り組んだものが本論文です。一様な磁場の下で、洗濯板のような磁場変調を空間的に配置したとき、電子系は下の図のようなエネルギースペクトルになることが示されました。これは、変調磁場周期と、電子サイクロトロン運動の間の整合性によって磁気抵抗が出ることを意味しております。

                                       

 

 

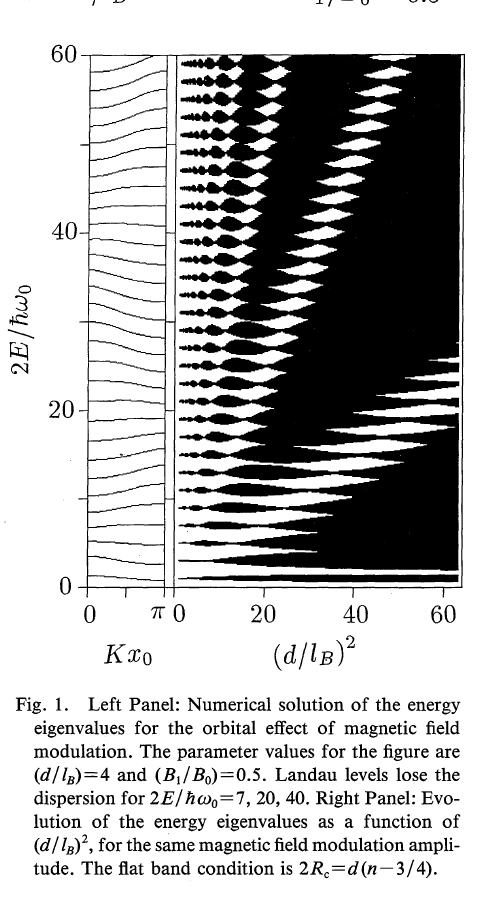
Quasi-Two-dimensoional Electron System

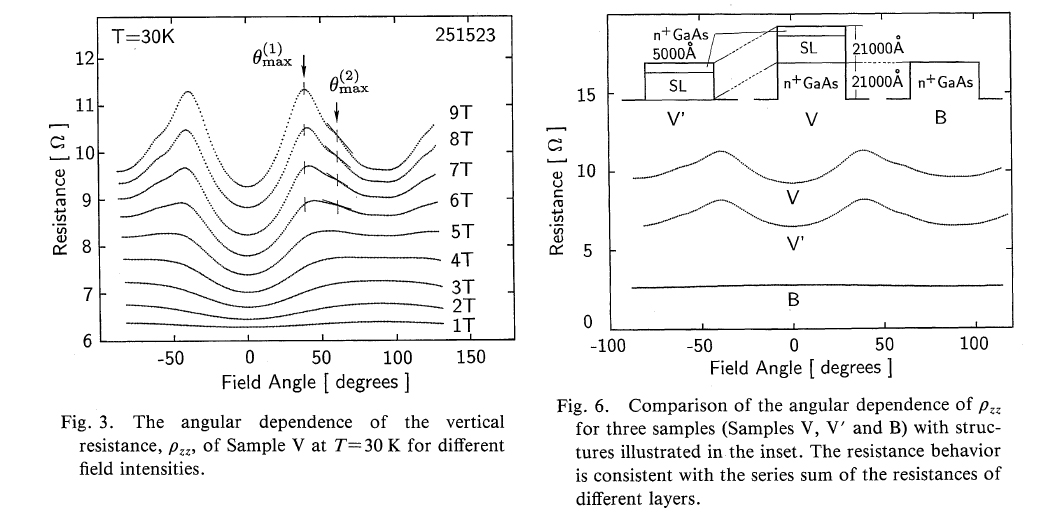
Angular dependent Magnetoresistance Oscillation (AMRO) in quasi-two dimensional electron systems.

Semiclassical Transport Theory of AMRO.    R. Yagi et al.  J. Phys. Soc. Jpn. 59  (1990) 3069-3072.

層状物質に磁場をかけた時に磁気抵抗が磁場の角度として振動が起こるという現象がAMRO効果です。

このAMRO現象が発見された直後に、その磁気抵抗起源について解明したのが本論文です。当時、K.Yamaji氏が、ある磁場角度で二次元化が強く起こるというアイディアを提唱したのですが、振動の本質がまだわかっておらず、熱心に議論が行われておりました。

本論文で、AMRO振動がボルツマン　輸送現象の範囲で出ることが示されました。そして、面直方向の抵抗に主にAMRO振動が出ることを予言したものです。

AMRO振動は、今ではさまざまな物質のフェルミ面形状を決定するのに用いられています。　今までに、有機導体、高温超電導体、p波超伝導体候補物質、半導体超格子、グラファイトインターカレーションなどでも観測されています。

 

 

 

  

 

 

 

 

 

 

 

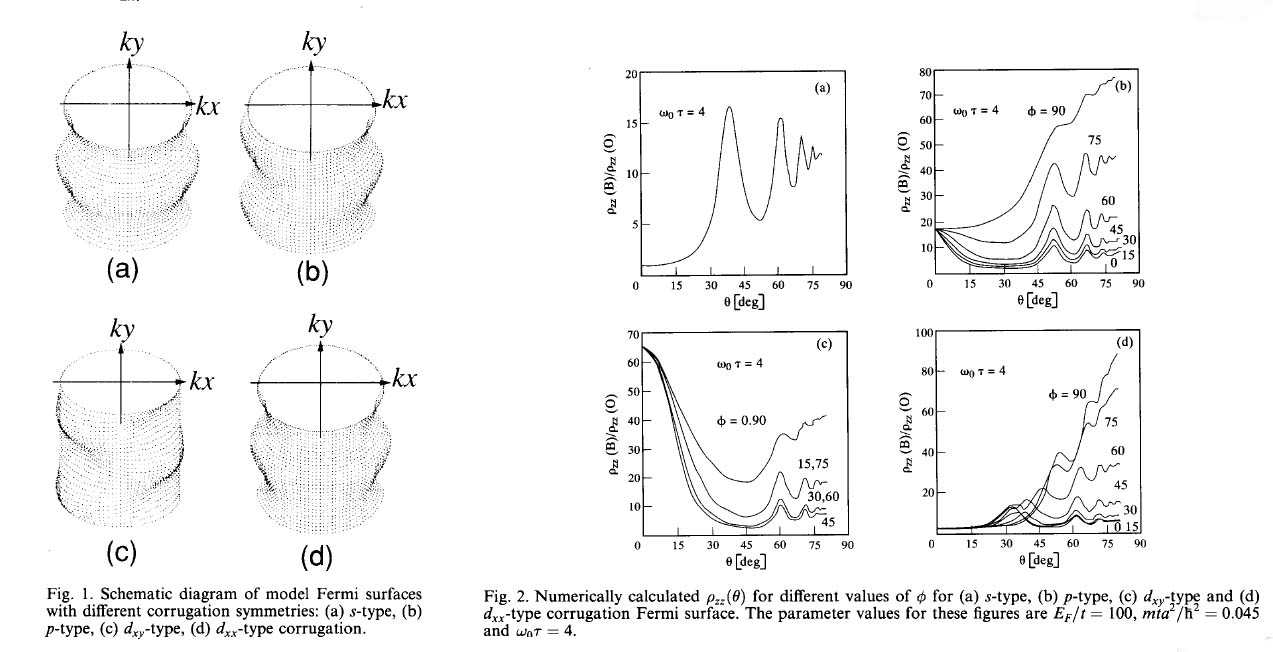
AMROs for various fermi surface shapes.     R. Yagi and Y. Iye, Solid State Commun. 89(1994)275-281.

          

  AMRO in Semiconductor Superlattices         R. Yagi et al.    J. Phys. Soc. Jpn. 60(1991) 3784-3791.

この論文は、AMRO効果がまだ、有機導体でしか観測されていない時期に、その一般性を示すために半導体超格子でフェルミ面を設計して実際にAMRO振動を観測するのに成功したものです。磁気抵抗ピークが二つしか見えていませんでしたが、その後、強い磁場のでる超伝導磁石で測定をしたところ、数多くのピークが観測されています。

本論文は、同時に、AMRO効果の異方性、つまり、面直方向に振動が主に出ることを実験的に証明したものです。

      The first observation of AMRO in systems other than organic conductors. 

 

 

 

On the Temperature Dependence of the Hall Resistance in Low Carrier Density Metals

R. Yagi and Y. Iye, J. Phys. Soc. Jpn 61,227(1992)

ホール効果はキャリア密度を直接測ることのできる有力な手段です。しかし、キャリア密度がちいさく、フェルミエネルギーが小さな金属の場合には、低磁場領域で測定したホール抵抗が温度依存性を示す場合があります。

これを、GaAs/AlGaAsの半導体超格子で調べました。低温になると、量子振動（シュブニコフドハース振動）から見積もられるキャリア密度は減少するのに、低磁場で測定したホール効果から見積もられるキャリア密度はむしろ増大しているように見えます。　抵抗の温度依存性を見ると、キャリアが減っているように見えます。

このパラドックスのようなことは、実は弱磁場ホール効果が、ホールファクターと呼ばれる散乱のエネルギー依存性の分だけ修正を受けていることが原因であることが半定量的に明確に示されました。

 

 

 

                                

Electron Beam Writer       Ultra Small Metal Ring to observe AB Effect        Single Electron Transistor