| Integrated Profiles Method(IPM)の特徴−2 |
| IPMのその他の特徴をいくつか挙げてみましょう。 |
| ・Double-exponential型のprofileで,riseとfallの速度差をまったく気にする必要がない。
このことには,具体的にOHのprofileを示したページでも少しふれましたが, |
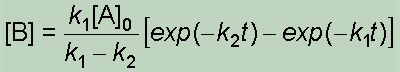 |
| という関数形はk1 ≒ k2という状況では使えませんが,IPM解析式 |
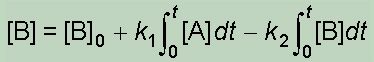 |
| は,k1 = k2という状況でも安全に使えます。 |
| ・Double-exponential関数はk1とk2に関する2価関数だが,IPM解析式では,1価である。
Double-exponential関数は,riseとfallのうち早い過程の方が常にriseに現れ,k1,k2とrise,fallの対応関係は一義的には決まりません。(つまり,k1とk2を入れ替えても成立することになります。)従って,k1とk2の大小関係が既知でなくてはなりません。一方,IPM解析では,k1とk2に関して入れ替えは不可能ですから,k1とk2は一義的に決定でき,また,k1,k2の大小関係が未知であってもまったく問題がありません。この辺の詳細およびIPMのその他の特徴に関しては,論文を参考にして下さい。 |