
Last update : July 28, 2010
| 日程 | : | 2010年7月10日(土) |
| 場所 | : | 東京都千代田区外神田1-18-13 |
| 秋葉原ダイビル12階 首都大学東京 | ||
| 「秋葉原サテライトキャンパス会議室D」 | ||
| 講演者 | : | 橋本 義武 氏 (東京都市大学知識工学部) |
| 講演題目 | : | 「共形場理論の幾何」 |
| 酒井 高司 | (首都大学東京理工) |
| 田崎 博之 | (筑波大学数理物質) |
| 小野 肇 | (東京理科大学理工) |
| 黒須 早苗 | (東京理科大学理) |
| 13:30-14:30 | 「Harish-Chandra pair と D 加群」 | |
| 15:00-16:00 | 「安定曲線の族」 | |
| 16:30-17:30 | 「頂点代数からカイラル代数へ」 |
1.Harish-Chandra pair と D 加群
Lie 環の表現のうち,Lie 群の表現からくるものは,
Lie 群の作用する空間の幾何によって,詳しく調べることができる.
Harish-Chandra pair の理論では,Lie 環の表現で,部分 Lie 環への制限が Lie 群の表現からくるものを考える.
このとき用いられるのが D 加群の言語である.
共形場理論は,無限次元 Lie 環に対する Harish-Chandra pair の理論として定式化される.
2.安定曲線の族
共形場理論の舞台である,無限次元 Lie 環の作用する空間は,
点つき安定曲線(退化を許した Riemann 面)の族である.
点を増やしていくと空間の塔ができる.
共形場理論は,この塔の上の D 加群の構成という形で展開する.
3.頂点代数からカイラル代数へ
共形場理論の出発点は,頂点代数とその表現である.
頂点代数は,いろいろな無限次元 Lie 環の表現のもつ構造を公理化したもので,
安定曲線の族の上の D 加群を誘導する.
頂点代数は形式的 Laurent 級数を用いて定義されるが,これを層の言語に翻訳すると,
カイラル代数の概念に導かれる.
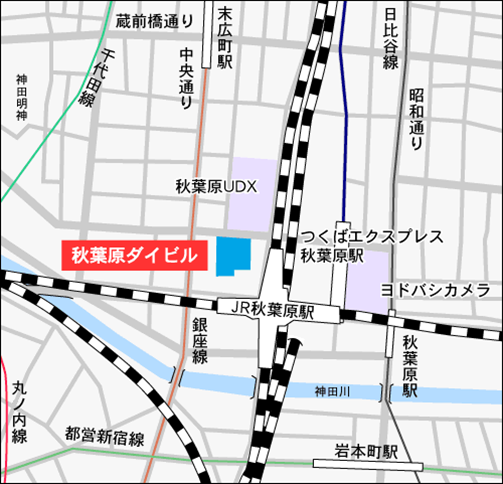
| JR 山手線・京浜東北線・総武中央線 | 「秋葉原駅」 | 徒歩約1分 |
| つくばエクスプレス | 「秋葉原駅」 | 徒歩約2分 |
| 東京メトロ日比谷線 | 「秋葉原駅」 | 徒歩約5分 |
| 東京メトロ日銀座線 | 「末広町駅」 | 徒歩約5分 |

問合せ先: 酒井 高司 sakai-t (at) tmu.ac.jp