コンテンツ

第１２回

連結バネ系

前回、前々回と偏微分方程式の数値解法について演習を行いましたが、今回は今一度オイラー法とルンゲクッタ法を用いた数値解法に取り組みます。
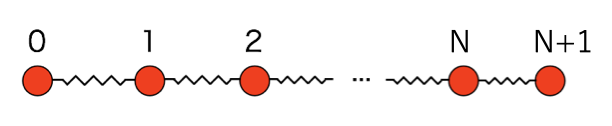
今回は、次のように x 軸上にバネを並べ、おもりでつなげた場合どのような運動をするか、数値的に計算してみましょう。
ただし、全てのバネの自然長 R (伸びも縮みもしていないときの長さ)とバネ定数が同じで、おもりの質量も同じとします。

左のおもりから順に 0, 1, …, N, N+1 と番号を振ります。
全てのバネが伸びも縮みもしていない状態であれば、j 番目のおもりの位置はバネの自然長 R を用いて、j*R と書けます。
これを用いると、j 番目(j ≠ 0, j ≠ N+1)のおもりの運動は、j*R からのズレ $y_j$ を用いて次のように書けます。

(1) $\begin{equation*}\left\{ \begin{array}{l}\ddot{y}_j(t) = -\omega^2(y_j(t) - y_{j-1}(t)) - \omega^2(y_j(t) - y_{j+1}(t)) = \omega^2(y_{j-1}(t) - 2 y_{j}(t) + y_{j+1}(t)) \\y_j(0) = 0 \\\dot{y}_j(0) = 0\end{array}\right.\end{equation*}$

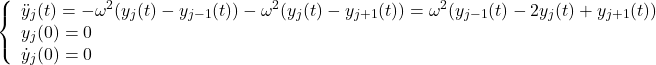
0 番目と N+1 番目のおもりは固定されて動かないとします。つまり、

(2) $\begin{equation*}\left\{ \begin{array}{l}y_0(t) = 0 \\y_{N+1}(t) = 0 \\\dot{y}_0(t) = 0 \\\dot{y}_{N+1}(t) = 0\end{array}\right.\end{equation*}$

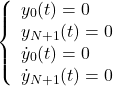
とします。

実際には、 $y_j(t) = y_j(t), \dot{y}_j(t) = v_j(t)$ とした2(N+2) 個の連立微分方程式に対し、オイラー法（できればルンゲ・クッタ法）を利用します。

補足：第八回のバネの伸びの方程式から式(1)がでてきます。
$y_j$ をおもりの場所そのものとしても式(1)と同じ方程式になることと合わせて確認してみてください。

オイラー法でのアルゴリズムを下に示します。ルンゲ・クッタ法ではどうすればよいかは各自考えてみてください。

アルゴリズム

解を求める時刻の上限を $T$ とし、適当な自然数 $M$ を定めて $\tau=T/M$ とする。
（もしくは先に $\tau$ を定めて $M=int(T/\tau)$ とする。）
$y_j$ を配列変数 Y[j] で， $v_j$ を配列変数 V[j] で表す.
(配列 Y[N+2], V[N+2], Y_new[N+2], V_new[N+2]は実数型配列。)
T, τ, t 及び関数 f1(t, x), f2(t, x1, x2, x3) は実数型
M, N, k, j は整数型(int)

必要なライブラリの読込
T, τ, M, N, R, ω (w 等で代用)を設定
YとVおよびY_newとV_newをnp.zerosを用いてM+2個の配列として初期化する
（１. 初期値を与える）
V[1]=0.25（課題１での初期値の設定）
t = np.linspace(0, T, M+1)
f1とf2の定義
（２. 計算）
(時間方向への繰り返し)
k = 0,1,2,.......,M の順に (for 文）
    
    （おもりの描画）
    一定間隔毎に(例えば k%100==0 の時に, 等)
        j = 0, 1, 2,...., N+1 番目のおもりと線を描画（おもりの位置はj*R+Y[j]）
        少しの時間停止
    
    （次の時間でのおもりの位置を計算）
    j = 1,2,.......,N の順に (for 文）
        Y_new[j] = Y[j] + τ*f1(t, V[j])
        V_new[j] = V[j] + τ*f2(t, Y[j-1], Y[j], Y[j+1])
    を繰り返す
    
    （データの更新 (全てのおもりについて計算)）
    j = 1,2,.......,N の順に (for 文）
        Y[j] = Y_new[j]
        V[j] = V_new[j]
    を繰り返す
を繰り返す

f1(t, x), f2(t, x1, x2, x3) は関数として定義

描画の時間間隔やpause関数の時間を適度に調整して、滑らかな動きが見えるようにしてください.

課題１

N=1、ω=1、R=1 として、式(1)と式(2)をとくプログラムを作成せよ。ただし初期条件は、 $y_1(0)=0$ 、 $v_1(0)=0.25$ とする。
オイラー法の場合, 時間刻み幅は τ=0.0001 (T=300等)として、1000ステップ毎に、おもりの位置 (j番目のおもりの位置は $(j*R + y_j(t), 0)$ を ○で表示させること。

（ルンゲクッタ法の場合, 時間刻み幅は τ=0.01 として、10ステップ毎に、おもりの位置 (j番目のおもりの位置は $(j*R + y_j(t), 0)$ を ○ で表示させること。）

次図ではグラフにする横軸の範囲は[0, 2]とした。
また下のアニメーションはファイルサイズ軽減のためT=31.4としているので注意。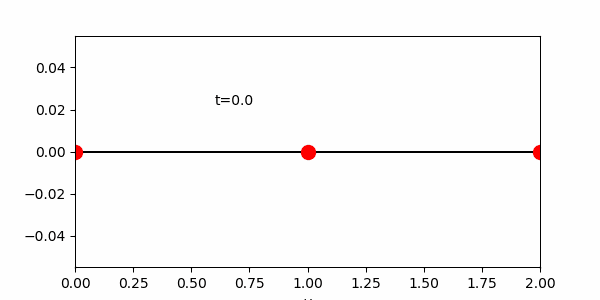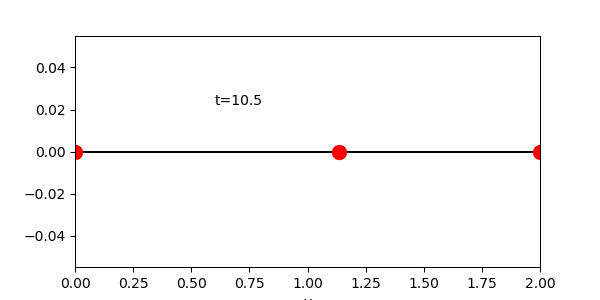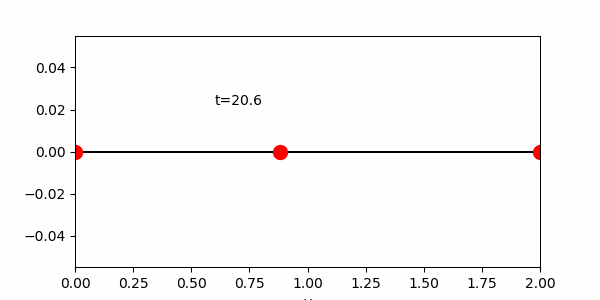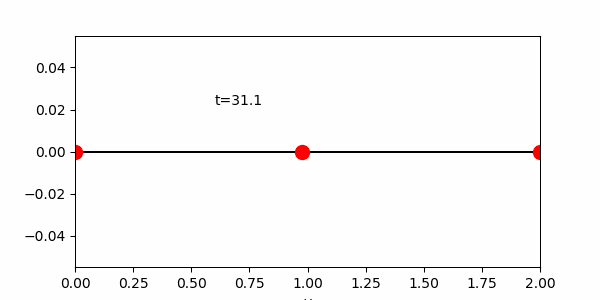

課題２

課題１のプログラムを N = 3, 10 にしてその様子を見よ。v₁=0.7、それ以外の $y_j, v_j$ は0を初期条件とする。（グラフの横軸の範囲は [ 0, (N+1)*R ] とする.）

課題３

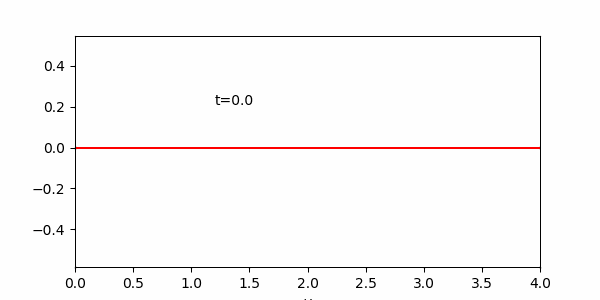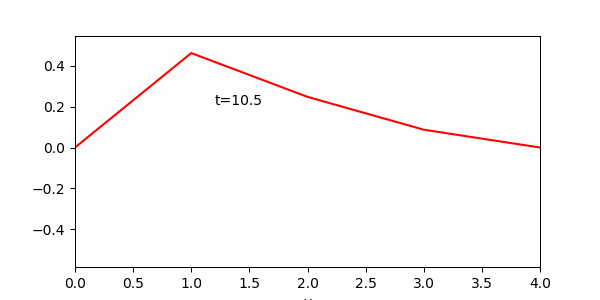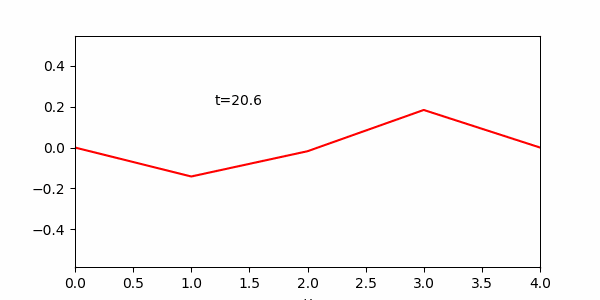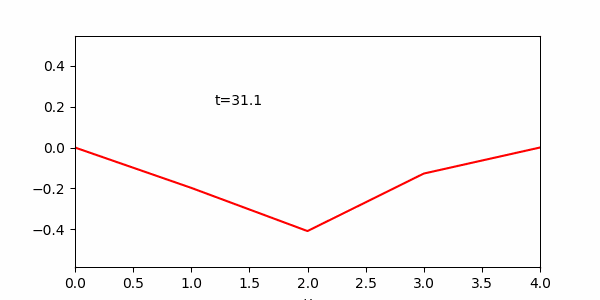
課題２のプログラムのグラフ表示部分を、点 $(j*R, y_j)$ を直線で結ぶように書き換えよ。また, N をさらに増やした場合の様子を見よ. （グラフの縦軸の範囲は [ -0.5, 0.5 ] 等）

また下のアニメーションはファイルサイズ軽減のためT=31.4としているので注意。

課題４

課題３のプログラムをルンゲ・クッタ法を用いて書き直せ。時間刻み幅は τ=0.01 として、10ステップ毎に、おもりの位置を表示させること。

課題５

N= 10、 $v_1=0.7$ 、それ以外の $y_j, v_j$ は0を初期条件として、
次の二つの図を上下に表示させ、アニメーションを行うプログラムを作成せよ。
上の図：課題２と同様の図
下の図：課題３と同様の図
ただし、数値計算の方法はルンゲ・クッタ法であるとし、時間刻み幅はτ=0.1であるとする。

小ネタ：連結バネ系について…

あらゆる物質は分子、原子（厳密には素粒子ですが）から出来ています。
そのうち「固体」と呼ばれているもの（氷等の結晶や金属等）は、そのような分子（原子）間に働くの引力と斥力によって、あたかもバネで繋がれたかのように、それらが規則正しく（等間隔に）配置されている状態であります。（この「バネ」という比喩は実際の分子によく合致します。)
ですので今回の課題２、３は、このような「固体」を原子レベルで見たような事になっています。（厳密には違いますが、大まかに…)
ω によってその「固体」の固さが変わる感じです。
課題２、３では波のようなものが見えていたかと思いますが、この波が空気に伝搬して耳に入ると「音」として我々が認識することになります。
そういえば昔、量子力学用語の解説として「世の中〜波で出来ている〜」と踊っていた人がいたとかなんとか…

発展問題

今回の課題について、おもりに関するfor文を使わずに（ベクトル演算を使って）プログラムを書け。

小ネタ：ベクトル演算

例えば、N+2個の配列 y, z に対して

for j in range(1, N+1):
   z[j] = (y[j-1]+y[j]+y[j+1])/3

として3近傍の移動平均を計算する場合、

z[1:-1] = (y[0:-2]+y[1:-1]+y[2:])/3

と書いてやれば、ベクトル演算となり、for文を使わなくてもよくなります。また、実は関数の仮引数はベクトルでも良く、また戻り値も同様です。

このようなベクトル演算は、プログラムの可視性を上げたり、並列計算をするときなどに効率がよくなるという利点もあります。（科学計算ソフトウェアのMATLABなどは、for文の実行速度が非常に遅く、ベクトル演算できる部分はベクトル演算にしないと非常に計算効率が下がります。）

また（この授業で散々Pythonを使って微分方程式を解かせておいてアレですが）、Pythonの最大の強みはデータ解析のライブラリが豊富なことです。集計や関連性の解析や機械学習など、手軽に様々な解析ができるようにライブラリが作られていますし、何より無料で使えます。
データもいわばベクトルや行列の形式です。ベクトル演算・行列演算ができればプログラムは非常にすっきりします。

一度作ったプログラムを見直し、ベクトル演算できるところを探してみてはどうでしょうか？

Masashi FUJII

計算数理A演習第12回