コンテンツ
第１４・１５回
期末レポート
次の問題のいずれかを選び、提出せよ。なお、それぞれ最大となる点数が異なるので、注意すること。両方提出した場合は、点数の高い方を採用する。
これまでのレポート問題とあわせて総合的に判断しますので、とにかく出すようにしてください。
問題1（最大20点）
次の初期値境界値問題を数値的に解き、アニメーションを作成せよ。
(1) 
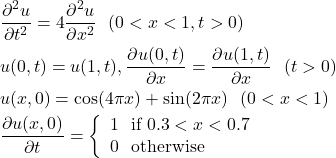
問題1の注意事項
- 空間刻み幅h=0.01とする
- シミュレーション終了時刻T=10とする
- 時刻0.01ごとに描画し、時刻tをグラフに記載すること
- グラフの横軸・縦軸を記載すること
- グラフのタイトルに学生番号を記載すること
- アニメーションに
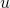の空間方向の平均値である
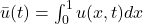を次のいずれかの方法で記載すること
- 値を文字列として描画（時刻と同様の方法）
- グラフとして、[0,1]の範囲で点線で描画（x軸に平行な線が動く）
- プログラムの先頭に学生番号氏名を記載すること
問題2（最大40点）
拡散方程式、反応拡散方程式、連結バネ系、波動方程式について、様々な応用研究がなされている。各自どのようなものがあるか調べたり、自分自身で現象を考え、プログラムを書け。モデルの説明や予測・背景と、そこから得られる結果を考察し結論を述べ、PDFファイルにまとめよ（目安として最小1ページから最大4ページ程度）。
問題2の例
- Gray–Scott 方程式について
- タンパク質のモデルについて（簡単な系）
- 暖房設置時の温度勾配について
- 波動方程式による津波の表現
などなど
採点基準
- プログラムは正しくかつわかりやすく書けているか
- PDFファイルは読みやすく工夫しているか
- 現象への着眼点や考察のユニークさ
- 対象やその背景について、文献などを適切に引用して調べているか
- 結果について図やデータを交え、客観的かつ科学的に考察ができているか
問題2の注意事項
- 計算コストに関する難易度（たとえば計算に3日かかるなど）は採点には影響しません。
- 対象が複雑な場合は簡略化しても構いません（当然パソコンのスペックによっては無理なものもありますので）。
- 参考にしたホームページや論文・書籍などは必ず正しく引用すること。
- 助言をくれた人、手伝ってもらった人には謝辞を書くこと。
- グループワークのように共同で書いても構いませんが、どこを担当したのか明記すること（論文でいうと、coauthorがいる場合はAuthor Contributionを書く、ということ）。
また、PDFファイルは同じものを、プログラムはそれぞれが作成したものをアップロードすること。
（ただしグループワークの場合は、人数が多ければ多いほど高いクオリティを要求します。） - 余裕がある人は、短い論文を書く気持ちで、「背景」「モデル」「結果」「結論と議論」の4部構成で書いてみてください。実際に過去の論文などをGoogle ScholarやCiNiiなどで調べてみると雰囲気がわかります。
提出期限・方法
2025年6月8日（日） 23:59（日本時間）までに、
- PDFファイル（問題1のみの場合は不要）
- レポート作成に使用した拡散方程式・反応拡散方程式・連結バネ系・波動方程式の（いずれか、または、複数の）数値解法を含むプログラム
をmoodleから提出。
最終成績について
最終成績は、
- 小レポート：各20点×3
- 期末レポート：最大20点 or 40点
の合計で決まります。
moodle上では、各小レポートの点数は100点満点換算、期末レポートは40点満点で記載しています。
90点以上は秀、80点以上は優、70点以上は良、60点以上は可、60点未満は不可とし、小レポートも期末レポートも1度も提出されていないものについては欠席とします。