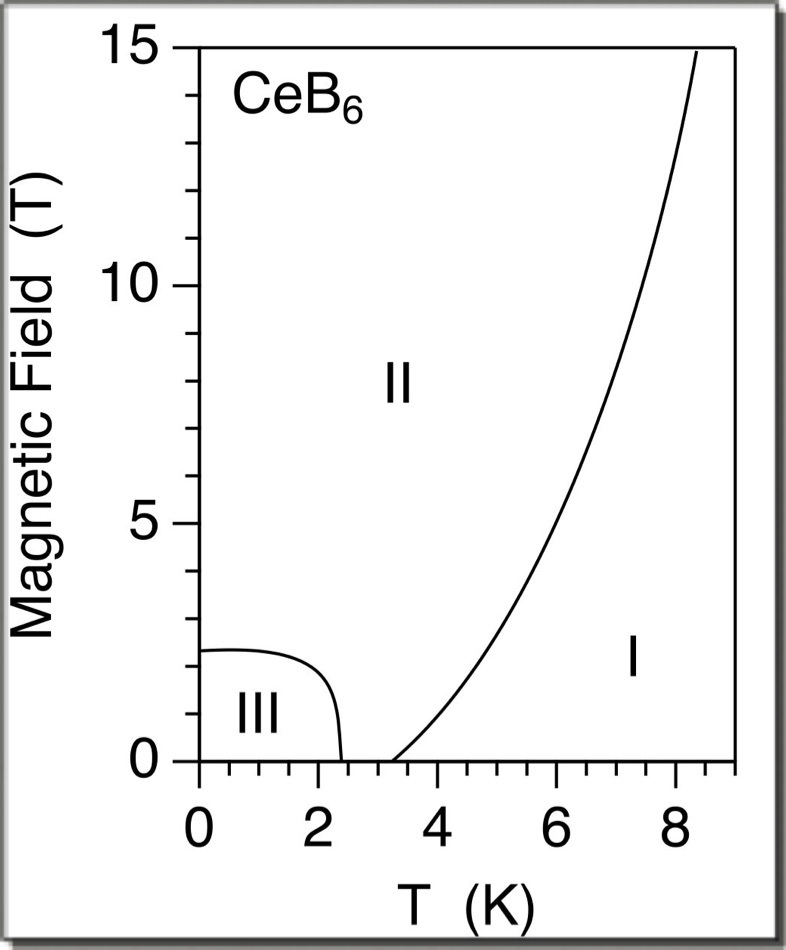
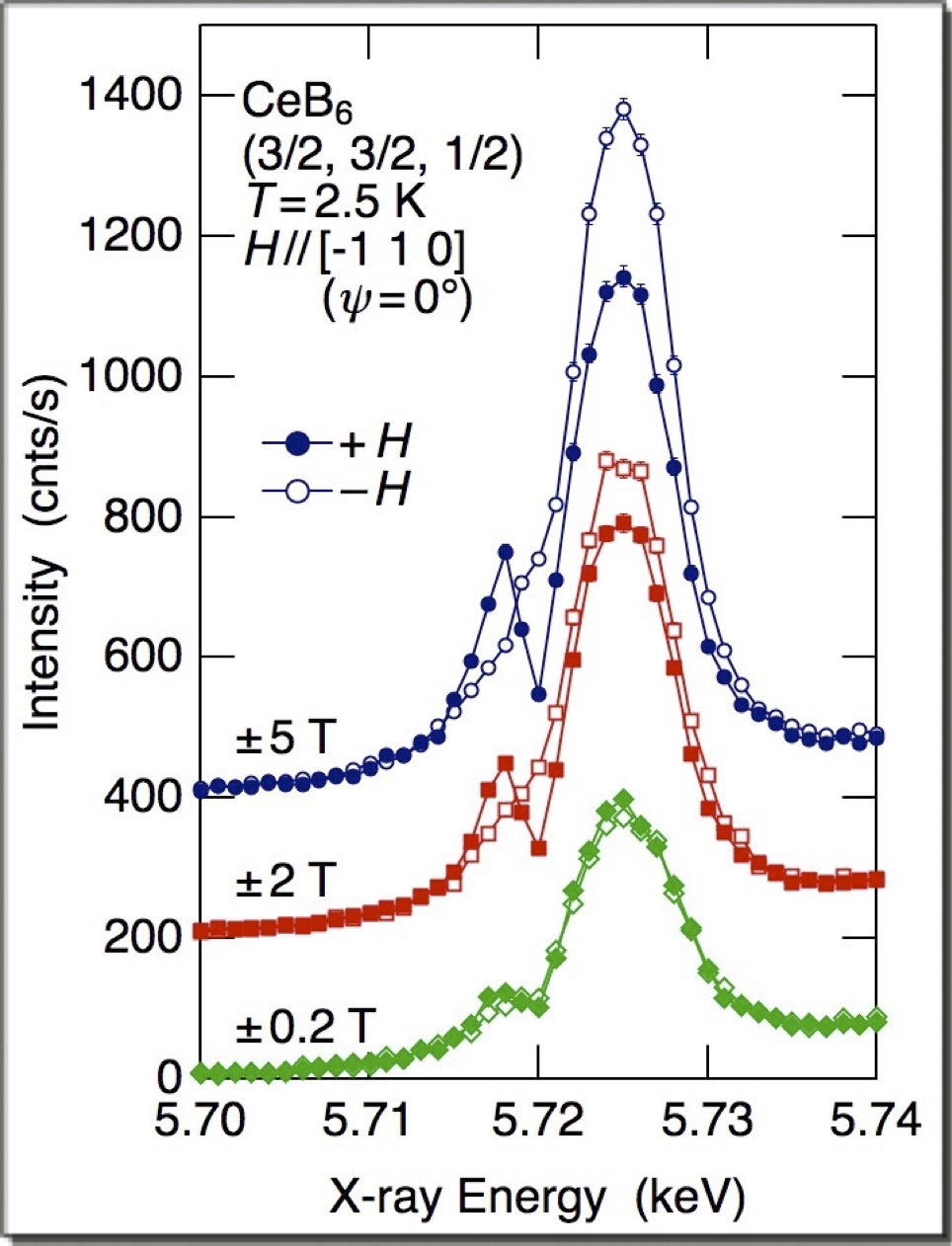
【1】CeB6の磁気相図．I相は常磁性相，II相は反強四極子秩序相(AFQ)，III相は反強磁性秩序相(AFM)．

【4】2.5 K (AFQ相)，[-110]方向の磁場中での，(3/2, 3/2, 1/2)Bragg反射強度のエネルギー依存性（PRL論文のFig. 1）．磁場方向を反転させるとE1共鳴(5.724 keV)とE2共鳴(5.718 keV)での強度が変化する．吸収補正なし，バックグラウンド差引きなしの生データ．

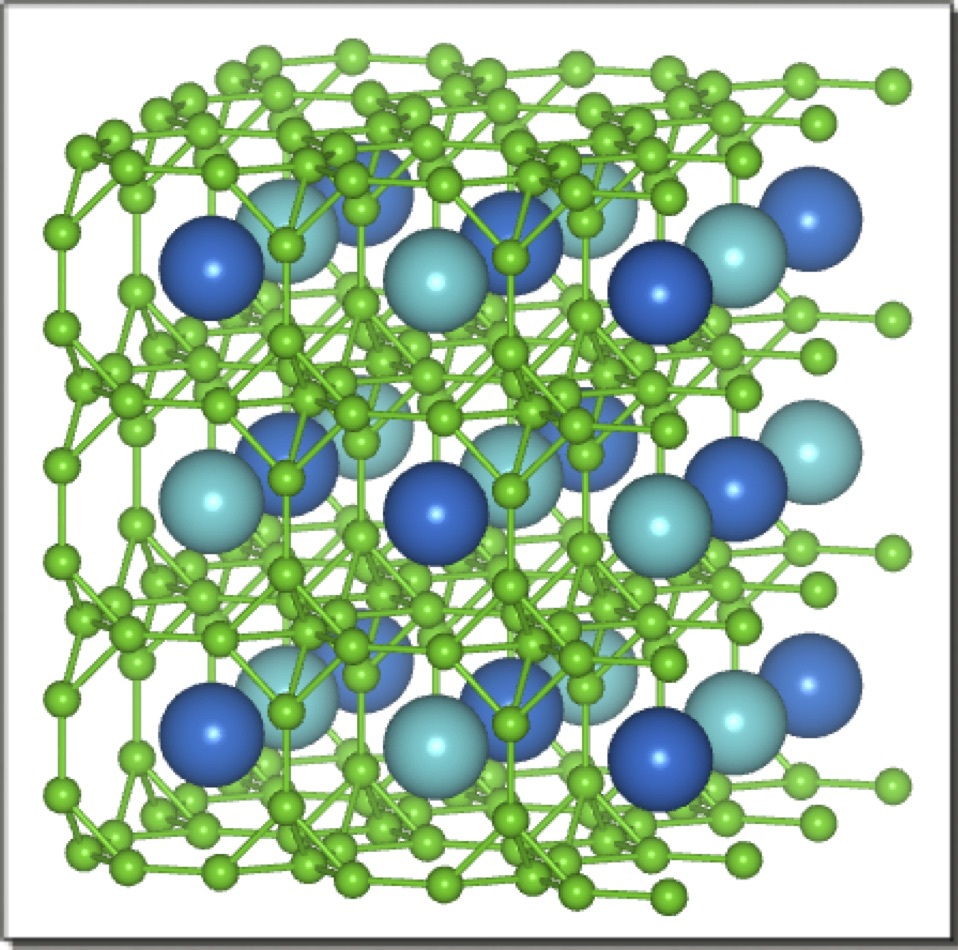
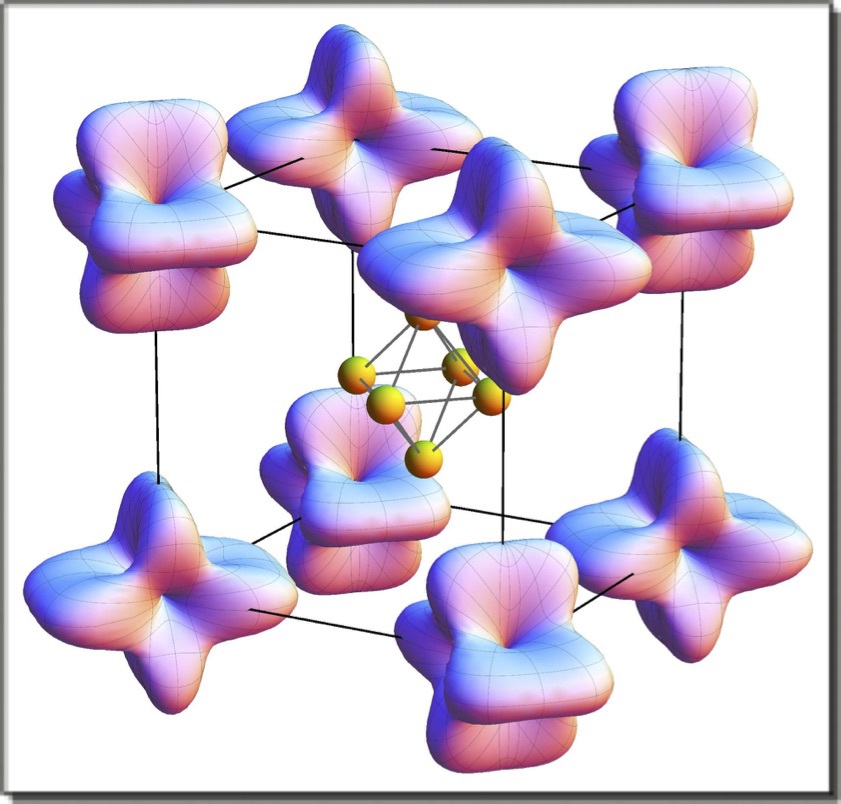
【2】AFQ相(II相)でのCeB6の構造． +Qの四極子をもつAサイト（青）と-Qの四極子をもつBサイト（水色）に分かれる． Para相(I相)ではすべてのCeは等価．

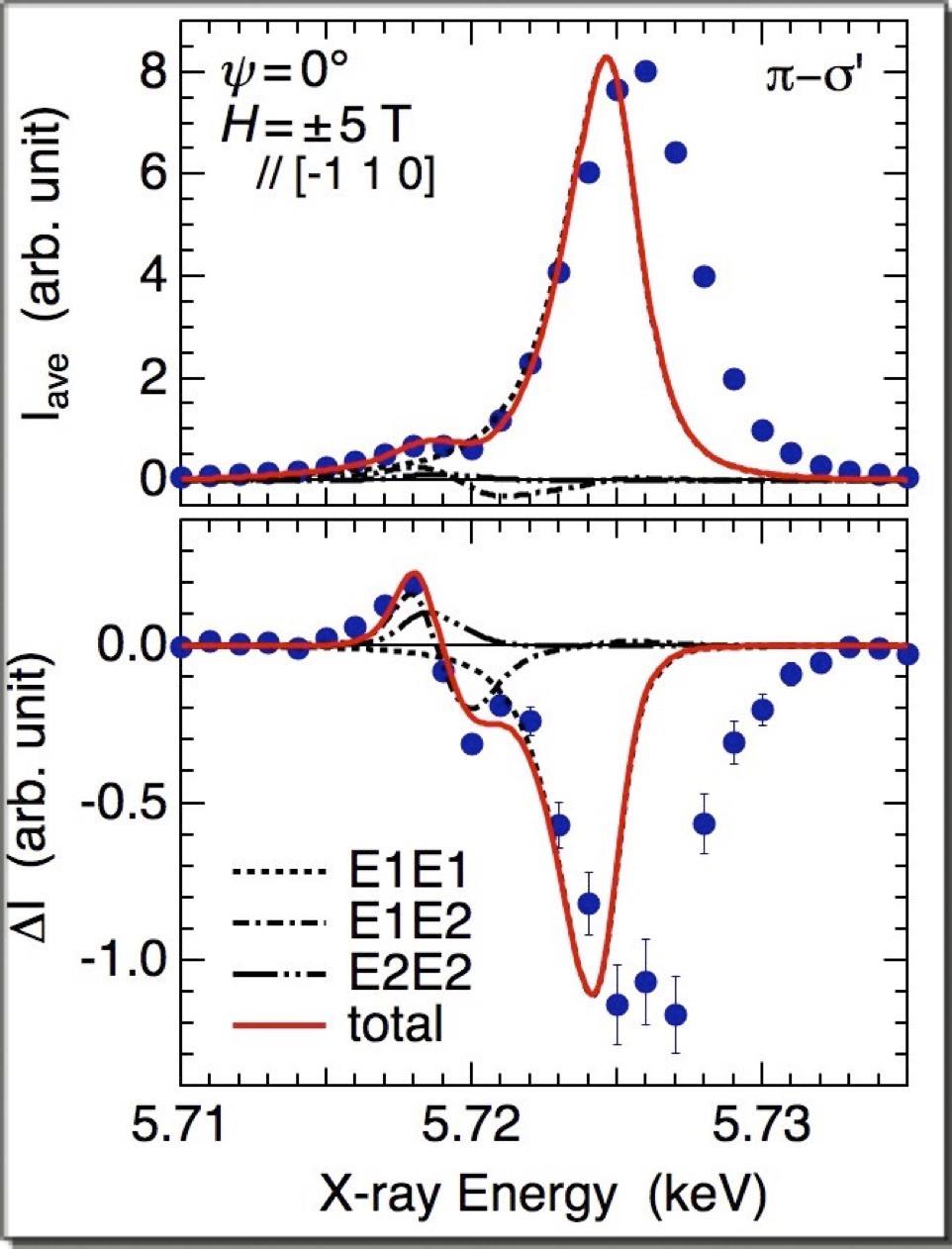
【5】バックグラウンドを差引き，吸収補正を行った±5 Tのデータ．スペクトルの平均(I+ + I–)/2と差分(I+ – I–)/2．比較曲線は計算．E1の平均は電気四極子，E1の差分は磁気双極子と電気四極子の干渉，E2の差分は電気四極子と磁気八極子の干渉からきていると解釈（PRB論文のFig. 8）．

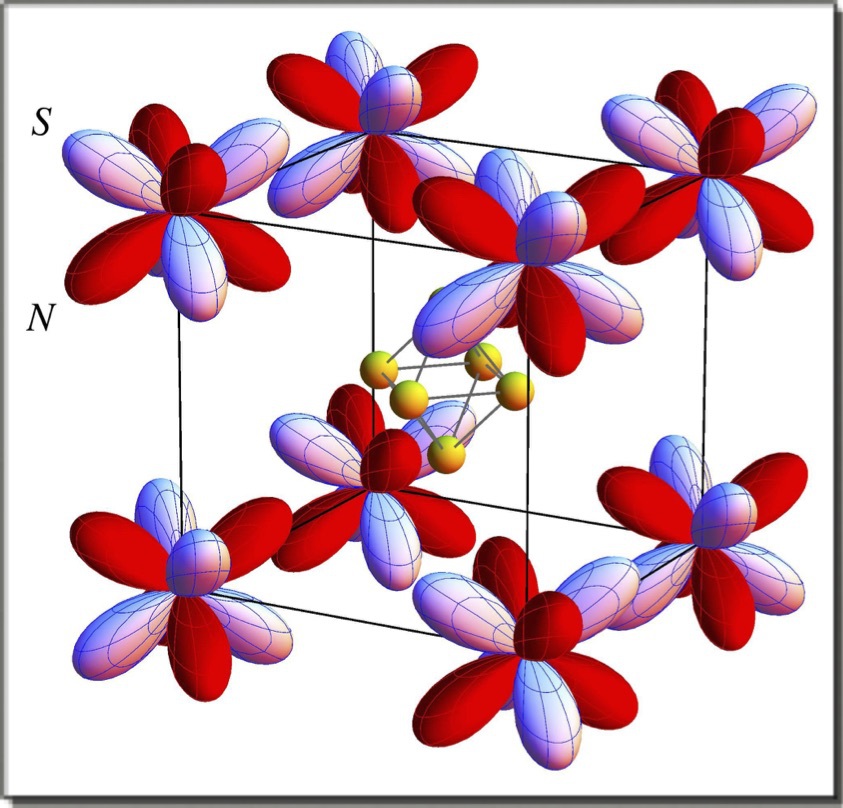
【3】AFQ相でのCeB6の4f電子電荷密度．Oxy型秩序を仮定しての計算．ここで，[001]方向に磁場をかけると，Txyz型磁気八極子が誘起される．

【6】CeB6のAFQ相で[001]方向に磁場をかけたときに誘起されるTxyz型磁気八極子．電荷密度が濃いところは上向きのNS．磁場方向が変わると，CeB6ではAFQ秩序変数が連続変化するので，どの磁場方向でもTxyz八極子が誘起される．

　立方晶化合物CeB6は1970年代から高濃度近藤効果を示す物質として研究対象とされてきたが，反強的電気四極子秩序 (AntiFerroQuadrupole order, AFQ) (TQ=3.3 K, TN=2.3 K) を示す典型物質としても非常に有名である．40年以上も研究対象とされ，高濃度近藤効果，重い電子，電気四極子秩序，磁気八極子秩序等，数々の新概念を創出し続けてきた驚くべき物質である． このような由緒ある物質の研究の歴史において，末席に名を連ねることができたことは望外の喜びといってよい．

◎ 研究背景

　歴史的にPara相をI相，AFQ相をII相，反強磁性磁気秩序相 (AntiFerroMagnetic order, AFM) をIII相と呼んできた．2.3 Kの反強磁性転移が鋭い比熱のピークを示すのに対して，3.3 Kでの比熱の異常は弱く，1970年代当初は不純物と考えられたこともあったが，磁場をかけると3.3 Kの転移温度が上昇し，比熱異常も大きくなっていくことが見出され，何か本質的な異常相が現れているにちがいないと考えられるようになった[1]．磁場をかけると非常に奇妙な反強磁性が誘起されてくることがNMRからわかり[2]，f電子系における反強的軌道秩序の理論[3]，中性子回折による磁場誘起反強磁性の観測を経て[4]，反強的電気四極子秩序(AFQ)の考え方が浸透していったのである．しかし，最大の矛盾はNMRから導き出された磁場誘起反強磁性の磁気構造と中性子回折が示すそれとが違うことにあった．NMRは直接磁気構造を観測するわけではないが，提案された磁気構造モデルと実験データとの整合性はよい．一方，中性子回折は直接磁気構造を観測するものであり，q=(1/2,1/2,1/2)の秩序，H//[001]のとき反強磁性は誘起されない，H//[110]のとき[001]方向の反強磁性が誘起される，といった実験結果は明瞭である．NMRの結果をどう考えたらよいかというのが，残された問題であった．

　このCeB6における最大の問題について，一気に矛盾のない解釈を導いたのが磁気八極子である[5]．上図【3】のようなAFQ秩序がある状況で[001]方向の磁場をかけると，AサイトでもBサイトでも [001]方向の磁気双極子が同じ大きさで誘起される．反強磁性はでてこないが， AFQ秩序が背景にあるので， AサイトとBサイトで[001]方向の磁気双極子Jzの分布が異なるはずだ．つまり，電荷密度が濃いところではJzの密度も濃く，薄いところではJzの密度も薄い．この球対称な磁気モーメント密度からのずれを多重極展開で表したものが磁気八極子であり，上図【6】のようなN極S極の分布で表すことができる．AサイトとBサイトで逆符号になっており，AntiFerroOctupole-order(AFO)である．この八極子は全対称表現Γ1に属する型であり，通称Txyz型と呼ばれる．他に，Γ4uタイプのTα（3成分）， Γ5uタイプのTβ（3成分）があり，計7成分の磁気八極子がある．このような磁気八極子を考慮してBoronサイトへのhyperfine fieldを計算すると，中性子と矛盾しない q=(1/2,1/2,1/2)の秩序からちゃんとNMRの結果が説明できることが示された[5,6]． Multipole (多極子)という概念が広く浸透していったのも，これがきっかけである．

　私達は磁気モーメントのことをふつうは一対のN極S極で表される磁気双極子だと考え，一本の矢印で表現する．しかし，実際に磁気モーメントを形成する電子は何らかの異方性をもった軌道状態をとっており，結果的に磁気モーメント密度も球対称ではなく，場所によって密度が異なる異方的なものになっている．それを表す物理量が磁気八極子である．大学院で青葉山の研究室に入ったとき，当時の科研にあった超音波の研究室とかかわりがあり，「弾性定数のソフト化が電子系の四重極応答を表す」という考えに出会った．弾性定数という，学生実験でやったヤング率みたいな古典的な物理量が，電子系のQuadrupoleというQuantum Mechanicalな量と結びつく．Quadrupoleという言葉の響きもcoolで，磁気モーメントといえば磁気双極子でしかなかった私はそのfantasticな概念に魅了された．博士論文のテーマにもなった．そして今度は ”Magnetic octupole” である．そのcoolな響きに魅了されると同時に，そんなものが現実に現れるとはなんということかと大きな衝撃を受けた．

　1990年代末までに磁気八極子まで登場したのだが，実はAFQ秩序もまだ直接の証拠として観測されたわけではなかった．中性子回折で観測されている磁場誘起反強磁性秩序を説明するためには，背後にAFQがなければならないというのがそれまでの最大の根拠である．やはり，中性子回折が磁気秩序を観測するように，Quadrupole momentが規則正しく周期構造を作っている様子を回折法 (diffraction) でダイレクトに観測しなければならない．中性子は電荷とは相互作用しないので，中性子によるAFQの直接観測は不可能である．そこで期待がもてるのはX線回折である．電磁波なので電荷と相互作用する．ただ，CeB6の全88個の電子のうち，AFQに関与するのはf電子たった1個であるから，普通のX線回折（Thomson散乱）で信号をとらえるのは厳しいかもしれない．でも，共鳴散乱を使えば強度の増大が期待できる．ちょうと1990年代末という時期は，d電子系で軌道秩序の観測に共鳴X線回折が有効であることが見出されたり，f電子系ではDyB2C2におけるAFQ秩序の観測(TQ=25 K)に共鳴X線回折が成功したりと，共鳴X線が日の出の勢いで世に出始めた頃であった[7,8]．しかし，転移温度3.3 K以下でX線回折実験をすることは当時は困難であった．液体ヘリウムが必要になってくるため，低温装置が大がかりになり，試料を自在に傾けることを目的とした4軸回折計とは相容れない部分があったのである．それでも，大変な労力を伴う作業を乗り越えて実験が行われ，見事観測に成功し，磁場による転移温度の上昇と散乱強度の増大（四極子秩序の磁場による増強）まで観測された[9]．ちなみに，CeB6のAFQは非共鳴のThomson散乱でも観測がなされている（論文の参考文献を参照）．

　その後，2005年になってKEK-PFにX線回折用8T縦磁場超伝導マグネットと，それを搭載する回折計(χ<±3°)が各種外部資金で導入され，1.7 Kまでの低温磁場中でX線回折実験が行えるようになった．温度領域が低温まで広がった上，磁場という新しい外部変数軸が導入されたことは大きい．CeB6が研究対象に入ってくる．当初，BL16に設置されていたころは作業も大変であったが，新ビームラインBL-3Aに移動してからは作業も効率化し，楽ではないにせよ，比較的気軽に実験ができるようになった．個人的には，こういうことが研究成果と大きく関わっているように思う．世界最高磁場や超低温など，性能ナンバーワンの突出した装置を導入することも重要である．しかし，その運転に多大な労力と資金を投入する必要があるのであれば，そう気軽に実験するわけにはいかず，運用回数が少なければ結果的に成果はでにくくなる．逆に，性能は最高でなくても，効率的な運転が可能で，気軽に実験できるのであれば，数多くの様々な実験がなされ，結果的に成果も多くなる．物性研究は多様性の世界であるから，たくさんの実験が気軽にできることは重要である．

◎ 我々の実験目的

　AFQの観測そのものはなされたので，次のステップに進まねばならない．CeB6のAFQ秩序変数はΓ_5g (Oxy)型（ゼロ磁場ではOyzとOzxとOxyの3ドメイン）であり，磁場中では3成分の線形結合で表され，磁場方向を方向余弦(α,β,γ)で表すとき，
　O_Γ=αOyz+βOzx+γOxy
が秩序変数になるとされている[6]．つまり，磁場方向を変えると秩序変数が磁場に応じて連続的に変化するというわけである．そう考えることでNMRや中性子回折の結果が説明できるというのだが，秩序変数であるからには何か一つに固定したものというイメージもあり，磁場でグニャグニャと変形するという概念自体かなり奇妙であると言わざるを得ない．これが本当にそうなのか，共鳴X線回折で直接観測して確かめねばならないというのが我々の実験目的であった．結果はたしかにそれを裏付けるものであったが，それは後に回すことにして，まずは思わぬ副産物として得られた磁場反転効果と磁場誘起磁気八極子の観測について述べよう． これらの実験と解析の過程では，共鳴X線のことも，多極子のことも，改めていろいろと学ぶことが多かった．

◎ 磁場反転効果

　磁場方向を変えたときにAFQ秩序変数が連続的に変化する様子を観測するため，KEK-PFのBL-3Aに設置された2軸回折計と8T縦磁場超伝導マグネットを用い，私と学生のTYとKKは，+4 Tの磁場中で試料(azimuthal angle, ψ)を回しながら(3/2, 3/2, 1/2)反射の共鳴スペクトルを測定していた（PRB論文のFig. 1の配置）．すると，H//[-110]のψ=0°でははっきり見えていた共鳴信号が，ψ=180°の H//[1-10] 付近になると非常に見えにくくなり，困ってしまった．試料は機械的に歯車で回しているので，回転させることでビーム中心からずれる可能性は否定できない．それによる強度変化は(3,3,1)基本反射の強度でモニターし，後で規格化するのがいつもの手段である．ところが，同じになるはずのψ=0°とψ=180°とが同じになりそうにないし，何か変だし，どうしたものかと困ったのである．それならば，試料を回さずに磁場方向を逆転させてチェックしてみようと思い，ψ=0°でマイナス磁場をかけてエネルギー依存性を測定してみた．すると，上図【4】の生データに示すとおり，磁場反転で異なるスペクトルが得られたのである．磁場反転しても試料が動いていないことは基本反射の強度で確認できているし， 理由はわからないけれど，これは何か本物をつかんだかもしれないと思った．ビームタイム中はとにかくデータだけとって，大学に帰ってから散乱振幅の式を基本からこねくり回し，磁場反転で一体自分たちは何を測定したのかを考えた．1ヶ月くらいかかってたどりついた結論が，E1とE2の干渉効果による磁場誘起磁気八極子の観測である．基本的な考え方はPRL論文に書いたが，きちんと整理した形で記したのはPRB論文である．

◎ 干渉効果

　磁場反転で強度が変わるのは異なる機構の散乱が重なることによる干渉効果である．要点だけ記すと，たとえばAとBの2種類の散乱機構があり，それぞれの構造因子をF_A, F_Bとすると，観測強度は|F_A+F_B|^2=|F_A|^2+|F_B|^2+(F_A^*F_B+F_AF_B^*)に比例し， (F_A^*F_B+F_AF_B^*)の部分が干渉項である． 強磁性の観測のように，Aが格子からの散乱でBが磁気散乱であるケースが典型例だが，今の場合はAがE1の磁気双極子(rank 1)でBがE1の電気四極子(rank 2)，AがE1の電気四極子(rank 2)でBがE2の磁気八極子(rank 3)のような，共鳴散乱項どうしでの干渉が主である．E1共鳴とE2共鳴は独立ではなく，エネルギーが近ければスペクトルが重なって干渉する．ちなみに，E1とE2のあいだの干渉効果に私が最初に出会ったのはDyB2C2である[10]．エネルギースペクトルをみると，E1とE2のあいだで鋭い極小がみられる．上図【4】の+Hでのスペクトルもそうである．E1とE2とが干渉せず，ただの足し合わせの強度|F_A|^2+|F_B|^2になるなら，このようなスペクトルにはならないだろう．DyB2C2での経験があったので，ここでも何かが干渉しているという直感が働いた．
　　
　PRL論文ではスペクトル関数を単純なものに仮定して解析した．より正しく定式化された理論で考察したのがPRB論文であり，その基礎となったのが長尾・五十嵐の論文である[11]．長尾・五十嵐による定式化で非常に重要なポイントは，異なるrankの多極子による散乱は異なるエネルギースペクトルをもつという点である．rank-νの多極子について，その幾何学因子からなる構造因子を，E1とE2に対してそれぞれZ_E1^(ν)およびZ_E2^(ν)と書くとき（PRB論文のAppendixを参照），全体の構造因子は
　F (ω) = α_E1⁽¹⁾(ω)Z_E1⁽¹⁾+α_E1⁽²⁾(ω)Z_E1⁽²⁾+α_E2⁽¹⁾(ω)Z_E2⁽¹⁾+αE_E2⁽²⁾(ω)Z_E2⁽²⁾+α_E2⁽³⁾(ω)Z_E2⁽³⁾+α_E2⁽⁴⁾(ω)Z_E2⁽⁴⁾
と表される．rankごとに異なるスペクトル関数で書くのが正しい書き表し方であり，エネルギー依存性を共通化した
　F (ω) = α_E1(ω){Z_E1⁽¹⁾+Z_E1⁽²⁾}+α_E2(ω){Z_E2⁽¹⁾+Z_E2⁽²⁾+Z_E2⁽³⁾+Z_E2⁽⁴⁾}
は，一見問題なさそうには見えるが，正しくない表し方なのである．スペクトル関数α^(ν)(ω)が重要なのである．

◎ 多極子秩序変数の磁場依存性

　上図【5】のように，強度の平均と差分をとり，構造モデルをたてて解析すると，いくつか仮定は持ち込まなければならないにせよ，それなりにもっともらしく各種秩序変数を分離して抽出することができる．H//[-110]での構造モデルは，Oyz-OzxのAFQ，Txyz-AFO，そしてJz-AFMが同時に発生しているというものである．ただし，AFQ相なので，磁気的にはparaであり，磁場を反転させるとTxyzとJzは符号を変えるがOyz-Ozxは符号を変えない．このモデルのもとで3つの秩序変数を抽出して，その磁場依存性をプロットしたのが下図【7】（PRB論文のFig. 10）である．Jzの磁場依存性は中性子とNMRの結果がすでに存在していたが，この図は電気四極子Oyz-Ozxと磁気八極子Txyzという，いわば隠れた秩序変数と呼ばれるものの磁場依存性を共鳴X線回折法で直接観測して得られたものと言ってよく，本論文をもっとも象徴する重要な結果だと思っている．

◎ 磁気八極子相互作用の存在

　ただ「磁気八極子を観測しました」というだけでなく，その磁場依存性まで測定したことで，Ceイオン間に磁気八極子相互作用が働いていることが言える．上で簡単に説明した考え方では，Oxy型AFQがある状況で磁場をかけると必然的にTxyz型八極子が誘起されるわけだから，Ceイオン間に磁気八極子を反強的に揃えようという相互作用がなくてもTxyzは誘起される．しかし，その場合，下図【8】のように<Txyz>と<Oyz-Ozx>の比を一様磁化Mに対してプロットすると，Mに比例した直線になるはずである[12]．ところが実験では上に凸の曲線になっている．これがCeイオン間に磁気八極子相互作用が働いていることを反映した結果である[12]．この図は非常に重要である．なぜなら，上図【1】のような右上がりの磁気相図が得られる理由の一つとして，これまで磁気八極子相互作用の存在が重視されていたのだが，その実験的証拠が得られたという大きな意義があるからである．

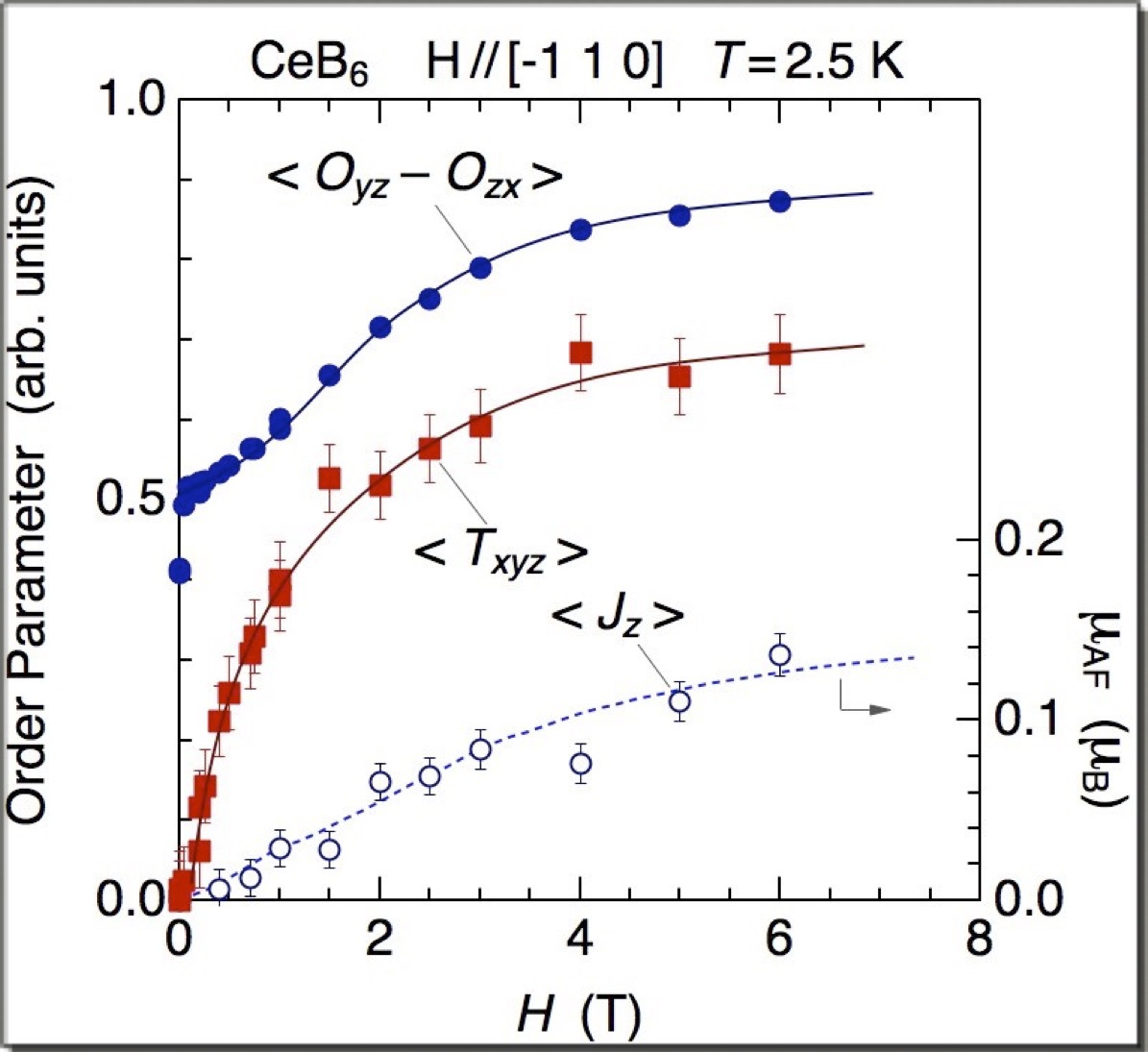
【7】CeB6のAFQ相，H//[-110]における秩序変数（電気四極子Oyz-Ozx，磁気双極子Jz，磁気八極子Txyz）の磁場依存性（PRB論文のFig. 10）．双極子の絶対値はNMRによるもの．

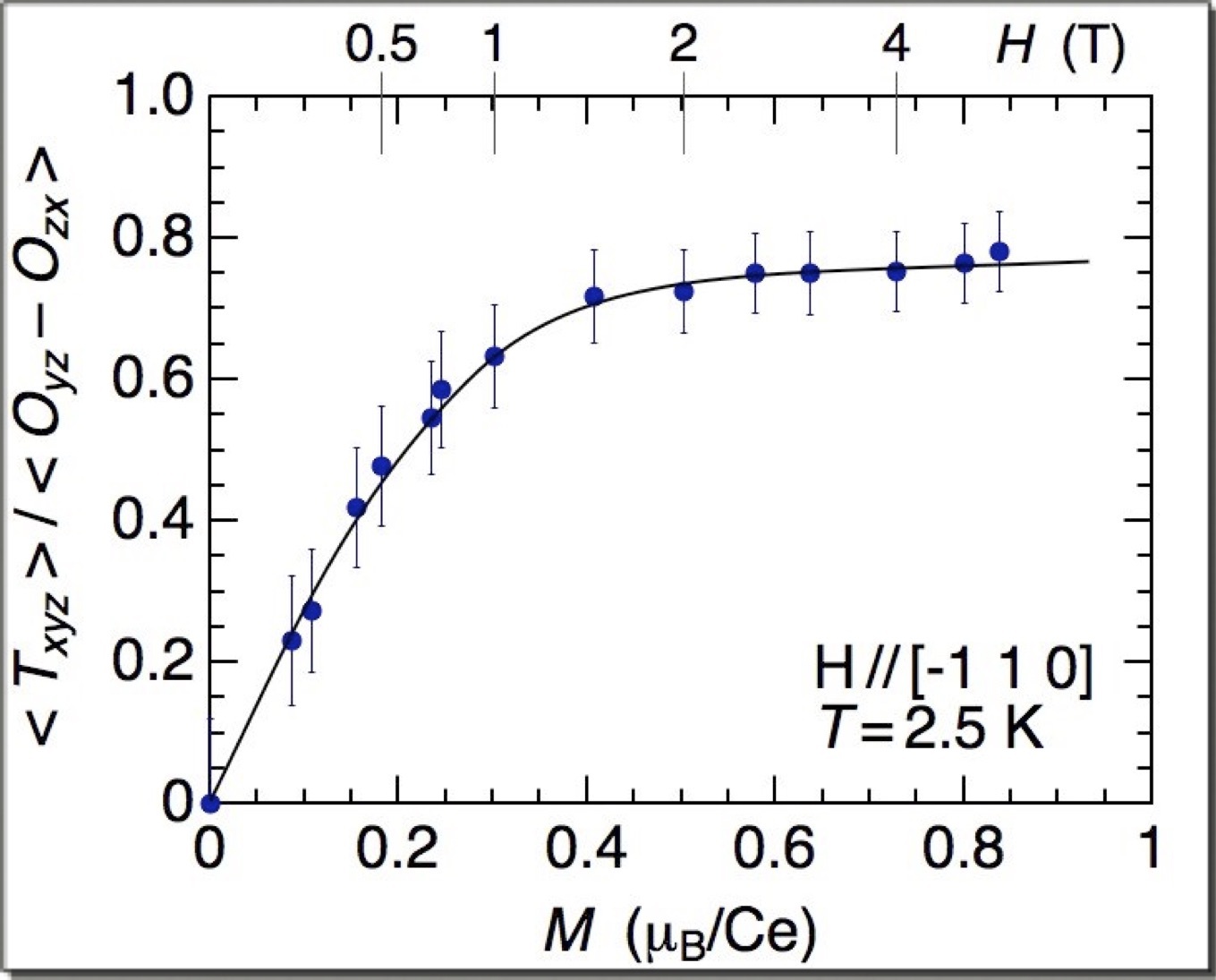
【8】<Txyz>と<Oyz-Ozx>の比を一様磁化Mに対してプロットしたもの（PRB論文のFig. 15）．Ceイオン間でTxyzの相互作用があると，このように上に凸の曲線になるが，なければMに比例した直線になるはず．

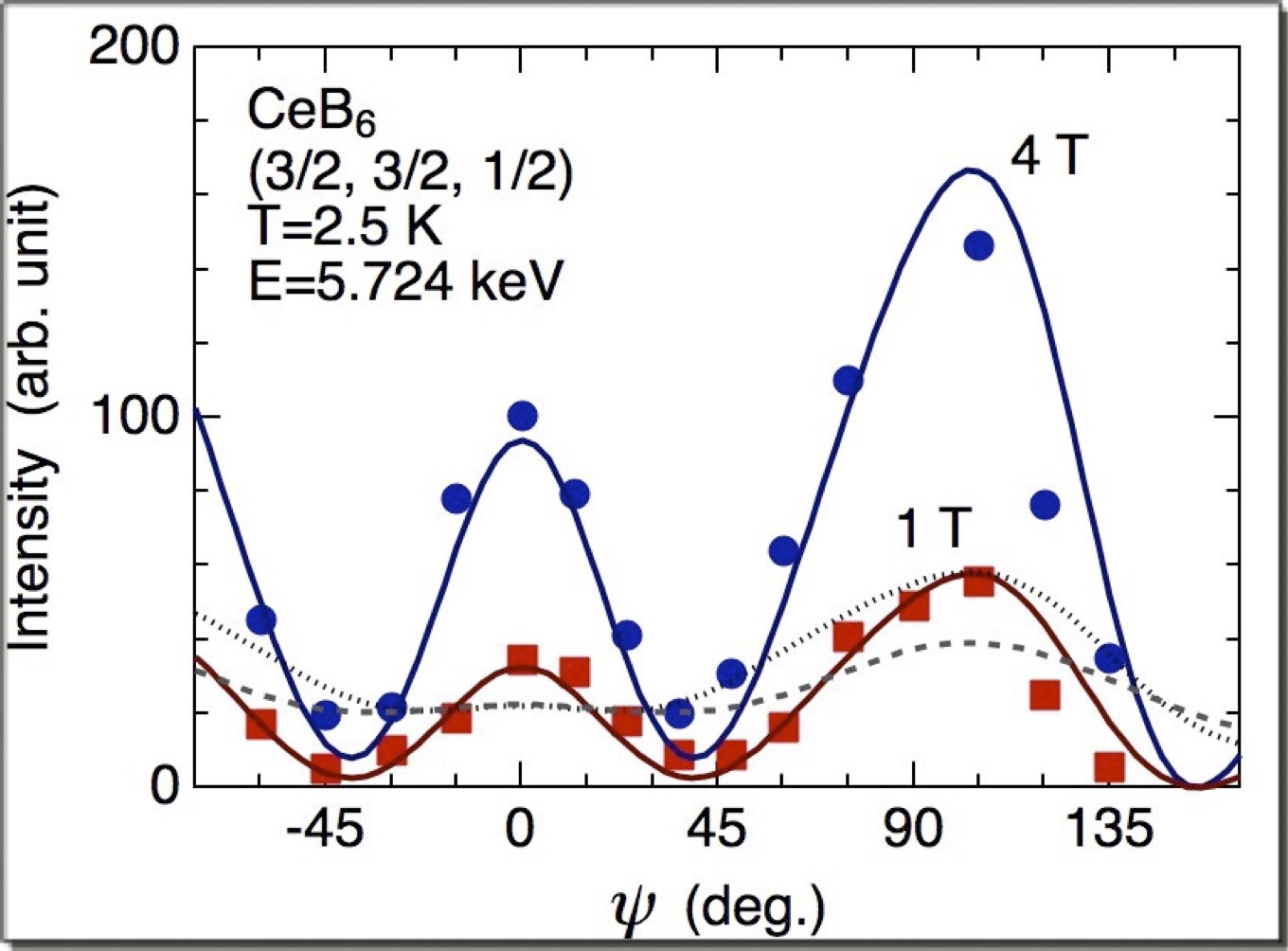
　当初の実験目的でもある「磁場方向に応じて連続変化するAFQ秩序変数」の測定結果が下図【9】である．もし本当にAFQ秩序変数が O_Γ=αOyz+βOzx+γOxy のような線形結合で表されているのなら，Oyz, Ozx, Oxyに対する構造因子をそれぞれFyz, Fzx, Fxyとすると，観測強度は|αFyz+βFzx+γFxy|^2に比例する．その場合の計算結果が実線である．実験データをよく再現している．一方，もしAFQ秩序変数がOyzとOzxとOxyにはっきり分かれており，3つの均等なドメインに分かれているならば，観測強度は|Fyz|^2+|Fzx|^2+|Fxy|^2に比例し，破線のようになる．また，磁場方向に応じてドメインが選択され，H//[001]ならOxy，[111]なら均等な3ドメイン，[110]ならOyzとOzxのようになるなら，観測強度は|αFyz|^2+|βFzx|^2+|γFxy|^2に比例し，点線のようになる．いずれも実験結果を説明できず，やはり線形結合と考えることで実験結果が最もよく説明できる．AFQ秩序変数が O_Γ=αOyz+βOzx+γOxy のような線形結合で表され，磁場方向に応じて連続的にグニャグニャと変形する様子を図示すると，下図【10】のようになる．

【9】+4 Tと+1 Tの磁場中で散乱ベクトル(3/2, 3/2, 1/2)を固定したまま試料を回転（磁場方向を回転）し，強度変化を測定した結果（PRB論文のFig. 2）．

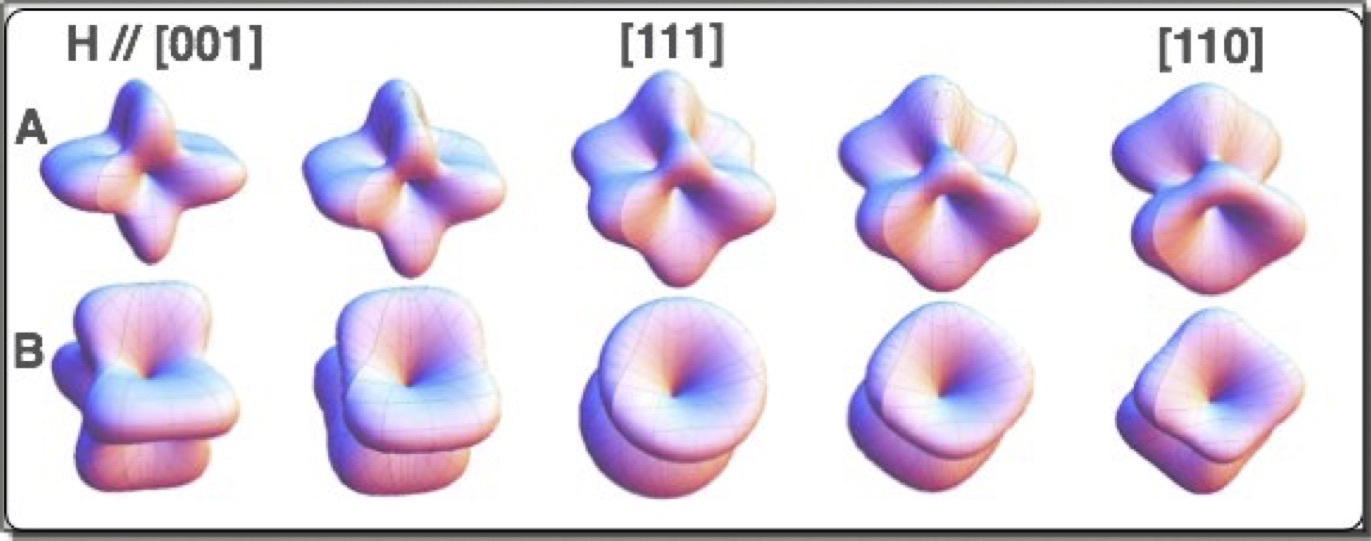
【10】H//[001]からH//[111]を通ってH//[110]に至るまでのAFQ秩序の変化の様子（計算）．H//[001]ではOxy，[111]ではOyz+Ozx+Oxy，[110]ではOyz+Ozx．その間をグニャグニャと連続的に変化する．

[1] T. Fujita et. al., Solid State Commun. 35, 569 (1980).
[2] M. Takigawa et. al., J. Phys. Soc. Jpn. 52, 728 (1983).
[3] F. Ohkawa, J. Phys. Soc. Jpn. 52, 3897 (1983); 54, 3909 (1985).
[4] J. M. Effantin et. al., J. Magn. Magn. Mater. 47&48, 145 (1985).
[5] O. Sakai et. al., J. Phys. Soc. Jpn. 66, 3005 (1997).
[6] R. Shiina, J. Phys. Soc. Jpn. 66, 1741 (1997); 67, 941 (1998).
[7] Y. Murakami et. al., Phys. Rev. Lett. 80, 1932 (1998); 81, 582 (1998).
[8] K. Hirota et. al., Phys. Rev. Lett. 84, 2706 (2000).
[9] H. Nakao et. al., J. Phys. Soc. Jpn. 70, 1857 (2001).
[10] T. Matsumura et. al., Phys. Rev. B 71, 012405 (2005).
[11] T. Nagao and J. I. Igarashi, Phys. Rev. B 82, 024402 (2010).
[12] R. Shiina, J. Phys. Soc. Jpn. 70, 2746 (2001).