磁場と電荷とはふつうはエネルギー的に結合しないはずなのに， 磁場誘起電荷秩序というのは非常に奇妙なタイトルである．このような秩序が形成されるとは全くの驚きである．かつてない新奇性であり，新種の秩序状態を見出したといっても過言ではなかろう．もちろん，スピンが介在して磁場と電荷とをつなぐ役割を果たしているのであって，磁場と電荷が直接相互作用しているわけではないが，この機構が実に巧妙なのである．磁場を反転させると原子変位も反転したり，磁場と平行な反強磁性が誘起されたりといった奇妙な現象が起こる（ふつう，反強磁性モーメントは磁場と垂直な方向を向く）．

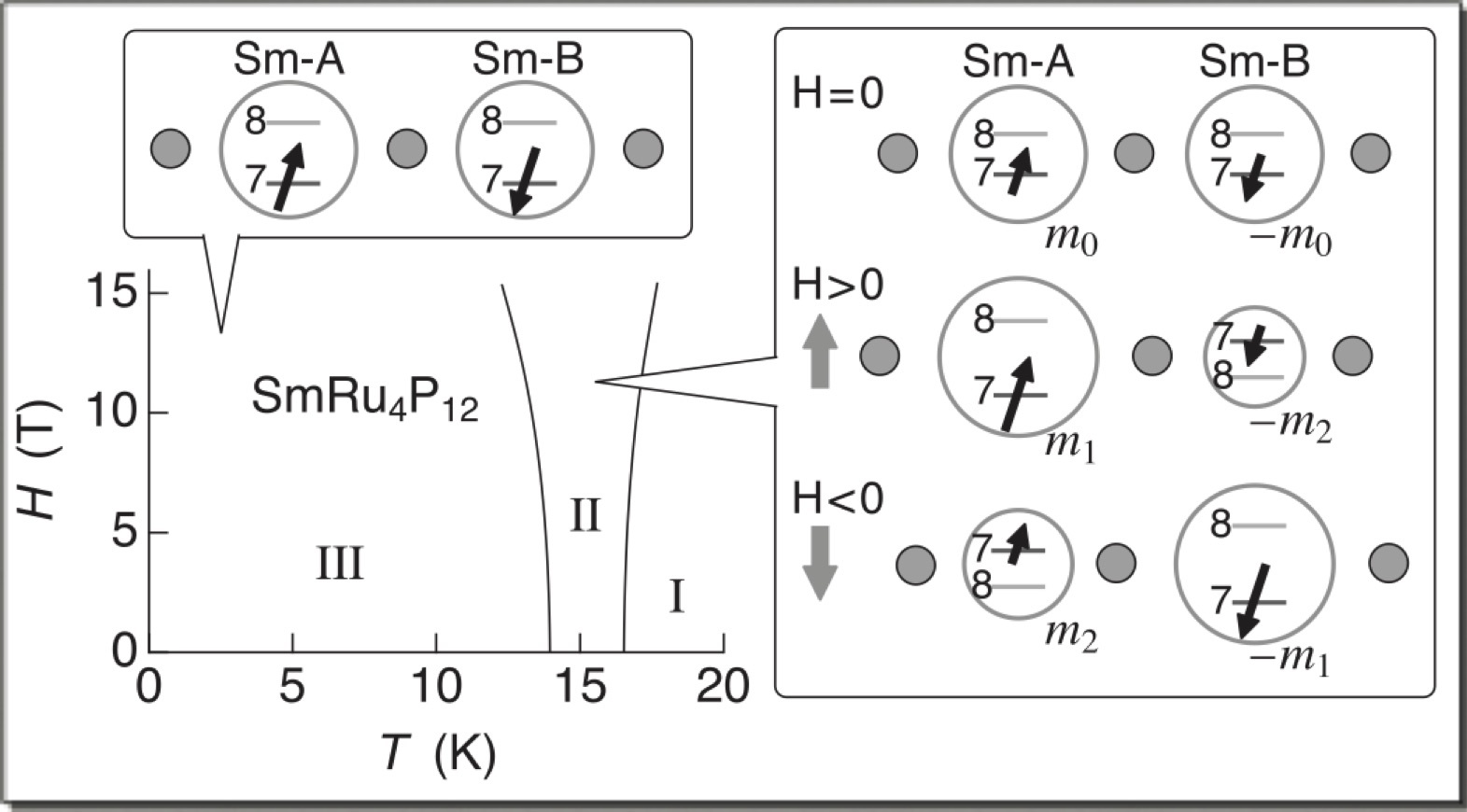
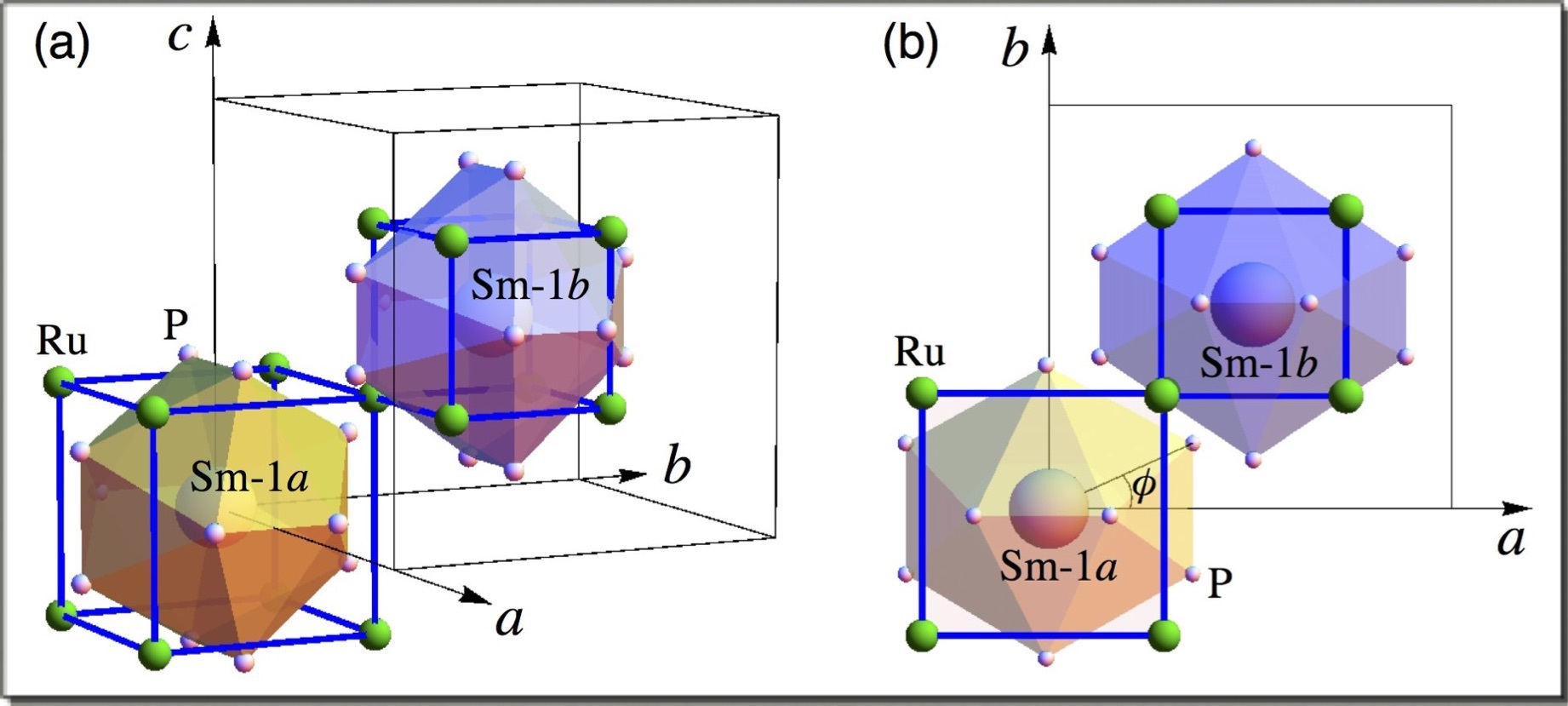
【1】SmRu4P12の磁気相図と磁場誘起電荷秩序の模式図．Smサイトの大きな丸はP12分子軌道のp電子密度，小さな丸は周囲の原子を表す．磁場を反転させると電荷密度の濃淡，Smサイトの結晶場準位，原子変位が反転する．（論文のFig. 1）

【2】SmRu4P12の結晶構造．

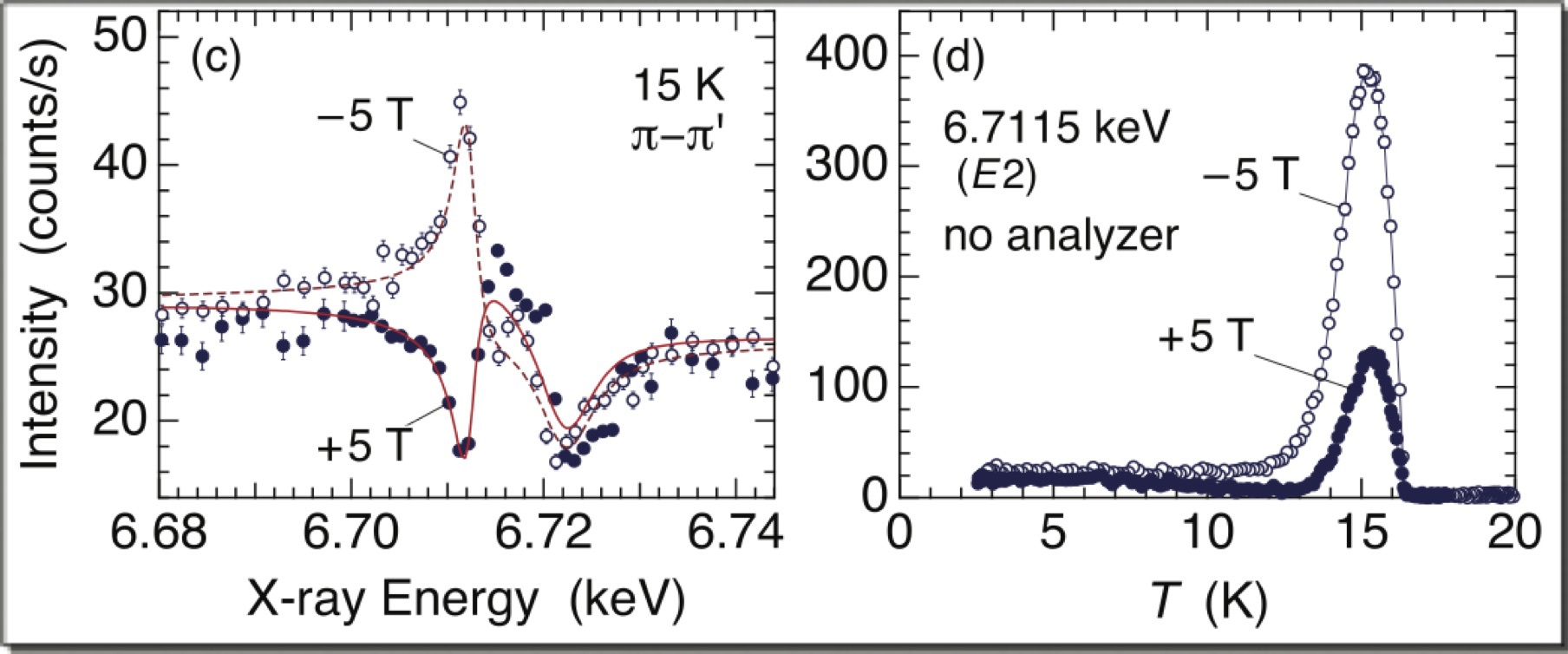
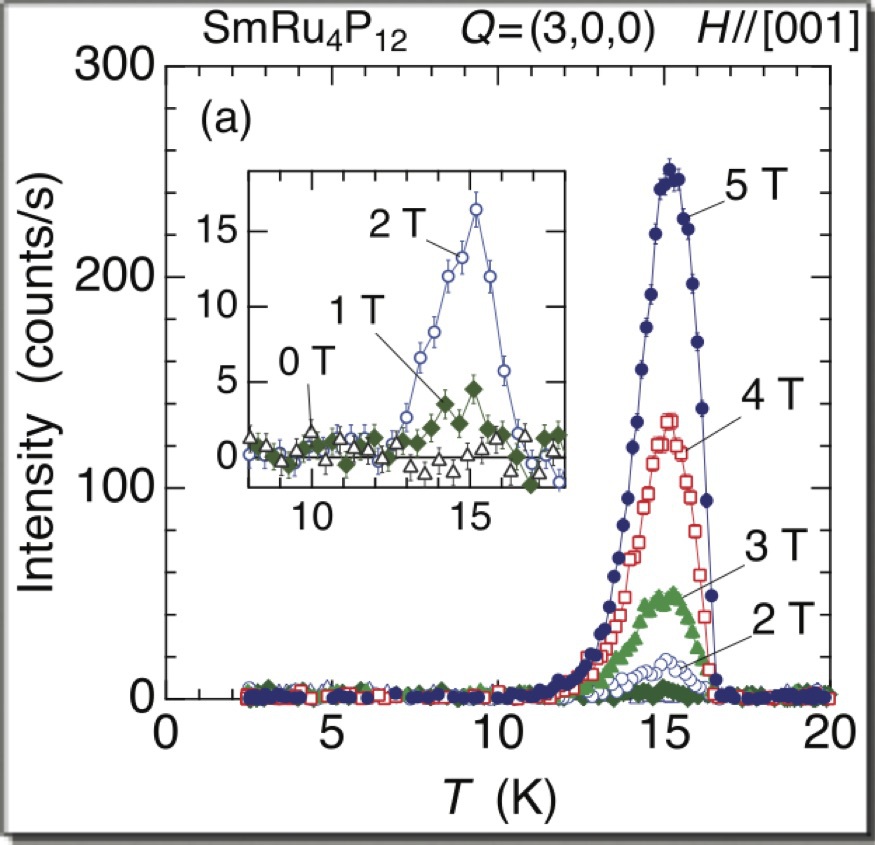
【3】(c) 中間相15 K，磁場±5T//[001]における(3,0,0)反射強度(π-π’)のエネルギー依存性．実線は計算．(d) E=6.7115 keVでの強度の温度依存性．反強磁性による磁気散乱と原子変位によるThomson散乱との干渉で磁場反転効果が現れる．

【4】E=6.68 keV（非共鳴）における(3, 0, 0)反射強度の温度依存性．磁場を[001]方向にかけている．

◎ 研究背景

スクッテルダイト化合物の一つであるSmRu4P12はT_MI=16.5 Kで金属絶縁体転移を起こすと同時に磁気的な秩序状態に転移することが知られていた [1]．しかし，その秩序相内に別の転移 (T*≈14 K) が存在し，磁場印加と共にT*での比熱等の異常が増強されていく現象がみられ，この中間相(T* < T <TMI)の正体が長年の謎であった [2]．磁気八極子秩序ではないかとの論考もあったが，決定的な結論には達しなかった．そのような状況の中，最近，椎名により，p-f混成を起源とする CDW不安定性に基づく解釈が提案された [3]．多極子とは異なる切り口からの解釈であり，興味を抱いた私達はこれを検証するため，SPring-8のBL22に設置した超伝導マグネットを用いて磁場中共鳴X線回折実験を行った（Ce0.7La0.3B6の論文解説参照）．
　その結果，T* < T <T_MI の中間相において，磁場によって誘起される共鳴散乱信号を観測することに成功した．同時に，原子変位による非共鳴散乱も磁場中で誘起されることもわかった．多極子による解釈よりも磁場誘起電荷秩序のシナリオのほうがずっと実験結果との整合性がよいと私達は考えている．

◎ p-f混成によって引き起こされるCDW

電荷秩序の理論の要点は，結晶場で分裂したSmのf電子軌道（Γ7かΓ8か）によって，伝導バンドを形成するP12分子軌道との混成が異なる点にある[3]．対称性により，Γ7のみが伝導を担うP12分子軌道と混成する．そのため，隣接するSm原子間での反強磁性相互作用はΓ7のあいだでのみ起こり，反強磁性秩序はΓ7状態で形成される．これがゼロ磁場での反強磁性であり，まったく普通の反強磁性秩序である．一方で，P12分子軌道は体心立方格子の特徴を反映して，波数ベクトル(1,0,0)で電荷密度波 (CDW) を形成する強い不安定性をもっている [4]．頂点位置のSmまわりと体心位置のSmまわりでp電子は電荷密度の濃淡を作りたがっているのである．実際，PrRu4P12では60 KでCDW転移が起こる．ただし，P12分子軌道のp電子だけでCDWを形成するには至らず，p-f混成を通じてf電子の自由度を利用する必要があるところが面白い．SmRu4P12の場合，ゼロ磁場の反強磁性秩序相では頂点Smも体心SmもΓ7状態であり，CDW形成は起こらない．しかし，磁場をかけるとZeeman分裂により，Γ8状態が混じってくる．これがp-f混成を通じて伝導バンドのCDW不安定性と結びつき，頂点と体心でΓ7とΓ8が交互に並んだ構造をとることでCDWを実現させ，エネルギーの低い状態をつくることになる．これが磁場誘起CDW（電荷秩序）である．Γ7とΓ8という結晶場状態の秩序ということでスカラー秩序(Scalar Order)とか，十六極子秩序(Hexadecapole Order)と呼ばれることもある．

◎ 磁場と平行な反強磁性

Γ7とΓ8が交互に並んだ秩序状態では，Γ7サイトとΓ8サイトで磁気モーメントの大きさが異なってくる（上図【1】，論文のFig. 1）．普通の反強磁性であれば，どのサイトの磁気モーメントも大きさが同じであろうとするので，磁気モーメントは磁場と垂直方向を向き，磁場方向にわずかにキャントすることでZeemanエネルギーを得しようとする．しかし，今の場合，Γ7サイトとΓ8サイトで磁気モーメントの大きさが異なっているので，磁場と垂直になるよりは，平行になったほうが全体としてZeemanエネルギーを得することができる．磁場と平行な磁気モーメントをもつサイトでは，Γ7が基底状態となって大きな磁気モーメントを作り，逆に磁場と反平行な磁気モーメントをもつサイトでは，Γ7が励起状態となって磁気モーメントが小さくなる．そのため，磁場と平行な反強磁性秩序が形成されることになる．磁場中共鳴X線回折で観測した中間相での強度増大（6.7115 keV, E2共鳴）は，まさにこの磁場と平行な反強磁性を観測していることが偏光解析からわかる（π-π’散乱，上図【3】）．実験では原子変位によるThomson散乱と干渉効果を起こし，磁場反転で強度が激変するという効果が見えている．これを利用することでより精度よく磁気散乱成分だけを抽出することができた（論文のFig. 3）．干渉効果の測定と解析では，CeB6やCe0.7La0.3B6での経験が生きている．

◎ 磁場誘起原子変位

磁場中で原子変位も誘起されることがわかった（上図【4】，論文のFig. 4）．π-π’散乱で非共鳴型の信号がおなじ波数ベクトルでの信号にのってくることから，原子変位を反映したThomson散乱であることがわかる．P12分子軌道での電荷秩序に伴って生じた原子変位であると考えられる．磁気散乱との干渉効果を解析すると，磁場を反転させると原子変位も反転することがわかった．

　原子変位の詳細を調べたのが次の論文IIである．磁場方向を変えたより詳しい共鳴X線回折実験の結果は，その次の論文で発表される予定である．


[1] C. H. Lee et al., JPSJ 81, 063702 (2012).
[2] K. Matsuhira et al., JPSJ 71, Suppl. 237 (2002).
[3] R. Shiina, JPSJ 82, 083713 (2013).
[4] H. Harima, J. Phys. Soc. Jpn. 77, Suppl. A 114 (2008).

◎ 磁場誘起原子変位が電荷秩序に対応した全対称型であること

論文Iで存在が明らかになったII相における磁場誘起原子変位を詳しく調べた．低温，磁場中という，技術的にも困難な状況で，格子基本反射の5桁~8桁落ちの弱い強度をできるだけ多く集めて結晶構造解析をするという，なかなか大変な実験である．測定できるのは水平散乱面内の十数点の反射点に限られ，しかも，ビームサイズに比べて大きな試料（論文Iと同じ試料）からの反射を測定するため，回折計の幾何学的配置による系統誤差も大きく， R因子を数%以下まで持っていくような本格的構造解析とは言えないが，それでも第0近似での構造は同定したと言えるくらいのデータだと考えている．詳しいデータは論文のFig. 1~3にあり，見た目はそれなりにきれいだ．
　解析の結果，磁場誘起電荷秩序相での結晶構造は，ゼロ磁場でのPrRu4P12と同様，単純立方の空間群Pm-3型であることがわかった（常磁性相では体心格子のIm-3）．Pm-3では，Ruの原子位置はSm-1aまわりで(1/4+d,1/4+d,1/4+d)，Sm-2aまわりで(1/4-d,1/4-d,1/4-d)，Pの原子位置はSm-1aまわりで(0,y+du,z+dv), Sm-2aまわりで(1/2,y-du,z-dv)と表され，Sm-1aまわりで膨張，Sm-1bまわりで収縮している（上図【5】，論文のFig. 4）．d, du, dvは磁場方向によって若干の変化はあるが，だいたい10^-4のオーダーである．PrRu4P12と同程度だ．
　空間群Pm-3というのは，立方晶の空間群であるから，磁場中での結晶構造を表す空間群としては，厳密にはもちろん正しくない．かけた磁場方向によって原子変位も微妙に違っているであろうから，本当は立方晶ではなくなっているはずである．しかし，その変化はIm-3からPm-3への変化と比べれば小さく，今回の実験で明瞭な強度差として検出できるほどのものではなかった．つまり，磁場中II相での結晶構造は，第0近似でPm-3型であると考えてよいだろう．また，次に述べるように，超精密構造解析からは，秩序相では菱面体(Rhombohedral)に歪んでいることがわかっている．これも超精密測定をしたから見えたことであって，この原子変位の測定では4つの菱面体ドメインからの反射をすべて同時に測定しており，立方晶にしか見えない．
　II相における上図【5】の構造は PrRu4P12と同様な構造であり，このことも SmRu4P12のII相が磁場誘起型の電荷秩序相(Charge Order, Scalar Order, Hexadecapole Order)であることを物語っている．

【5】II相磁場中での原子変位の模式図（実際の変位を誇張して描いてある）．Pm-3空間群を仮定している．Sm-1aまわりのRu立方体が膨張，Sm-1bまわりで収縮，それに呼応するようにP位置を決める角度φがSm-1aまわりで大きく，Sm-1bまわりで小さくなっている．（論文のFig. 4）

【6】実験時の試料部分の様子．(111)面と(100)面を出したSmRu4P12試料を直径8mmの台座上に貼り付けている．ビームサイズは1x1mm2であり，図中の正方形部分程度．

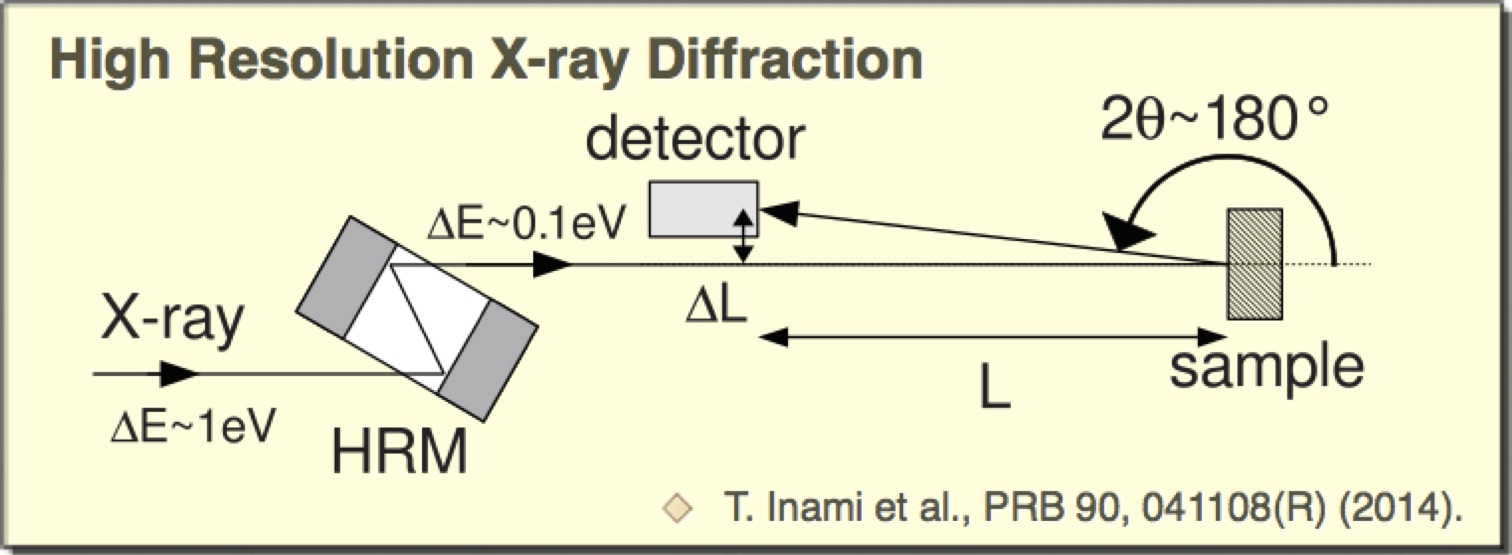
◎ 超精密格子定数測定

　共同研究者である稲見氏により手法開発された，超精密格子定数測定について述べよう．この手法はCexLa1-xB6の磁気八極子秩序の研究に適用された実績があり[ PRB 90, 041108 (2014) ]，現在では，BL22での測定オプションとなっている．共鳴散乱の実験からそのまま移行できるのも強みだ．

　X線回折による格子定数の精密精度は，λ=2dsinθの関係から，θを90°（2θを180°）に近づけるほど向上することは教科書にも載っており，よく知られている．さらに精度を上げるには，λ（=12.394/E，つまりエネルギー）の精度も上げる必要がある．そのため，ここで用いる手法では，放射光ビームラインのモノクロメータからでてくる，約1eVの幅をもったX線を，さらにシリコン単結晶 (High Resolution Monochrometer, HRM) で2回反射させ，約0.1eVの幅までしぼる ．これで精度が10倍向上する．残りの精度は結晶の品質（dの幅）で決まってくる．θの精度，X線エネルギー（1/波長）の精度，結晶の面間隔のばらつき，の3要素のconvolutionで測定精度が決まるのである．

【7】超精密格子定数測定の原理図（左）と，実際の測定時の様子（右）．検出器の横のわずかなすき間からビームを試料部へ導き，ほとんど180°（179.5°くらい）で反射して同じ管の中を通ってきたX線を検出器でとらえるという，ふつうは見ることのない特殊な実験配置となっている．

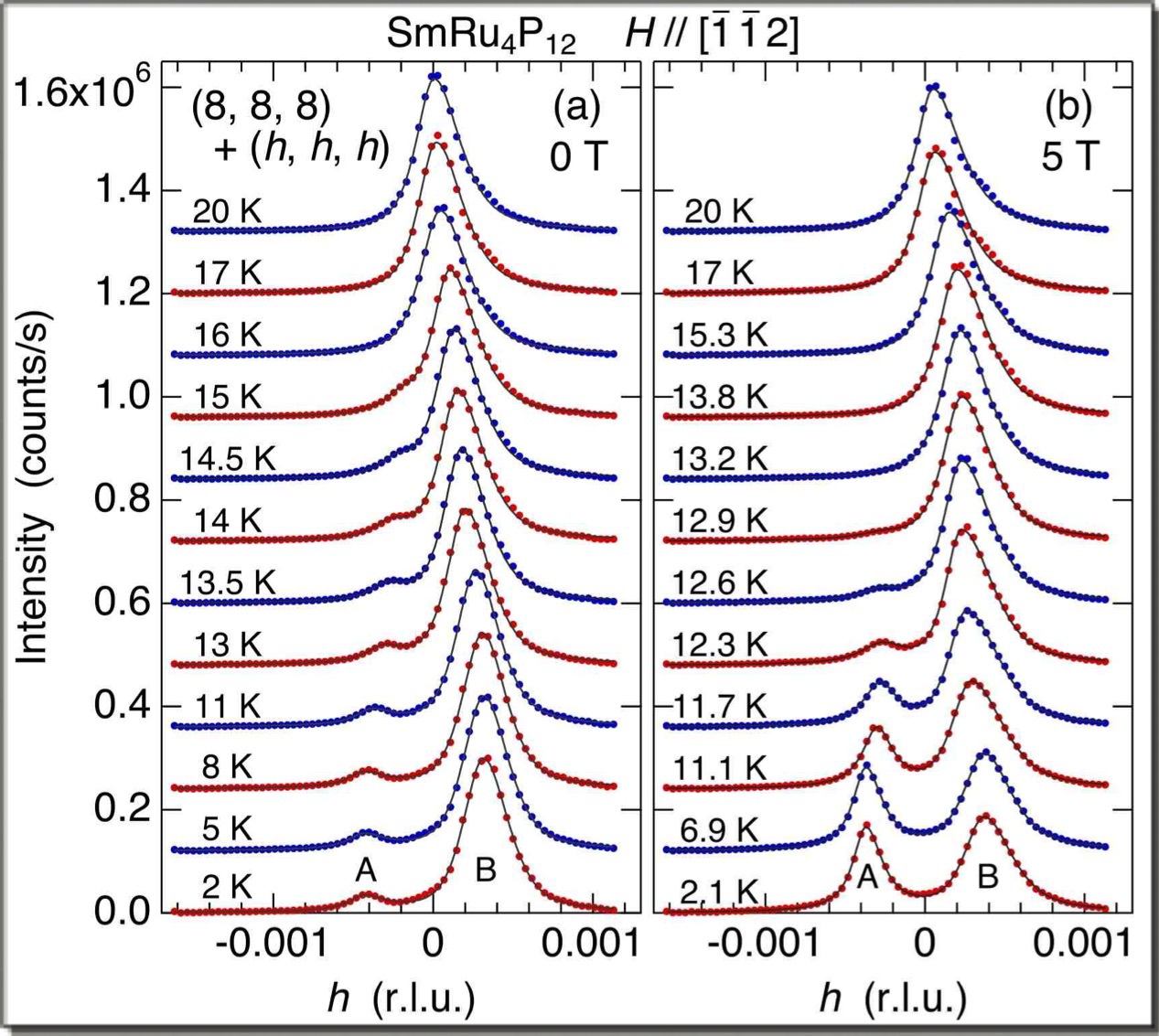
【8】(8,8,8)反射のピークプロファイルの温度変化．（論文のFig. 6）

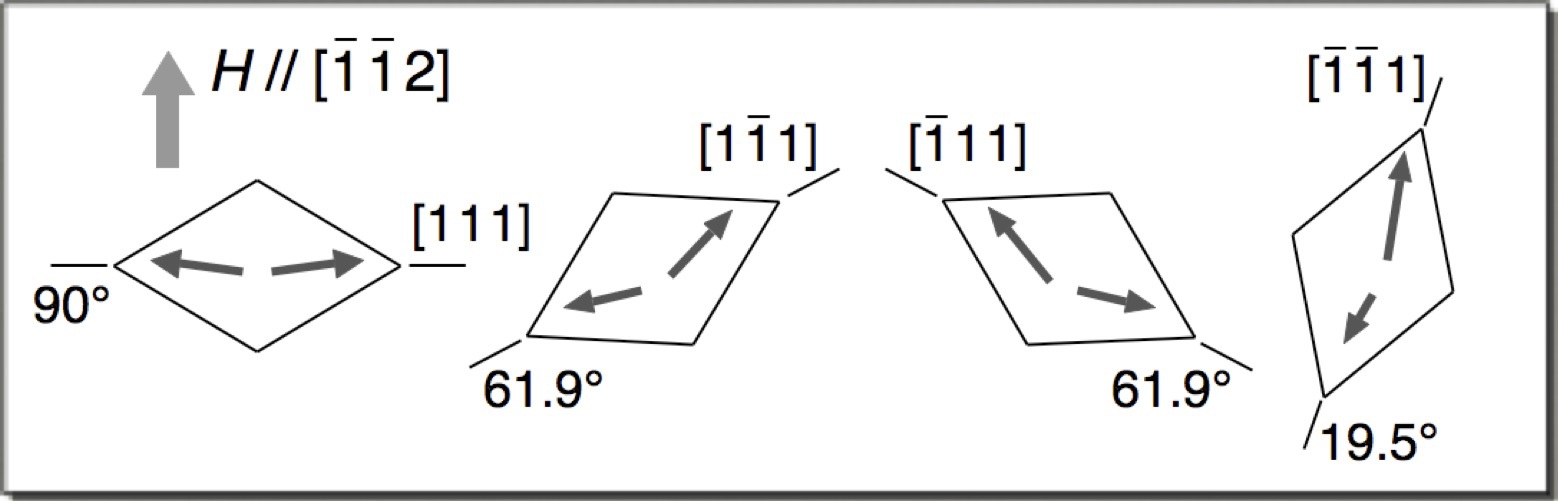
【9】H//[-1 -1 2]のときの4つの磁気ドメインの模式図．角度は磁場方向と菱面体の主軸方向とがなす角．（論文のFig. 11）

◎ 磁気秩序に伴う菱面体(Rhombohedral)歪みの観測

(8,8,8)反射のピークプロファイルを測定した結果を【8】に示す．この測定では，θを変化させるのではなく（θはほとんど180°に固定されている），X線のエネルギーを変化させている．ビームラインのモノクロメータは固定しておき，【7】の図のHRMを回転させることで，高い分解能でX線のエネルギーを変えている．図はエネルギーを逆格子空間の指数に焼き直して表示したものである．指数にして7.999から8.001までという，ふつうは見ることのない高精度の測定になっていることがわかるであろう．また，磁気秩序相に入るとピークが分裂しているのがよくわかる．これは(8,8,8)反射の面間隔が2種類生じたことを表しており，立方晶から菱面体へと変化したことを示している．HRMを入れずに，ふつうに測定すると，幅が10倍くらいに広がったデータになるので，全く分裂が見えないことは明白である．
　おもしろいのは，4つある菱面体ドメイン のうち（立方晶では等価な[1 1 1], [1 -1 1], [-1 1 1], [-1 -1 1]軸のどれかが伸びて菱面体になるので4つのドメインができる），中間相（II相）では1つしか見えない点である．【9】の図で[-1 -1 1]ドメイン（ピークB）だけが観測されて，[111]ドメイン（ピークA）は観測されない．これは，磁場と平行な反強磁性をもつドメインだけが選択されていることを示しており，共鳴散乱の結果とよく対応している．

◎ 残された課題

　低磁場極限でII-III相境界は存在するかという問題は未解決である．磁場中での伝導現象も，電荷秩序形成と金属絶縁体転移，バンド構造の変化の観点から今後研究すべき課題である．p-f混成強度は圧力によって変化するはずなので，圧力応答の研究も意義深い．原子変位は観測したが，p電子の濃淡そのものを観測したわけではないし，Γ7とΓ8の秩序も直接観測されたわけではない．なにより，モーメントの長短と電荷密度の濃淡の関係（位相関係）が，模式図ではわかったように描かれているが，想像図にすぎず，実はわかっていない．