1.Introduction ― What is Magneto-Science? ―
Please click here to see by a PDF version. >>>131104-Introduction
All substances consist of atoms. All atoms comprise electrons and nuclei. Because the spin and orbital motions of electrons produce magnetism, no substance is without magnetism. Therefore, it is reasonable to expect that chemical and physical behaviors of all substances are affected to some degree by a magnetic field. Magneto-science deals with the influence of magnetic fields on chemical, physical, and biological phenomena and the application of magnetic fields in industry.
The effects of static magnetic fields on chemical and physical processes have been discussed elsewhere in detail [1]. Those effects are divisible into three groups, as shown in Table 1. The first, quantum mechanical effects, arise from the interaction of electron spins in short-lived reaction intermediates called radical pairs. In photochemical reactions of organic molecules, radical pairs are generated as intermediates. Product yields and radical pair lifetimes are affected by an external magnetic field (MF). The second is thermodynamic effects. Crystals are often oriented in one direction when crystallization occurs in an MF. This orientation happens when a crystal is magnetically anisotropic. The third is mechanical effects, consist of three mechanisms. In electrochemical reactions, the transport of reactants in bulk solution to electrodes is a key process. The motion of ions and electrons in the solution is affected by Lorentz force. The magnetic force is well-known to be proportional to the product of magnetic flux density and its gradient. One application is magnetic levitation of diamagnetic materials. Magnetic susceptibility force, which is proportional to the product of the magnetic susceptibility gradient of solutes in solution and the square of magnetic flux density, is operative in crystal growth from solution. Examples of these effects will be presented.
Table 1 Classification of magnetic field effects
Type of effect | Type of MF | Mechanism | Example |
| Quantum mechanical effect | Homogeneous | Radical pair mechanism | Photochemical reaction |
| Thermodynamic effect | Homogeneous | Anisotropic magnetic energy | Magnetic orientation |
| Mechanical effect | Homogeneous | Lorentz force | Electrochemical reaction |
| Mechanical effect | Inhomogeneous | Magnetic force | Magnetic levitation Magnetically simulated microgravity |
| Mechanical effect | Homogeneous | Magnetic susceptibility force | Crystal growth |
1. Quantum Mechanical Effect – Radical Pair Mechanism

Therefore, the cage product and escape product yields are affected by an MF. To obtain a large magnetic field effect, a radical pair must have a sufficiently long lifetime so that hfi-induced spin transitions occur at a zero field. Micellar solutions are often used because a micelle provides an ideal cage for an organic radical pair dissolved in it.
Magnetic field effect (MFE) on photosensitized oxidation of 1,3-diphenylisobenzofuran (DPBF) in sodium dodecyl sulfate (SDS) micellar solution [2,3].
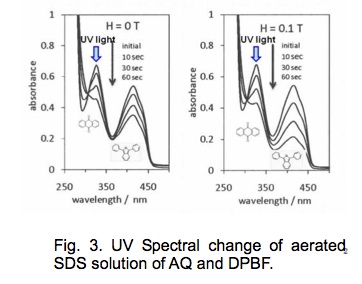
Figure 3 portrays UV spectral changes of an aerated SDS micellar solution of anthraquinone (AQ) and DPBF. Upon photo-irradiation of AQ, DPBF is oxidized to dibenzoylbenzene (DBB). In a zero field, intensities of the absorption bands of AQ (320 nm) and DPBF (410 nm) decrease gradually with irradiation time. In a 0.1 T field, the DPBF degradation is enhanced significantly. The MFE on the degradation yields of AQ and DPBF and the formation yield of DBB was examined using high performance liquid chromatography (HPLC). The results are presented in Fig. 4.
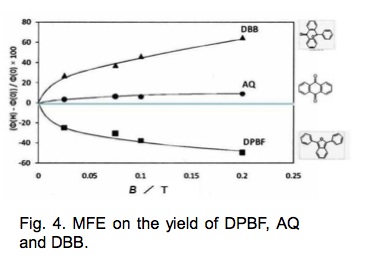
The degradation yield of AQ was reduced by 10% at 0.2 T, whereas the degradation yield of DPBF and the formation yield of DBB increased by 50–60% at 0.2 T.
Details of MFE on photochemical reaction of AQ in a de-aerated SDS micellar solution have been elucidated. The reaction mechanism of AQ is the following.


The degradation yield of DPBF and therefore the formation yield of DBB increases as the yield of oxidation initiator increases by application of MF.
2.Thermodynamic Effect – Anisotropic Magnetic Energy –
Magnetic Orientation –

Therein, χ is the magnetic susceptibility of the molecule. Usually a molecule has anisotropic magnetic susceptibilities. Therefore, the magnetic energy is orientation-dependent and the molecule undergoes molecular orientation to the most stable direction. However, the magnetic energy of a molecule is extremely small compared to the thermal energy at room temperature. Consequently, no orientation of a single molecule is achieved at room temperature. In contrast, aggregates that have an ordered structure such as crystal can obtain anisotropic magnetic energies greater than the thermal energy at room temperature because the anisotropic energy of an aggregate increases concomitantly with increasing volume, whereas its translational thermal energy, randomizing its orientation, is constant, irrespective of volume.
Magnetic orientation of carbon nanotubes [6].
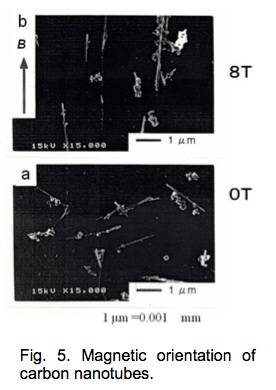
Figure 5 depicts carbon nanotubes prepared from their solution suspension using solvent evaporation. At a zero field, carbon nanotubes (white lines in the figure) are oriented randomly. In an 8 T field, they are oriented in parallel to the field. The magnetic orientation of carbon nanotubes is achieved even though they are as short as a few micrometers.
3. Mechanical Effect – Lorentz Force

MFE on silicate garden (chemical garden) reaction [4,5]. The silicate garden reaction is a famous reaction that is used popularly for chemical demonstrations. The reaction is simple. When metal salt crystals are put into an aqueous solution of sodium silicate, they grow upward in the solution in semi-permeable tubes within an hour or so.
![]()

A concentrated solution of metal salt flows out from the top of the tube. The motion of ions in the solution is affected by the Lorentz force. The direction of the helix is determined by the relative relation between the tube and the vessel wall.
4. Mechanical Effect − Magnetic Force and Magnetic Susceptibility Force

a. Magnetic Force, Magnetic Levitation, and Magnetically Simulated Microgravity
Magnetic force
Many examples of this effect exist. Here, the simplest example is introduced.
MFE on silver crystal growth [7]. When copper metal is immersed in a silver nitrate aqueous solution, metallic silver crystals deposit from the solution because of their ionization tendency.
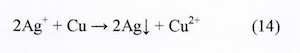
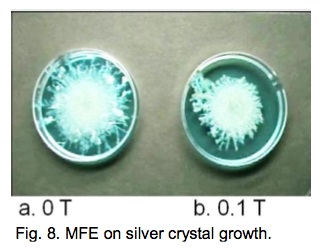
Figure 8 portrays the MFE on the shape of silver crystal in a petri dish (diameter50 mm). In a zero field, large silver crystals grow freely around a circular copper metal (φ 18 mm). When the reaction is undertaken on a 0.1 T circular permanent magnet (φ 30 mm), the crystal growth is limited within the region where the magnetic field is active. Magnetic force prevents the solution containing paramagnetic Cu2+ ion from removal from the MF-active region.
Magnetic levitation
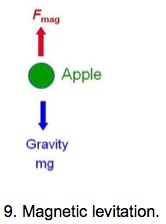
An apple falls downward because of gravity. If an upward magnetic force equals to the gravitational force is applied, then the apple is levitated (Fig. 9).


Figure 10 shows a magnetically levitated water droplet containing a sludgeworm, as viewed from the side [8]. We can levitate many diamagnetic substances such as water, frogs, cherry tomatoes, and plastic chips.
Magnetically Simulated Microgravity We can generate magnetically simulated microgravity on the earth using MF because the effective gravitational force becomes zero under the conditions given in eq. 15.
For example, we were the first to report preparation of lysozyme crystals having X-ray-crystallographically improved quality using a superconducting magnet [9]. It is worth remembering that magnetically simulated microgravity is an environment that is analogous to a space environment, but not the same because there might exist MFEs of several types. Such environments are anticipated for preparation of new functional materials using magnetically simulated microgravity.
b. Magnetic Susceptibility Force
The effect of a horizontal magnetic field (8 T) on the growth rate of glycine crystal from aqueous solution was examined [10]. The rate decreases by about 20% by application of the homogeneous magnetic field. Glycine is amino acid, having no net charge. Therefore, neither Lorentz force nor magnetic force can affect the growth rate. When approaching conditions in which the crystal concentration of glycine becomes non-uniform, some glycine in the solution is deposited as crystals on the crystal surface. It is proposed that the growth rate of glycine crystal is reduced by the magnetic susceptibility force, which prevents the convection necessary for solute transportation from the bulk solution to the crystal surface.
5. Biological Effects of MF
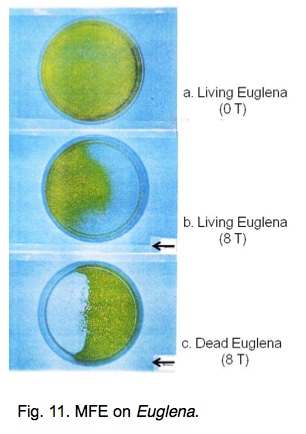
Finally, MFE on the behavior of a microorganism, Euglena gracilis is discussed [11]. In the absence of a magnetic field, living Euglena in water disperse uniformly in a petri dish (Fig. 11). When an 8 T horizontal magnetic field is applied, living Euglena move to a higher field after a few hours of exposure, although dead ones move to a lower field. This observation is explainable by the magnetic orientation of Euglena.
6. Summary
As described briefly herein, MF presents great possibilities for affecting various chemical, physical, and biological phenomena. Furthermore, several interesting effects of MF, the mechanisms of which are not explainable using the mechanisms shown in Table 1, have been reported. New MFEs will be discovered in the near future.
Magneto-science will become a key basic science supporting materials sciences, nano- and life-sciences, etc. in the twenty-first century because it presents the promise of many far-reaching technological applications to various areas of industry.
References
[1] M. Yamaguchi and Y. Tanimoto (Eds.), Magneto-Science, Kodansha/Springer, Tokyo, 2006.
[2] Y. Tanimoto, K. Shimizu, and M. Itoh, J. Am. Chem. Soc., 106, 7257 (1984).
[3] C. Udagawa, T. Izutani, S. Yamamoto, S. Morimoto, S. Fukuyoshi, R. Nakagaki, and Y. Tanimoto, J. Photochem. Photobiol. A: Chem., 238, 16 (2012).
[4] I. Uechi, A. Katsuki, L. Dunin-Barkovskiy, and Y. Tanimoto, J. Phys. Chem. B, 108, 2527 (2004).
[5] W. Duan, S. Kitamura, I. Uechi, A. Katsuki, and Y. Tanimoto, J. Phys. Chem. B, 109, 13445 (2005).
[6] M. Fujiwara, E. Oki, M. Hamada, Y. Tanimoto, I. Mukouda and Y. Shimomura, J. Phys. Chem. A, 105, 4383 (2001).
[7] Y. Tanimoto, C. Udagawa, A. Katsuki, S. Maki, and S. Morimoto, Bull. Chem. Soc. Jpn., doi:10.1246/bcsj.20130168
[8] HYPERLINK "http://www.magneto-science.jp/english/gallery_en.html" http://www.magneto-science.jp/english/gallery_en.html
[9] D. C. Yin, N. I. Wakayama, K. Harata, M. Fujiwara, T. Kiyoshi, H. Wada, N. Niimura, S. Arai, W. D. Huang, and Y. Tanimoto, J. Cryst. Growth, 270, 180 (2004).
[10] M. Sueda, A. Katsuki, Y. Fujiwara, and Y. Tanimoto, Sci. Tech. Adv. Mat., 7, 380 (2006).
[11] Y. Tanimoto, S. Izumi, Y. Fujiwara, M. Fujiwara, T, Hirata, and S. Yamada, Int. J. Electromag. Mechanics, 14, 311 (2001/2002).