Research
Optical quantum networks
Optical quantum networks are composed of photon emitters, photon detectors, and optical elements that transform the optical mode structure to implement quantum oprations on the N-photon states. Experimental tools include lasers, entangled photon sources, single photon detectors, and elements of linear optics such as beam splitters, polarizers, waveplates, etc. By combining these optical components, it is possible to build up a system that can process quantum states defined at the level of individual photons. The combination of optical coherence and single photon detection permits the most detailed and precise characterization of quantum processes achievable with present technology. Optical quantum technologies are therefore a nearly perfect experimental toolbox for the investigation of fundamental quantum phenomena and their potential applications. Two examples from our present research are given below.
☆Quantum measurements
Most
traditional approaches to quantum mechanics give very little
consideration to the actual measurement process, giving the rather
misleading impression that measurements just ``happen'' at the end
of a
quantum process. However, quantum technologies allow us to control
the
details of the measurement process much better than the crude
realizations of measurement by particle detection. In particular, it
has been recognized that new insights into quantum statistics can be
gained in the limit of weak measurements, where the interaction is
so
low that the original state of the system is undisturbed. It is then
possible to bypass the uncertainty limits of quantum measurements to
obtain joint
information about physical properties that cannot be measured
jointly in a well-resolved strong measurement.
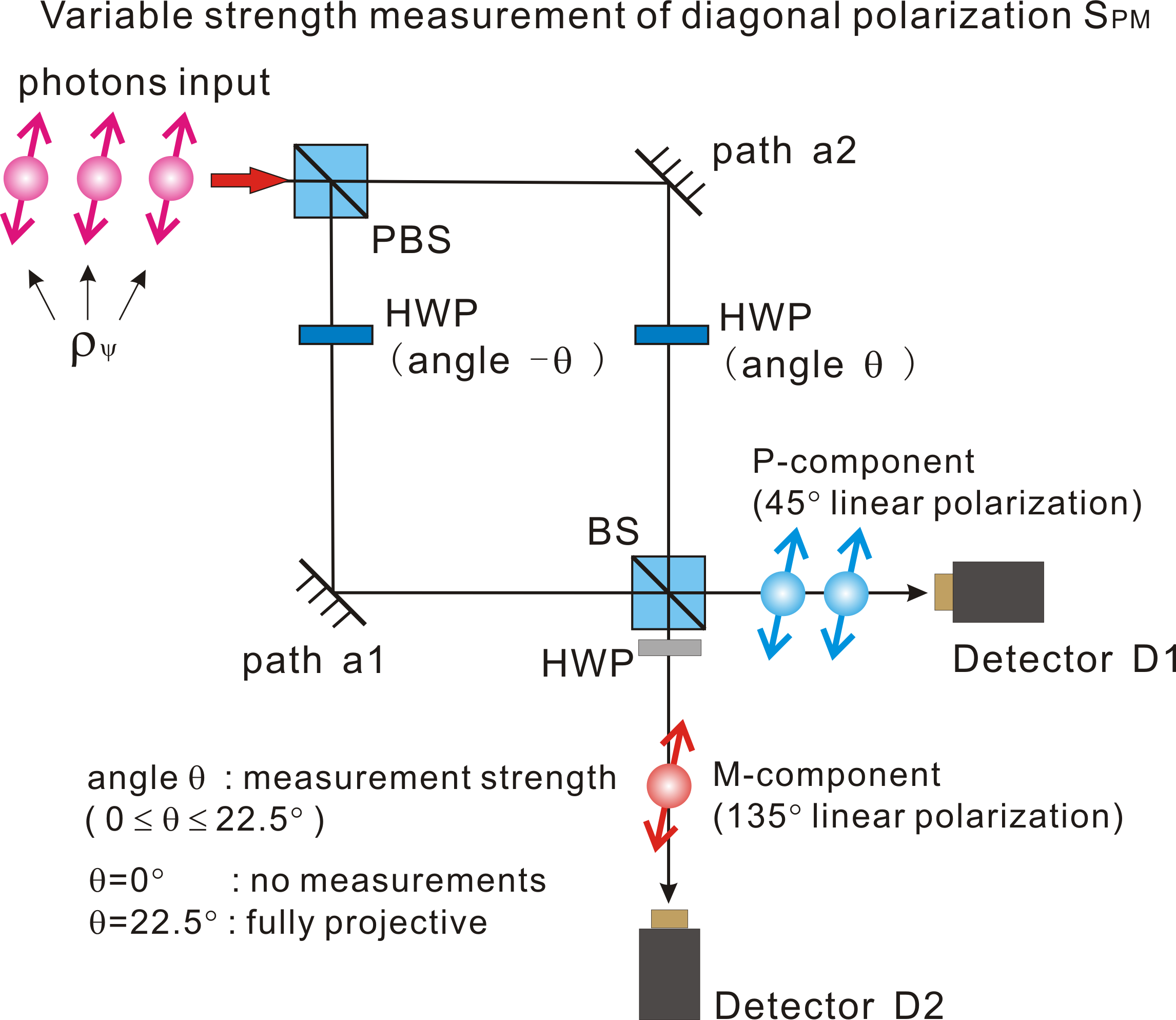
In our recent research, we have carried this approach one step
farther
by considering the statistical effects of measurement back-action in
a
variable strength measurement. As shown in the figure below, we
realized a simple interferometric setup, where the interaction is
realized by interference at a beam splitter. By rotating the half
wave
plates in the path, we determine how strongly the polarization
couples
to the interfering paths, thereby gaining optimal control of the
measurement strength. Our analysis of the experimental results shows
that the weak measurement statistics of the input can be obtained
with
even better precision at intermediate measurement strengths if the
statistics of back-action errors is taken into account. A better
understanding of the measurement process therefore shows that weak
measurements are merely a specific limit of a more general
experimental
characterization of quantum statistics based on weak-valued joint
probabilities.
☆Optical non-linearities at the quantum level
One drawback of present optical techologies is that non-linear effects usually require very strong fields with more than just a few photons. To realize the full potential of optical quantum networks, it would be useful to develop an optical device that can implement a fully coherent non-linear interaction between only two photons, or between a coherent state and a single photon. Since optical non-linearities originate from the changes in the optical properties caused by polarization and excitation of a medium, we have focussed on the non-linearity of a single few-level atom efficiently coupled to a light field freely propagating in one dimension, corresponding to the coupling achieved by a micro cavity using the enhancement of emission through the cavity mode to suppress scattering losses. Our theoretical analysis shows a variety of interesting dynamical effects that introduce quantum statistical patterns such as temporal entanglement in the interaction. While these effects make it difficult to perform simple operations on photon polarizations or paths, it may be possible to develop better strategies for non-linear implementations at the quantum level by improving our understanding of the actual physics involved in the processes.
| Overview
of our research |
||
| What is so special about quantum physics ? | ||
| Optical quantum networks | Non-classical correlations | Explanation of quantum phenomena |