Research
Non-classical correlations
☆Joint operations on non-commuting observables
Quantum
mechanics describes physical properties in terms of states and
operators. Unless a precise measurement is performed, it is
difficult
to identify the effects of a property with a specific (eigen-)value
of
that property. However, quantum statistics often involves
statistical
correlations between properties that cannot be measured jointly. One
well-known example is the case of entangled states, where all
physical
properties of one system can be perfectly correlated with all
physical
properties of another system. It is then possible to explore
correlations between non-commuting properties by using the remote
system as a kind of reference. Similar effects are exploited in
quantum
networks to achieve higher precision or more efficient processes for
quantum computation. In our group, we are searching for new ways to
explore the physics of non-classical correlations.
☆Investigation of operator statistics in quantum processes
One approach towards a better understanding of non-classical
correlations is the theoretical analysis of quantum protocols based
on
the statistics described by operators. In recent work, we have shown
that quantum correlations play a very specific role in both quantum
teleportation and quantum cloning, where they replace the roles that
classical correlations would play if these processes were applied to
classical statistics. We can show that neither teleportation nor
cloning should be interpreted as a process that copies the "state".
Instead, teleportation and cloning actially copy the values of all
physical properties equally. A proper description of quantum
fluctuations is therefore essential for our understanding of
non-classical correlations.
☆Direct observation of non-classical correlations by sequential
measurements
In quantum measurements, an error free measurement of two
non-commuting
observables is impossible, since the most precise measurements are
projections onto eigenstates, and there are no joint eigenstates for
non-commuting observables. Experimentally, this means that a
measurement of one observable must necessarily disturb the values of
the other, so as to introduce the theoretically predicted errors in
a
final measurement of this property. However, this does not mean that
the non-classical correlations are lost - they are merely modified
(and
usually weakened)
by the statistical noise that characterizes the back-action. It is
therefore possible to directly identify the non-classical
correlations
in the actual measurement data obtained from a sequential
measurement.
The concept is shown in figure 1: the sequential measurement returns
two results, (a,b), corresponding to a simultaneous assignment of
eigenvalues to two operators A and B. However, there is a
statsitical
background noise caused by the finite resultion of the measurement
of A
and the back-action that sometimes changes the value of B. As we
have
shown in our research, it is sometimes possible to identify the
precise
magnitude and pattern of this error background, so that the signal
of
non-classical correlations can be separated from the noise of the
measurement uncertainties in an almost classical manner.
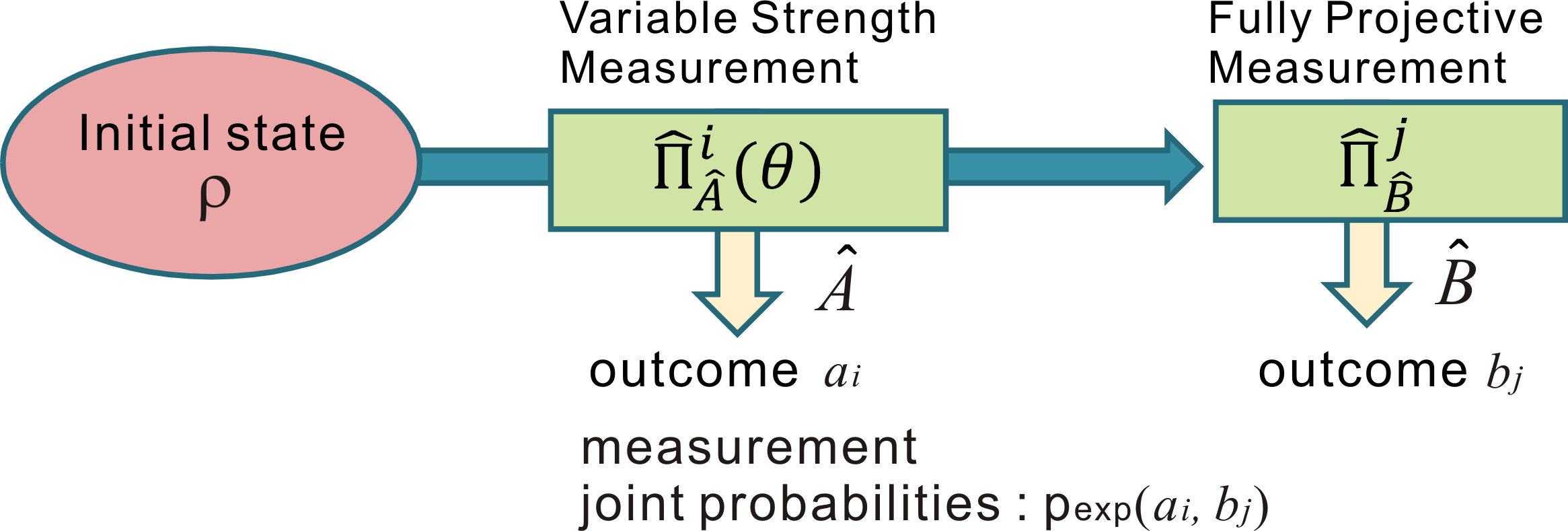
Figure 1: Concept of seqeuntial measurement of observable A and B
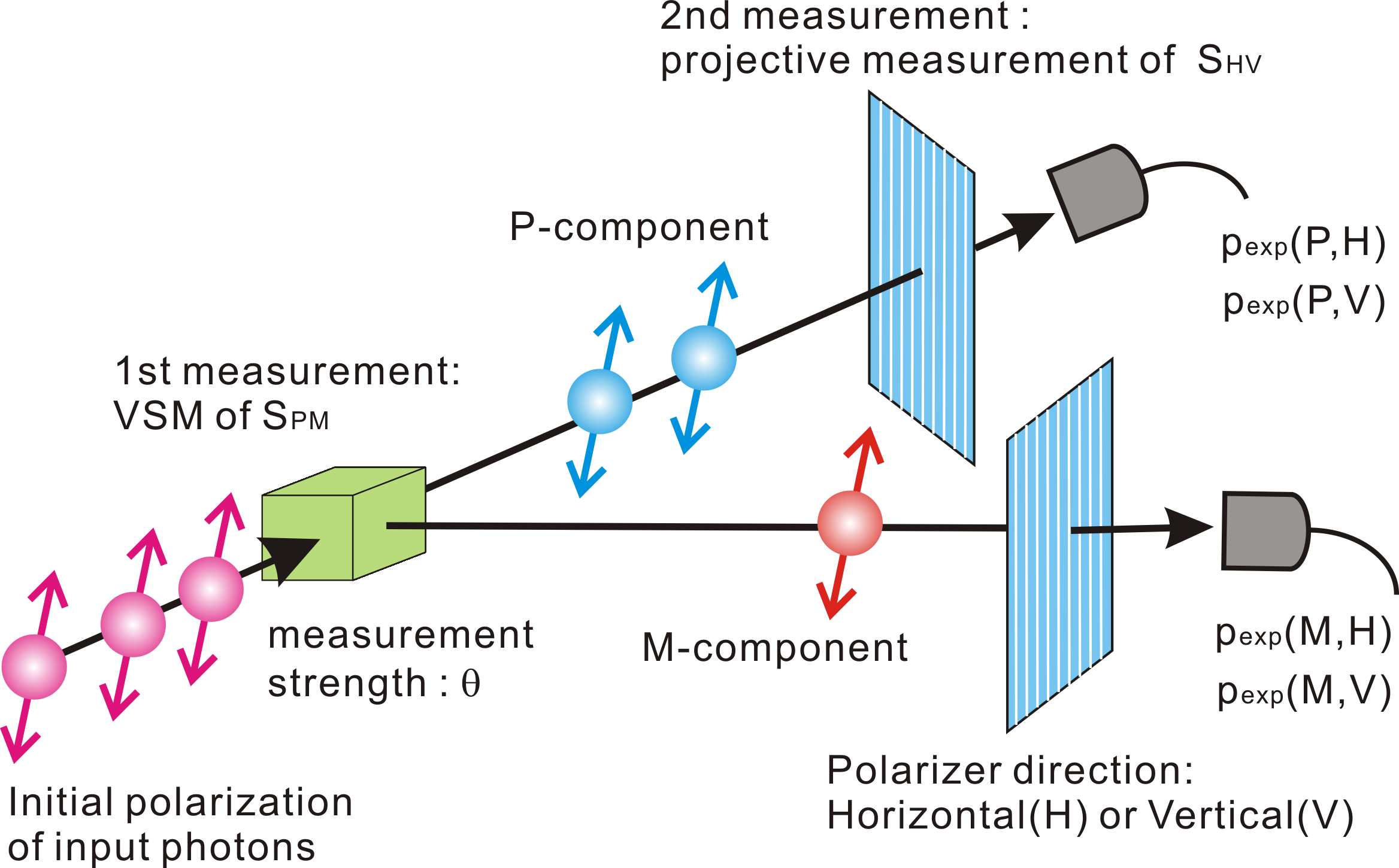
Figure 2: An example of sequntial measurement of SPM and SHV in case of photon polarization
| Overview
of our research |
||
| What is so special about quantum physics ? | ||
| Optical quantum networks | Non-classical correlations | Explanation of quantum phenomena |