オイラー法
今日の演習
- 1階常微分方程式の数値解法(オイラー法)
今日の目標
- 1階常微分方程式を解く方法を知る
常微分方程式の数値解法
次のような常微分方程式の初期値問題を、オイラー法を用いて数値的に解き、gnuplot を用いて結果をグラフにしてもらいます.オイラー法に関しては、 課題として予習してもらいましたので、ここでの内容はその復習となっています. (多少、記号の書き方が違うかもしれません.)
次の初期値問題を考えます.
(1) 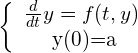
求めたいのは、![]() の範囲の関数
の範囲の関数![]() であり、関数
であり、関数![]() および定数
および定数![]() は与えられているとします.
は与えられているとします.
また、![]() の値は
の値は![]() が与えられればいつでも計算できるものとします.
が与えられればいつでも計算できるものとします.
(プログラム中では関数として定義するとよい.)
コンピューターでは数値を離散的に(とびとびに)しか扱うことができません.
そこで、(1)式をコンピューターで扱えるようにする必要があります.
(1)をコンピュータで解く方法には色々とありますが、この演習では代表的なオイラー法(とルンゲ・クッタ法)を用います.
その前に、準備として差分商について説明します.
差分商
![]() を
を![]() の関数としたとき、
の関数としたとき、![]() の
の![]() における微分係数は
における微分係数は
(2) ![]()
で定義されます.ここで、定義中の極限操作を取り払い、![]() を有限にとどめた
を有限にとどめた
(3) ![]()
を考えると、h を十分小さな正の実数にとれば、(3)式は(2)式の近似となっていると考えられます.
この D のように、関数のいくつかの点における値の差を用いて、その関数の微分係数を近似することを差分近似といい、(3)式の右辺のような量を差分商といいます.
いまの場合は1階微分係数を近似する1階差分商です.
では、このような差分商を用いて(1)式を離散化してみましょう.
まず、(1)式の第一式の微分係数を上記の差分商で置き換えてみます.
(4) ![]()
ただし、![]() は正の数とします.
は正の数とします.
(4)式と(1)式の第一式は異なる方程式なので、(1)式の第一式の解 ![]() は一般に(4)式を満たしません.
は一般に(4)式を満たしません.
そこで、混乱を防ぐために(4)式の![]() を
を![]() と書き換えましょう.
と書き換えましょう.
(5) ![]()
(5)式のように差分を含む方程式を差分方程式といいます.
次に、(1)式の![]() を
を![]() に置き換えた初期条件
に置き換えた初期条件
(6) ![]()
の下で(5)式を解くことを考えます.(5)式は、
(7) ![]()
と変形できるので、![]() を代入すると、
を代入すると、
(8) ![]()
となり、![]() から直ちに
から直ちに![]() が求まります(注意:
が求まります(注意:![]() は初期条件として与えられているので既知).
は初期条件として与えられているので既知).
同様にして(7)式を繰り返し用いると、
(9) 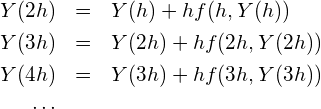
というように、![]() とすると
とすると![]() を
を![]() から計算できることがわかります.
から計算できることがわかります.
![]() をいったん決めると、
をいったん決めると、![]() 以外の時刻の
以外の時刻の![]() の値は(7)式からは求めることができません.
の値は(7)式からは求めることができません.
このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります.そのようなとびとびの時刻を格子点と呼びます.
![]() は格子点でのみ意味があるので、そのことを明示するために
は格子点でのみ意味があるので、そのことを明示するために![]() を
を![]() と書き換え、
と書き換え、![]() とすると、(5)式と初期条件は、
とすると、(5)式と初期条件は、
(10) 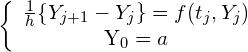
となり、結局(1)式の常微分方程式の初期値問題が、![]() に関する漸化式の問題(10)式に置き換えられました.この方法をオイラー法と呼びます.
に関する漸化式の問題(10)式に置き換えられました.この方法をオイラー法と呼びます.
オイラー法のアルゴリズム
解を求める時刻の上限を T (下限は 0 )とし、適当な自然数 N (格子点の数) を定めて h=T/(N-1) とする
(N…時間刻み数、h…時間刻み幅 ).
T, h, a, t(時刻),Y(ある時刻での値), Y_new(次の時刻での値)及び 関数 f は実数型(floatよりもdouble推奨)
N, j は整数型(int)
.(10)式の Yj, Yj+1, Yj+2, … を、 「Yj の値から Yj+1 を求める。」、「次に Yj+1 の値から Yj+2 を求める。」、「次に…。」… と求める代りに、,Y(ある時刻での値), Y_new(次の時刻での値)を使って
「Y から Y_new を求める。(例えば Y が Yj に, Y_new が Yj+1 に対応)」、「Y を Y_new で置き換える。」、
「Y から Y_new を求める。(今度は Y が Yj+1 に, Y_new が Yj+2 に対応)」、「Y を Y_new で置き換える。」、…、
という繰り返しで求める.
(例1)
Y の初期値 a を設定 (#define 文)
時刻の上限 T(下限は 0 ), 時間刻み数(格子点数) N を設定(#define 文)
時間刻み幅 h = T/(N-1) を設定(#define 文)
(ここから計算開始)
初期値を与える Y = a
初期時刻(t = 0)と初期値 a を画面に表示(printf関数)
各格子点での値を j = 0,1,2,.......,N-1 の順に計算 (for 文)
t = j*h
Y_new = Y + h*f(t, Y)
(一定間隔毎に)t+h と Y_new の値を画面に表示(printf関数)
次の時刻の計算のため、Y を新しく求まった値(Y_new)で置き換え
Y = Y_new
以上を繰り返す
f(t, Y) は関数として定義するとよい.
ただし,#defineを使ってしまうと,aの値の入力をキーボードから受けてとることができない.
その場合は,aをdefineせずに
また,上のプログラムは「時刻の上限Tを明示的に指定しているが,時間刻み幅hはT/(N-1)により間接的に与えている」.
hは計算の精度に直結するので,hを直接指定したい場合もあるだろう.
その場合は,「時刻の上限TはT*hと間接的に指定しているが,時間刻み幅hは直接値を指定する」
ということになる.どちらも一長一短であるので,好きに使い分けると良い.(アルゴリズムとしては同等である)
後者の記法で,なおかつ初期値をキーボードから受け取る例を下に示す.
(例2)
時刻の下限を0 , 時間刻み数(格子点数) N を設定(#define).
時間刻み幅 h を指定(陽に0.01などと指定する)(#define)
(ここから計算開始)
aの入力を促す
初期値を与える Y = a
初期時刻(t = 0)と初期値 a を画面に表示(printf関数)
各格子点での値を j = 0,1,2,.......,N-1 の順に計算 (for 文)
t = j*h
Y_new = Y + h*f(t, Y)
(一定間隔毎に)t+h と Y_new の値を画面に表示(printf関数)
次の時刻の計算のため、Y を新しく求まった値(Y_new)で置き換え
Y = Y_new
以上を繰り返す
f(t, Y) は関数として定義するとよい.
(一定時間毎に)とあるのは,例えば j が100毎に、等という意味である.つまり,
if (j % 100 == 0)
{
printf("%lf %lf\n", t+h, Y_new);
}
と いうふうにする (a % b = [a を b で割った時の余り]).これだと作成されるデータファイルの容量は1/100となる.
これは,前々回で見たように、グラフはある程度の折れ線数であれば十 分なめらかに見えるので,グラフを描く為のデータとして巨大になりすぎることを防ぐ為である.
ここで100という数値は適当に与えた物であって,グラフが十分なめらかに見えかつデータ数が小さくなるような適当な値を探す必要がある.
課題1
常微分方程式の初期値問題
![]()
を解け.
オイラー法を用いて 時刻 0≦ t ≦20 の範囲での解を求めるプログラムを作成せよ.
時刻 0≦ t ≦20 の範囲を20000等分割して(N = 20000)、100ステップ毎に printf関数により、t および y の値を表示し,それを gnuplot でグラフ化せよ.
また手計算にて解を求め、数値計算結果が正しいか確認せよ.
課題2
次の常微分方程式の初期値問題をオイラー法を用いて解いて、![]() と
と![]() の関係を gnuplot でグラフ化せよ.
の関係を gnuplot でグラフ化せよ.
(1)![]() (時刻 0≦ t ≦2 の範囲を20000等分割、100ステップ毎に値を表示)
(時刻 0≦ t ≦2 の範囲を20000等分割、100ステップ毎に値を表示)
(2)![]() (時刻 0≦ t ≦20 の範囲を20000等分割、100ステップ毎に値を表示)
(時刻 0≦ t ≦20 の範囲を20000等分割、100ステップ毎に値を表示)
(3)![]() (時刻 0≦ t ≦10 の範囲を10000等分割、100ステップ毎に値を表示)
(時刻 0≦ t ≦10 の範囲を10000等分割、100ステップ毎に値を表示)
(4)![]() もしくは y(0) = -0.1 (時刻 0≦ t ≦20 の範囲で時間刻み幅h=0.001、100ステップ毎に値を表示)
もしくは y(0) = -0.1 (時刻 0≦ t ≦20 の範囲で時間刻み幅h=0.001、100ステップ毎に値を表示)
今日学んだ事
- オイラー法による常微分方程式に数値解法