計算数理A演習第7・8回 – Masashi Shiraishi Homepage

今日の演習

常微分方程式の数値解法　（ルンゲ・クッタ法）
2階常微分方程式の数値解法（ルンゲ・クッタ法）
課題色々
振動いろいろ
減衰振動
強制振動
自然界の振動

１階常微分方程式の数値解法（ルンゲ・クッタ法）

今回は次のような常微分方程式の初期値問題を、ルンゲ・クッタ法と呼ばれる方法を用いて数値的に解いて結果をグラフにしてもらいます。

(1) $\begin{align*}\frac{dy}{dt} &= f(t,y) \\y(0) &= a\end{align*}$

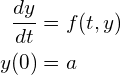
前回まではオイラー法を用いた数値解法の演習を行いました。
オイラー法は単純でそれはそれでよいのですが、実際の解に近い数値解を出すためには、時間刻み幅 $h$ をかなり小さくとらねばならないことが課題の結果からわかりました。
そこで、より精度の高い解法が必要となりますが、今回はそのような解法として、ルンゲ・クッタ法を扱い、それを用いた数値解法の演習を行います。

ルンゲ・クッタ法の導出については、このページの最後を参照してください（詳細は参考書を参照してください）。
ルンゲ・クッタ法は次に示すアルゴリズムで、オイラー法に比べれば多少複雑なものとなっています。
比較の為に両方のアルゴリズムを載せておきます（赤字の部分が異なります）。
よく比較してください。

オイラー法

ルンゲ・クッタ法

T ：解を求める時間の上限
h ：時間刻み幅
N ：時間刻み数
y：変数
a：初期値
y_new：実数型の変数

T ：解を求める時間の上限
h ：時間刻み幅
N ：時間刻み数
y：変数
a：初期値
y_new, r_1, r_2, r_3, r_4 ：実数型の変数

T,N,h を定める
a の入力を受ける(input関数とfloat)
y = a

i = 0,1,2,….,Nの順に
t = i*h

y_new = y + h*f(t,y)

y = y_new

一定間隔毎にグラフを描画

(ax.set_data関数とplt.pause関数)
を繰り返す

f(t,y) は関数として定義するとよい.

T,N,h を定める
a の入力を受ける (input関数とfloat)
y = a

i = 0,1,2,….,Nの順に
t = i*h

r_1 = f(t, y)
    r_2 = f(t + h/2, y + (h/2)*r_1)
    r_3 = f(t + h/2, y + (h/2)*r_2)
    r_4 = f(t + h, y + h*r_3)
    y_new = y + (h/6)*(r_1 + 2*r_2 + 2*r_3 + r_4)

y = y_new

一定間隔毎にグラフを描画

(ax.set_data関数とplt.pause関数)

を繰り返す

f(t,y) は関数として定義するとよい.

＊オイラー法では, （とびとびの）時刻 t = jh での値 y から次の（とびとびの）時刻 t = (j+1)h での値 y_new を直接計算しています。
本来、微分方程式では時刻は連続ですが、この場合は時刻 t = jh ～ (j+1)h の間の事は一切考慮されておらず、その分誤差が現れてきます。

＊ルンゲ･クッタ法では, この t = jh ～ (j+1)h の間の情報を (r_1, ～ r_4 を使って ) いくらか取り入れる事で、よりよい近似計算が可能になっています。
勿論誤差は現れるのですが、オイラー法と比べて雲泥の差です。
以下の課題でそれを確認します。

課題１

上記のルンゲ･クッタ法を用いて次の問題を解き、ルンゲ･クッタ法がオイラー法と比べて、どの程度性能が良いか比べよ。
次の初期値問題を0≦t≦5の範囲でh=0.5とし、実際にオイラー法とルンゲ･クッタ法を用いて解け。

(2) $\begin{align*}\frac{dy}{dt} &= \lambda y \\y(0) &= 1\\\lambda &= 1\end{align*}$

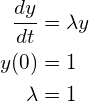
オイラー法を用いた解法プログラムをjupyter上の新しいセルに書くかeular.py上に書くとし、同問題をルンゲ･クッタ法を用いて解くプログラムを同様に新しいセルに書くかrk.pyとする。
解 y(t) = exp(t) とどの程度あっているか、一目でわかるプログラムにせよ。

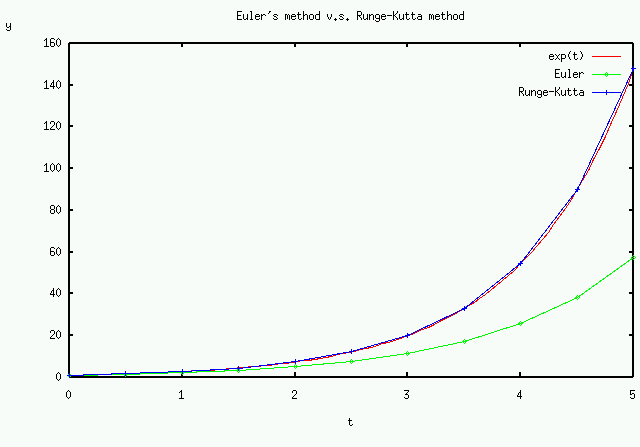
結果は大体次のようになります。
h=0.5とかなり粗く時間刻み幅をとっているにも関わらず、ルンゲ･クッタ法は良く微分解を近似できていることがわかります。
それに比べてオイラー法は微分解から大きく離れてしまっています。これでは正しい計算とは言えないでしょう。

２階（n階）常微分方程式の数値解法（ルンゲ・クッタ法）

前回の課題で扱った

(3) $\begin{align*}y''(t) &= -\omega^2 y(t) \\y(0) &= 1 \\y'(0) &= 0\end{align*}$

を $y_1(t)=y(t), y_2(t)=y'(t)$ とおいて、次のように連立の１階の常微分方程式に帰着したもの

(4) $\begin{align*}y_1'(t) &= y_2(t) \\y_2'(t) &= -\omega^2 y_1(t) \\y_1(0) &= 1 \\y_2(0) &= 0\end{align*}$

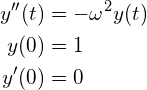
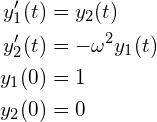
を再び考えます。
このような連立の常微分方程式をルンゲ･クッタ法を用いて解く場合のアルゴリズムを次に示します。

2階常微分方程式のルンゲ・クッタ法

T ：解を求める時間の上限
h ：時間刻み幅
N ：時間刻み数
Y1, Y2：変数
a1, a2：初期値
Y1_new, Y2_new, r1_1, r1_2, r1_3, r1_4, r2_1, r2_2, r2_3, r2_4 ：実数型の変数

T,N,h を定める
a1, a2 の入力を受ける(input関数とfloat)
y1 = a1
y2 = a2

i = 0,1,2,….,Nの順に

t = i*h

r1_1 = f1(t, y1, y2)
r2_1 = f2(t, y1, y2)

r1_2 = f1(t + h/2, y1 + (h/2)*r1_1, y2 + (h/2)*r2_1)
r2_2 = f2(t + h/2, y1 + (h/2)*r1_1, y2 + (h/2)*r2_1)

r1_3 = f1(t + h/2, y1 + (h/2)*r1_2, y2 + (h/2)*r2_2)
r2_3 = f2(t + h/2, y1 + (h/2)*r1_2, y2 + (h/2)*r2_2)

r1_4 = f1(t + h, y1 + h*r1_3, y2 + h*r2_3)
r2_4 = f2(t + h, y1 + h*r1_3, y2 + h*r2_3)

y1_new = y1 + (h/6)*(r1_1 + 2*r1_2 + 2*r1_3 + r1_4)
y2_new = y2 + (h/6)*(r2_1 + 2*r2_2 + 2*r2_3 + r2_4)

y1 = y1_new
y2 = y2_new

一定間隔毎にグラフを描画 (lines.set_data関数とplt.pause関数)

を繰り返す

f1(t,y1,y2), f2(t, y1,y2) は関数として定義するとよい.

また、f1(t, y1, y2) および f2(t, y1, y2) はそれぞれ実数型の関数です。
（3）式の場合には f1 が第一式の右辺、 f2 が第二式の右辺となります。

(今回, ω = 1 とします.)

注意！：C言語の仕様の都合上，y0, y1, ynはグローバル変数の名前として好ましくない．

y_0, y_1, y_nや，Y0, Y1, Ynで代用すると良い．

課題色々

課題２

ルンゲ・クッタ法を用いて、前回の課題7と同等のアニメーションを表示するプログラムを作成せよ。
γ＝0、dt=0.1として、オイラー法との違いを確認すること。

課題3

次の連立微分方程式を適当な初期条件のもと、オイラー法かルンゲ・クッタ法で解いてください。

(5) $\begin{align*}\frac{dx}{dt} &= 1 - (1+b)x + x^2 y \\\frac{dy}{dt} &= bx - x^2y\end{align*}$

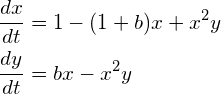
(1) b < 2 の場合
(2) b > 2 の場合

この方程式は、ブラッセレーター方程式といわれるもので、BZ反応と呼ばれる、時間的に化学成分の濃度が振動するような化学反応の振動をモデル化した方程式です。(BZ 反応とは何でしょう？ http://www.chem.scphys.kyoto-u.ac.jp/nonnonWWW/kitahata/bz_1.html あたりが参考になります。)

課題4

次の連立微分方程式を適当な初期条件のもと、オイラー法かルンゲ・クッタ法で解いてください。

(6) $\begin{align*}\frac{dx}{dt} &= 3x - xy \\\frac{dy}{dt} &= -y + xy\end{align*}$

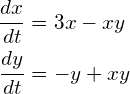
課題３の方程式同様、この方程式も振動解を見せますが、その特徴は少々違っております。
例えば初期条件を変えた場合に、これらの（課題５と課題６それぞれの）方程式系の解の振る舞いが、どのように変化していくか、見比べてください。

この方程式は、ロトカ・ボルテラ方程式といわれるもので、生態系内のある被食者と補食者の数 (x, y) 増減関係を簡単にモデル化した方程式です。
（各時刻、被食者はある割合（3x）で増えて、補食者に出会うと食べられ減る(-xy)。同様に捕食者は被食者に出会うとそれを食べて増えて(xy)、ある割合で(-y)で寿命等で減っていく。）詳しい事は各自調べてください.

課題5

　惑星の運動を考えます。万有引力の法則から２物体（質量はそれぞれ M,m）に働く力は

$\frac{GMm}{r^2}$

となります。 $r$ は２物体間の距離、 $G$ は万有引力定数で

$G \approx 6.66 \times 10^{-11} [N\cdot m^2 / kg^2]$

です。原点に太陽（質量 M）があり、惑星（質量 m）の位置を

$\vec{r}(t) = \left( \begin{array}{c} r_1(t) \\ r_2(t) \\ r_3(t) \end{array} \right)$

とします。惑星に働く力は

$\vec{F} = - \frac{GMm}{|\vec{r}(t)|^2}\cdot \frac{\vec{r}(t)}{|\vec{r}(t)|} = -GMm\frac{\vec{r}(t)}{|\vec{r}(t)|^3}$

となり，

$\vec{F} = m\vec{a} = m\vec{r}''$

より

$g = GM$

とおくと、２階の常微分方程式の初期値問題

(7) $\begin{align*}\vec{r}''(t) &= -g \frac{\vec{r}(t)}{|\vec{r}(t)|^3}\\\vec{r}(0) &= \vec{r}_0\\\vec{r}'(0) &= \vec{v}_0\end{align*}$

が得られます。これを１階の常微分方程式系に直して数値計算で解をもとめて下さい。（まずは r3 を考えずに, r1 – r2 平面上の運動方程式として考えてもよろしいです.）

課題6

水星は太陽に非常に近く、その効果が公転に影響するため、その運動は以下のような方程式に従うようになる。

$\frac{d^2\vec{r}(t)}{dt^2} = -g\frac{\vec{r}(t)}{|\vec{r}(t)|^3} + h\frac{\vec{r}(t)}{|\vec{r}(t)|^4}$

数値的に解をもとめてください。ただし、 $h \ll g$ とします。

ルンゲ・クッタ法について

簡単にルンゲ･クッタ法について説明します。演習で取り扱ったルンゲ･クッタ法は４段公式とよばれるものですが、ここでは簡単の為、２段公式を取り扱います。

次の常微分方程式の初期値問題の数値解を求めたいとしましょう。

(R1) 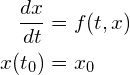$\begin{align*}\frac{dx}{dt} &= f(t, x) \\x(t_0) &= x_0\end{align*}$

２段公式とは、 $t=t_n$ で（R1）の近似解 $x_n$ が求められたとして、時間ステップ幅 $h$ だけ進んだ $t_{n+1}=t_n + h$ における値 $x_{n+1}$ を次の形で計算する公式です。

(R2) $\begin{align*}x_{n+1} &= x_n + (\gamma_1 k_1 + \gamma_2 k_2) \\k_1 &= hf(t_n, x_n)\\k_2 &= hf(t_n+\alpha h, x_n+\beta k_1)\end{align*}$

つまり、 $x_n$ から $x_{n+1}$ へ進む１ステップにおいて方程式（R1）の第一式の右辺の $f(t, x)$ を２回計算するので、２段公式と呼びます。
この２段公式には、パラメータ $\alpha, \beta, \gamma_1, \gamma_2$ が含まれますが、これらは方程式（R1）の真の解 $x(t)$ のテイラー展開

(R3) $\begin{align*}x(t_n+h)=&x(t_n)+hf(t_n, x(t_n)) \\&+ \frac{1}{2!}h^2\{f_t(t_n, x(t_n)) + f_x(t_n, x(t_n))f(t_n, x(t_n))\} + O(h^3)\end{align*}$

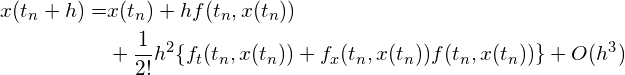
と（R2）式の第一式の同様の展開とが $h$ のなるべく高い次数の項まで一致するように定めます。
つまり、 $x_n=x(t_n)$ と仮定して（R2）式の $k_2$ の式の右辺を $f(t, x)$ 周りでテイラー展開すると、

(R4) $\begin{align*}x_{n+1}=&x_n+h(\gamma_1 + \gamma_2)f(t_n, x_n) \\&+ h^2\gamma_2\{\alpha f_t(t_n, x_n) + \beta f_x(t_n, x_n)f(t_n, x_n)\} + O(h^3)\end{align*}$

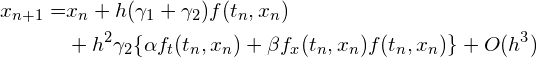
となります。
これと（R3）が $h^2$ の項まで一致するように

(R5) $\begin{align*}\gamma_1 + \gamma_2 = 1\\\gamma_2 \alpha =\gamma_2 \beta = \frac{1}{2}\end{align*}$

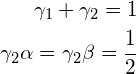
とおく。公式（R2）で定められる近似解のテイラー展開が $h$ の２次の項まで真の解のテイラー展開に一致するという意味で、この公式を２次の公式と呼びます。
この公式は２段公式でもあるので、２段２次の公式とも呼ばれます。パラメータを定める方程式（R5）には自由度が２残っているのでその定め方によって色々な公式が導かれます。（改良オイラー法、ホイン法、修正オイラー法など）
演習で用いた４段４次のルンゲ･クッタ法の公式も同様にして求めることが出来ます。

振動現象について

常微分方程式はオイラー法とルンゲ・クッタ法の二種類の解法を用いて解く事ができました。hが十分小さければルンゲ・クッタ法を用いて得た数値解（近似解）は，真の解に十分近いといえるでしょう。今回からは，ルンゲ・クッタ法を常微分方程式を解く信頼できる方法として採用し，具体的な問題を解き得られた解を見るだけでなく，現象に立ち返りその意味を再考してみましょう。（ルンゲ・クッタ法になじめない方はオイラー法を用いるのでも構いません.）

減衰振動再考

減衰振動についてもう一度考えてみましょう。

課題7

下の図のように、壁に一端を固定されたバネの他端におもりがつけられている状況を考えます。

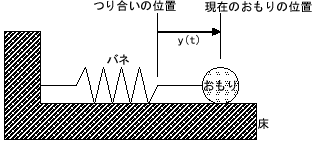
このおもりを少しだけ右に引っ張ってから手をはなす。
おもりの中心の時刻tにおけるつり合いの位置からのずれ（変位）を $y(t)$ とします。
また、時刻0でのおもりの位置を $y(0)=1$ 、おもりの速度を $y'(0)=0$ とすると次の単振動の問題となります。
（フックの法則を用いた）

(8) $\begin{equation*}\left\{ \begin{array}{rcl}y''(t) &=& -y(t) \\y(0) &=& 1 \\y'(0) &=& 0\end{array}\right.\end{equation*}$

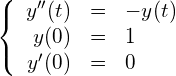
これではおもりに働く力はバネの復元力のみで、ある意味非現実的です。
今回は復元力以外におもりの速度y’に比例する抵抗が働く場合を考えましょう。
（講義ではダンパを加えた場合として説明されている）。
改良されたモデル方程式は次のようになります。

(9) $\begin{equation*}\left\{ \begin{array}{rcl}y''(t) + 2ky'(t)+\omega^2y(t) &=& 0 \\y(0) &=& 1 \\y'(0) &=& 0\end{array}\right.\end{equation*}$

ここでk，ωはそれぞれ抵抗力、復元力の強さを表す正の定数です。
（9）式の問題を連立１階常微分方程式に変換し、ルンゲ・クッタ法（オイラー法）を用いて解き可視化（グラフ）してください。
(前々回のレポートで提出されているプログラムを使い回してください。それを元に今日は現象を観察してもらいます)

以下の３通りについて，それぞれグラフを描いてください。
（例えば，ωをある値に固定して，kのみを変化させ，下記３通りを満たすようなkを選ぶとよい。３通りのグラフを色を変えて重ね描きするとよい。）

k<ωの場合：減衰振動
k>ωの場合：過減衰
k=ωの場合：臨界減衰

ところで，ドアは一種のバネ振り子＋ダンパ系と見る事ができます。
設計する際，ダンパの強さを臨界減衰になるよう設計するのが一番良いとされる。
なぜであろうか？考えてみてください。
（良いドアである為には次の二つが重要である。素早くしまる事，しまるときの音が小さい事。）

自動車やバイクのサスペンションも一種のバネ振り子＋ダンパ系であるが，おそらくはやはり臨界減衰に近いような設定が良いのであろうと考えられます，（実際にはより複雑な状況もあり，そこまで単純ではないかも知れませんが。）

強制振動

ここからは強制振動系を考えよう。
先の減衰振動系に外から周期的な外力を加える事を考える。

参考：計算数理AのHP

扱う方程式は，以下のようになる。

(10) $\begin{equation*}\frac{d^2y}{dt^2} + 2k\frac{dy}{dt}+\omega^2y=A\cos \omega_e t\end{equation*}$

見ての通り，右辺が０であれば（9）の減衰振動系となります。つまりは，（9）の減衰振動系（放っておけば減衰して静止する）に対して，外から周期的な外力を加えているのが（10）であります。

課題8

（10）を解くプログラムを作成せよ。下の図のように $y(t)$ と $A\cos \omega_e t$ 同時に表示するようにしてください.例えばパラメータ，初期値としては， $y(0)=1, y'(0)=0, k=0.1, \omega=1, \omega_e=1.3$

(11) $\begin{align*}y'(0) &= 0 \\y(0) &= 1.0\end{align*}$

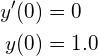
とし，時間刻み幅hはh=0.1とする。解 $y(t)$ を赤色， $A\cos \omega_e t$ を緑色で表示することにする。

A=0の場合（つまり外力が無い場合）には，

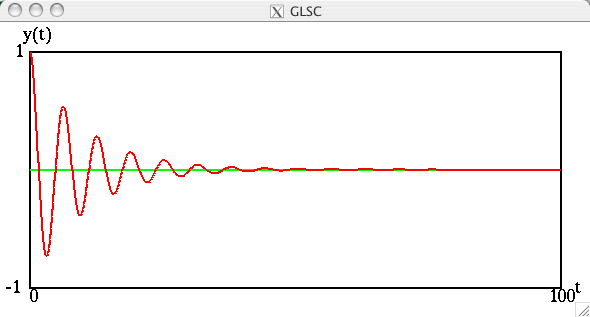
となり，当然ながら減衰振動の様子がみられる。

$A=0.1$ の場合には，

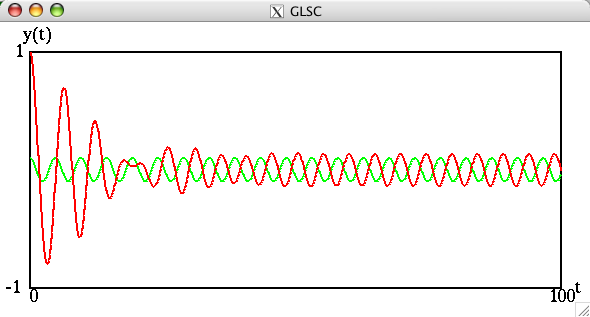
となり，過渡応答，定常応答が見られる。

$A=0.1, \omega_e=1.0$ の場合には，次のようになる。

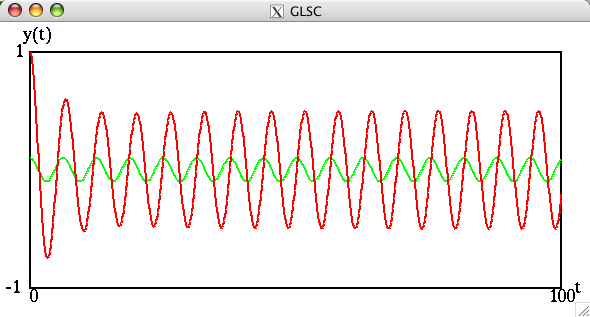
課題9

横軸をyとして，質点の動きをアニメーションで示せ。また，外力の項（ $A\cos \omega_e t$ ）の力の向きと大きさも可視化してください。

参考用動画( $k=0.1, \omega=1.0, \omega_e=1.6, A=0.1$ ）

動画中では，青いバーは $\cos \omega_e t$ を表しており，右側にあるときは右向きに，左側にあるときは左向きに外力がかかっている。
（Aの大きさを青いバーの長さに反映させるかどうかは，各自の判断に任せます。）

課題10

(1) $\omega_e =0.2, 0.4, 0.6, \cdots 2.0$ に対して， $y(t)$ と $A \cos \omega_e t$ の様子（振幅や位相の関係）を見てみよ.

(2)各 $\omega_e$ に対して， $A=0.1, 1.0, 10.0$ とした場合の $y(t)$ と $A \cos \omega_e t$ の様子（振幅や位相の関係）を見てみよ.

(3)横軸 $y$ ，縦軸 $dy/dt$ として表示し，振動の様子を見よ.

(1)(2)から分かるように，バネの固有の振動数ω(外力，抵抗が無いときの振動の周期の逆数)と，外力の振動数ω_eが近くなるにつれ，大きな振幅の振動が現れます。
これが「共鳴（共振）」と言われる現象で，例えばブランコを手で押して大きく揺らす事等は（ふつうブランコの揺れに合わせて押すことで振幅を大きくすると思いますが。），強制振動による共鳴の典型例です。
(逆にこのようなバネ系は，強く揺すってもまあそれ相応にしか振幅はふえません.外からの揺すりの「タイミング」が肝ですね.それを実感してください.)

レポート課題

課題9と同様に強制振動の式（10）を用いて，課題9のようなアニメーション
（t=0から100までのアニメーション，時刻tもwindow内に表示）を表示するプログラムrep20190509.py作成せよ。

ただし、t≧70のときは、
・t=70から現在の時刻tまでの範囲における $y$ の最小値、最大値の位置をそれぞれ縦線で図示すること。
（つまりt=80のときは $70\le t\le 80$ の範囲における $y$ の最小値、最大値の位置を縦線で図示する。）

アニメーション終了後は、また， $70\le t\le 100$ における $y(t)$ の最大値と最小値の差をDとして，そのDの値を画面に表示すること。
ただし，D=1.6（誤差は3パーセントまで許す）となるように $A$ ， $\omega_e$ を設定し， $A$ の値， $\omega_e$ の値はアニメーションのウィンドウ内に表示すること。他のパラメータ（k，ω）、初期値は課題8と同じものとする。

プログラムは関数を用いてアルゴリズムが分かりやすくなるようにしてください。
（注意点：質点の運動が画面内に収まるように座標系を設定して下さい.また $\cos \omega_e t$ を表すバーの大きさは見やすいように大きさを調整してくれてかまいません。）
Runge-Kutta法、Eular法のどちらで解いてもかまいませんが、Runge-Kutta法で解いた場合は１割程度高い点をつける予定です。

課題11

バネは大きく伸び縮みすると急激に硬くなるような場合もあります.そのようなバネに対する強制振動系として，次の微分方程式

(12) $\begin{align*}\frac{dy}{dt} &= v \\\frac{dv}{dt} &= -0.3 v - y^3+B \cos(t)\end{align*}$

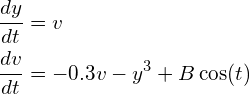
を考えます.この式を数値的に解いて、B=0，1，2，….，12，…，60…等いろいろな場合のyの時間変化を調べてください。特にy，vの初期値が少し違う場合の.yの時間変化を比較してください.課題２，３とどのような特徴の違いがあるでしょうか.（十分大きいtまでの結果を見てみてください.また横軸y，縦軸vとして表示した場合の様子も見てみてください.）

ハードディスクから原子炉まで、様々な機械の「振動」が、このような方程式を応用しながら解析されています.

自然界の振動

上記では，摩擦が働く等して放っておいたら止まってしまうようなシステム(バネ系)が，外部からの「振動（時間に依存して振動的に変化する外力）」を受ける事で定常的に振動する様子について考察しました.
しかし実際には，外からの影響が「振動的」でなくても（外力が時間変化しない.つまり方程式の右辺に「t」が現れない.），システム自身が振動的になる場合があります.そのような振動は「自励振動」と呼ばれます。
以下，自励振動の簡単な例題を見ていきます.生物を含む自然界の様々な場面で見られるいろいろな「振動（リズム）」の多くが，自励振動であります.（体内時計，脳波，生態系，為替変動，蛇口の水滴，地震，気象，..等等.*宇宙や惑星の運動等は少々違います…）