計算数学演習第５回

多重くりかえし文，while文

今日の演習

今日は以下の内容で演習を行います．

  • 繰り返し文（復習, 応用）
  • 多重繰り返し文（多重ループ）
  • 扱える数値の大きさ

多重繰り返し文（多重ループ）

for 文、while 文は入れ子にすることができます．
例えば，次のように for 文の中にさらに for 文があるような繰り返し文を、２重ループと呼びます．
もちろん、３重、４重ループも作ることができます．
次のプログラムを forfor1.c として打ち込み実行してください．
ただし、実行する前にどのような出力が出るか予想してから実行してください．
予想通りであれば、繰り返し文の理解は十分できているといえるでしょう．

 

#include <stdio.h>

int main()
{
    int i, j;

    for (i = 1; i <= 3; i++)
    {
        for (j = 1; j <= 5; j++)
        {
            printf("i=%d, j=%d\n", i, j);
        }
    }

    return 0;
}

実行すると分かりますが、多重ループでは、もっとも内側のループ（繰り返し文）が先に実行されます．

課題１

整数 i, j, が 0 ＜ i ＜ 50, 0 ＜ j ＜ 50, を満たすとする．
正の整数 n を入力すると、n = i + j を満たす全ての i, j を表示するプログラムを作成せよ．
（ヒント：２重ループと if 文）

課題２

整数 i, j, k が 0 ＜ i ＜ 50, 0 ＜ j ＜ 50, 0 ＜ k ＜ 50, を満たす．
正の整数 n を入力すると、n = i + j + k を満たす全ての i, j, k を表示するプログラムを作成せよ.

課題３

（２以上の）整数 n を入力すると、n 以下の全ての素数を表示するプログラムを作成せよ．
（前回の素数判定プログラムを利用. 繰り返し.）

while 文

while 文は次のように使われます．

while (条件)
{
    ブロック文
}

条件部分に書かれた条件式が真である間ブロック文が繰り返し実行されます．
先の for 文を使った例も while 文を使って書き換えることができて、

#include <stdio.h>

int main()
{
    int i;

    for (i = 1; i <= 10; i++)
    {
        printf("Hello!\n");
    }

    return 0;
}

は

#include <stdio.h>

int main()
{
    int i;

    i = 1;
    while (i <= 10)
    {
        printf("Hello!\n");
        i = i+1;
    }

    return 0;
}

と同等です．

このように、for 文と while 文は実質的に全く同じものです．
プログラムが見やすくなる方を選んで使えばよいでしょう．
上記２つの例では先の for 文を用いたプログラムの方が意味を理解しやすいかと思います．

例えば、次のような例では while 文が適しています．
while_1.c として打ち込んで実行してみてください.

#include <stdio.h>

int main()
{
   /* 変数の型の宣言 */
    int n, sum;

   /* 変数の初期化 */
    n = -1;
    sum = 0;

    /* n が 0 でなければ、以下の処理を繰り返す n が 0 ならば以下の処理をやめる */
    while (n != 0)
    {
       /* 変数入力 */
        printf("整数を入力してください ");
        scanf("%d", &n);
       /* 入力された数を足す */
        sum = sum + n;
    }

    /* 結果表示 */
    printf("合計=%d\n", sum);

    return 0;
}

このプログラムはキーボードから整数値を入力していき、その数字を加算します．
入力された数値が０であれば繰り返し処理を終了して合計値を表示するものです．

はじめに n = 0 とせずに n = -1　としているのは n = 0 としてしまうと、 while (n != 0) の条件式がはじめから偽となってしまうからです．
この場合 -1 という数値にはあまり意味がありません．0 でなければよいのです．

もちろん同様の動作をするプログラムを for 文を用いて作成することも可能です．

課題4

自然数Nの入力を促し，n! > Nを満たす最小の自然数nを求めるプログラムをwhile文を用いて作成せよ．
(n!はnの階乗)

扱える数値の大きさ

コンピューターは無限に大きな数値を扱うことはできません．
以下に変数が扱えるおおよその範囲を示しておきます．
（こういった話は実は機種に依存するので、注意が必要．）

データ型（変数型） 表現 範囲
int 整数型 -2147483648～2147483647
long 倍長整数型 -2147483648～2147483647
float 単精度実数型 およそ 10e-38～10e38 （有効桁７桁）
double 倍精度実数型 およそ 10e-308～10e308 （有効桁１５桁）

ここで、10eN は 10Nをあらわすとします．整数型は以外と小さな数値までしか扱えないことがわかります（20億程度）．
それでは困るので、最近のコンピューターはより大きな整数値を扱えるようになってきています．
（整数計算をする部分を自分でプログラミングすれば、いくらでも大きな整数を扱えるようになります．
例えば Mathematica などはより巨大な整数値を扱えます．もちろん、それにも限界はありますが・・．）

課題5（すこし難しめ）

    \[\frac{\pi^2}{6} - \sum_{k=1}^{N} \frac{1}{k^2} < 0.01\]

を満たす、最小のNを求めるプログラムをwhile文を用いて作成せよ。

ただし、π=3.14159とおくこと。

注意：kをintで宣言した場合、1/(k*k)の演算結果は整数となってしまう。これを回避するためには、
・整数型の変数と実数型の変数を演算（+, -, *, /）した結果は、実数型となることを利用して、1.0/(k*k)とおく
・ 1.0/( (double)(k)*(double(k)) )とおく（「定積分の近似値」のコメント参照）
などの方法がある。

定積分の近似値

積分が和の極限だということを使うと，計算機で定積分の近似値を簡単に計算できます．

以下は定積分

    \[f = \int_0^1 (1-x^2)dx\]

の近似値を求めるプログラムです．
integration-1.ｃとして打ち込み実行してください．
プログラムの概要は以下の通り。

  1. まず積分区間（0～ a）を、 n 個の、幅 d = a/n の領域に分割。
  2.  i 番目の領域の中心（x = (i+0.5)*d）での関数の値（y = 1 – x*x）を高さとする長方形の面積が = y*d と得られるので、それらを全区間に渡って足し合わせる。（紙に絵を描いてみるとすぐ分かります。）
#include <stdio.h>

int main()
{
    /* 実数型変数の宣言 */
     double f, x, y, a, d;

    /* 整数型変数の宣言 */
     int i, n;

    /* 積分範囲 を代入 */
    a = 1.0 ; 

    /* 分割数 n を代入 */
    n = 100 ; 

    /* 分割の幅 d を計算. 整数型変数 n を,ここでだけ実数型として扱って計算(下の注を参考)*/
    d = a / (double)(n) ; 

    /* fの初期化 */
    f = 0.0 ; 

    /* 積分を計算する繰り返し文 */
    for (i = 0; i < n; i++)
    {
       /* 整数型変数 i を, ここでだけ実数型として扱って計算(下の注を参考) */
       x = ((double)(i)+0.5) * d;
       y = 1.0 - x * x;
       f = f + y * d; 
    }

    /* 結果を表示 */
    printf(" 答え %f \n", f);

    return 0;
}

 

– – – – – – – – – – – – – – – –

分割数 n を大きくすると（例えば 10 -> 100 -> 1000 としていくと），2/3=0.66666・・・に近づくことを確認してください．

 注：プログラムの途中で、一時的に変数の型を変更すると便利な事があります.（上の例での n, i 等.）このような場合「(一時的に使用したい変数の型)(変数)」とすることで, 一時的にその文でのみ指定した型の変数として扱う事ができます. つまり, 例えばプログラム始めで double a; と宣言されていても, ある文中で (int)(a) 書かれていれば,その文中のみでは a は int 型変数として扱われます.（その文以外のところでは、始めに宣言された型で扱われます.）(int)(a), (double)(n) 等, 整数型, 実数型どちらでも使用可です. （例えば a = 2.9 等の場合　(int)(a) は 2 となります. 実数型変数を整数型にした場合, 小数点以下は 0 になります.）

課題６

例えば積分区間を -2 ～ 3 とした場合の定積分の近似値を計算求めよ．
また適当な関数, 積分区間でいろいろ計算してみてください.

課題７

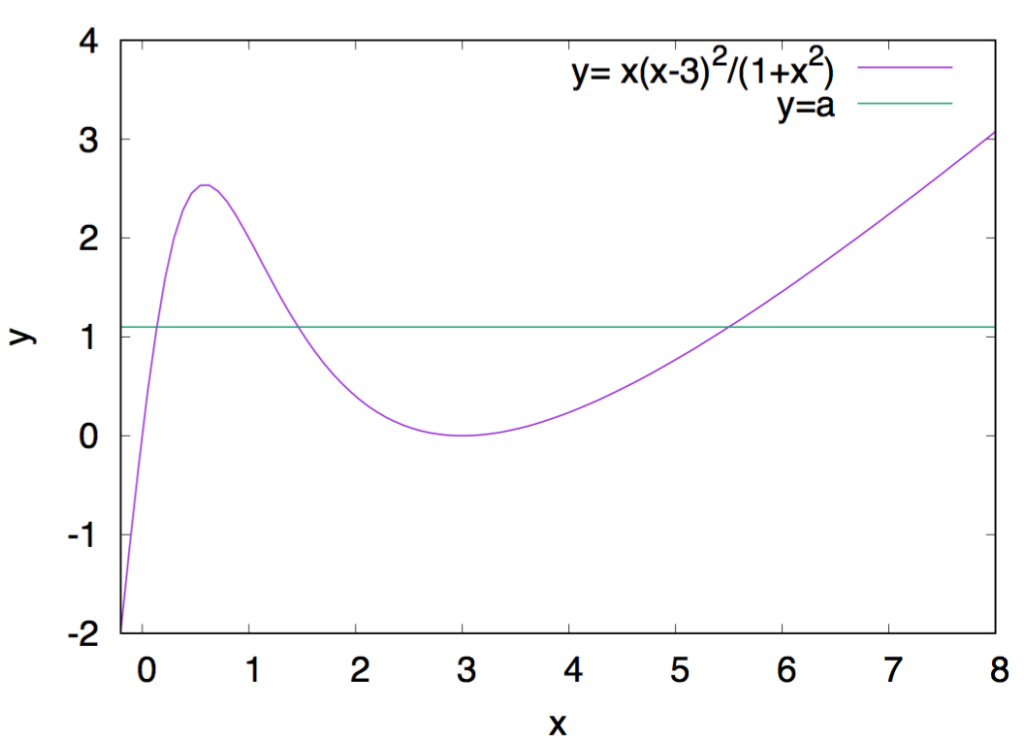
xy平面上の曲線，

    \[y = \frac{x(x-3)^2}{1+x^2}\]

とy=a　(0<a≦2)の交点をそれぞれ( x0, a), (x1, a), (x2, a)とし，
x0≦x≦x1で二つの曲線で囲まれた領域の面積をS1，
x1≦x≦x2で二つの曲線で囲まれた領域の面積をS2，
二つの面積の合計をSとする．
a=1.1のときのSを求めるプログラムを作成せよ．

レポート課題

bB9にて課題を与えます．そのままbB9上で提出するようにしてください。
３回まで提出し直せるようにしておきます．

提出締め切り：2017年11月17日(木)午後5時

プログラムの停止の仕方とファイルの消し方（前回の復習）

プログラムは正しく動作し、正しく停止することが重要ですが、停止しないプログラムを書くのは大変簡単です．停止しないプログラムはたいていの場合、プログラミングミスが原因です．例えば、次のプログラムは停止しません．．

#include <stdio.h>

int main()
{
    int i;

    for (i = 1; i >= 1; i++)
    {
        printf("Hello!\n");
    }

    return 0;
}

 

条件式 i >= 1 が真でありつづけるため停止しないわけです．（後の述べる扱える数値の大きさを超えるとおかしなことになるので、そこで停止する可能性はありますが・・．）

今後、色々なプログラムを作ってもらいますが、何らかのプログラミングミスで停止しないプログラムになっていて、それを実行してしまった場合は、

Ctrl + c
（Ctrl キーを押しながら c のキーを押す）

によって強制的に終了させることができます．覚えておいてください．

また、エラーのあるプログラムによっては core というファイル名のファイルを作成してしまう場合があります．このファイルは、当面不要なので、消してしまいましょう（ファイルサイズが大きいので）．以前、0 での割り算を行うプログラムを実行した人は、多分この core ファイルができているはずです．

今日学んだ事

  • 繰り返し文を使えるようになりました
  • より複雑なプログラムを理解し、つくることができるようになりました