gnuplotでのグラフの描画
今日の演習
今日は以下の内容で演習を行います.
- Cプログラムとgnuplotを使った、グラフ、図形の描写
今日の目標
gnuplot の使い方の基本を身につける.
gnuplot 入門
今回は、まずgnuplotと呼ばれるアプリケーションを用いて、関数やデータの可視化を行います.
このgnuplotは、手軽に使える上に様々な便利な機能があるため、学術論文等に掲載されるグラフ等の作成にも、使われています。
今回はこの gnuplot を用いて、簡単なグラフや図形の描画を実践してみます.
まず幾つかの関数をgnuplotで描画してみます.
ターミナルで,
gnuplot
と打ち込み,改行キーを押すことで gnuplot を起動することができます.
起動すると,ターミナル上のプロンプトは gnuplot のものとなり,gnuplot のコマンドを入力できる状態となります.
そこで,
plot x*x – 2
とすることにより,グラフを得ることができます.
x の範囲は自動的に決められますが,こちらで設定することもできます.
x2は x**2 と表記します.
plot [0:2] x**2 – 2
gnuplot は,
quit
で終了できます.
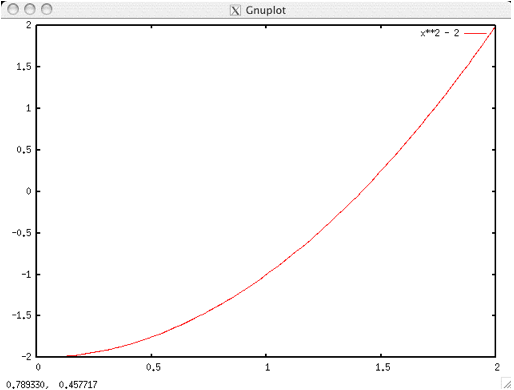
たとえば,次のようなものを試してみてください.
plot [-6:6][-1.5:1.5] sin(x) plot [-6:6][-1.5:1.5] cos(x) plot x**3 - x**2 + 5
グラフの横軸(x)、縦軸(y)の表示範囲は
plot [(min_x):(max_x)][(min_y):(max_y)] F(x)
として、min_x、 max_x、min_y、max_y を与えることで決ります。
縦軸(y)のみ範囲を与えたい場合は
plot [][(min_y):(max_y)] F(x)
とすると出来ます。
ファイル内のデータの描画(新しい内容)
次に、ファイルに書き込まれているデータからグラフを作成します。
まずdata-ex1というファイルを作成し、その中に以下のような形で数値を書き込んで下さい。
2.0 1.0 -3.0 -2.0 1.0 1.0 -2.0 -1.0 2.0 2.0 -1.0 -3.5
(注意)横に並ぶ数値の間には、必ずスペースを入れてください。
次にターミナルで、gnuplotとして gnuplot を起動し、
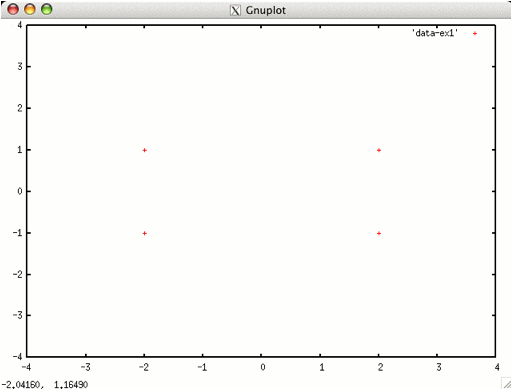
plot [-4.0:4.0][-4.0:4.0] “data-ex1”
とすると(改行キーを押すと)、以下のように、(2,1),(-2,1),(-2,-1),(2,-1)に4つ点が表示されるはずです。
ここでは見易くするために、横軸、縦軸の範囲を-4~4にしました。
gnuplotは、横に並ぶ数字の組をある一点の座標とし、表示します.
このデータファイルには、4つの点の座標が記述されていることになります.
何も指示しなければ,横軸(x軸)に一列目、縦軸(y軸)に2列目が用いられます。
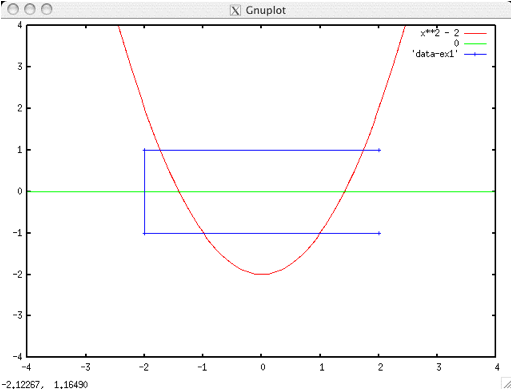
ではここで、
plot [-4.0:4.0][-4.0:4.0] “data-ex1” using 2:1
とします。すると先程と縦と横が入れ替わります。また
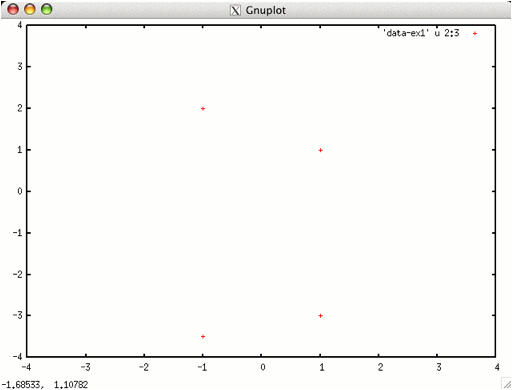
plot [-4.0:4.0][-4.0:4.0] “data-ex1” using 2:3
としますと(1,-3),(1,1),(-1,-2),(-1,-3.5)の4点が表示されます(下図)。
この場合、横軸に 2 列目、縦軸に 3 列目 の値が使われています.
「using a:b」というのが「横軸に a 列目、縦軸に b 列目を用いる」というコマンドになっています。
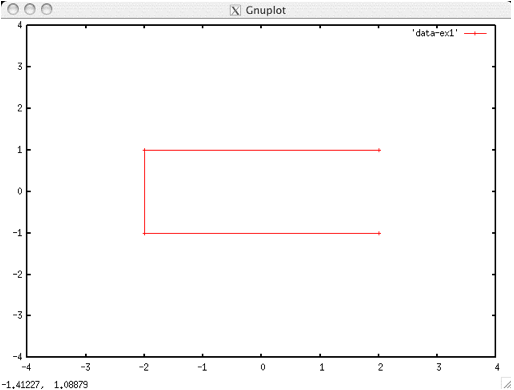
次に線を描きます.例えば
plot [-4.0:4.0][-4.0:4.0] “data-ex1” with lines
とすると、(2,1),(-2,1),(-2,-1),(2,-1)が直線で結ばれます.
この「with lines」は、点をデータファイルに書かれている順に直線で結ぶコマンドです。
また
plot [-4.0:4.0][-4.0:4.0] “data-ex1” with linespoints
とすると、4つの点とそれをつなぐ直線が描かれます.
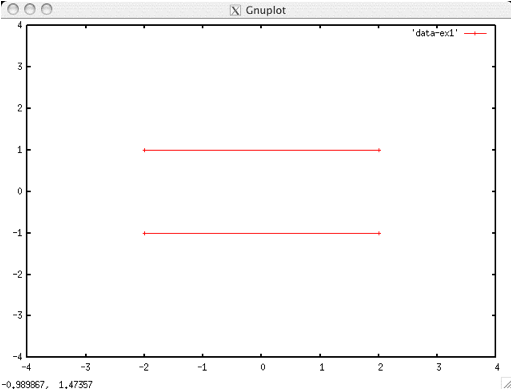
今度は以下のように一行スペースを入れます。
– – – – – – – – – – – – – – – –
2.0 1.0 -3.0
-2.0 1.0 1.0
-2.0 -1.0 2.0
2.0 -1.0 -3.5
– – – – – – – – – – – – – – – –
同じように gnuplot を起動し、
plot [-4.0:4.0][-4.0:4.0] “data-ex1” with lines
とか
plot “data-ex1” using 3:1 with lines
とすると今度は、2本の直線が現れます(下図)。
このように行を空けることで、複数の図形を描画できます。
描画のコマンドについてまとめますと、(データファイル中の a 列目をx 座標(横軸)、 b 列を y 座標(縦軸)として、それぞれ min_x ~ max_x、min_y ~ max_y の範囲で線描画(点描画)させたいとき)
plot [(min_x):(max_x)][(min_y):(max_y)] “データファイル名” using a:b with lines (points)
という順番で指定していきます.
(参考までに)
複数のファイルや関数のグラフを同時に表示させたい場合は、
plot x**2 – 2, 0, “data-ex1” w lp
というふうにカンマで区切って並べます。
ちなみに、with lines は w l、with linespoints は w lp と略せます。
y = sin(x) のグラフの描画
これから、gnuplot を使って y = sin(x) のグラフを描きます.
もちろん,gnuplot では,
plot sin(x)
とすれば y = sin(x) のグラフが得られるのですが,gnuplot がどのようにしてそれを描いているかわかりません.
そこで少々遠回りをします.
実際には y = sin(x) のグラフは滑らかな曲線ですが、コンピュータではそのような滑らかな曲線を直接は扱えませんので折れ線で近似して描画します.
つまり、変数 x は、実際には連続的に変化するものですが、とびとびの値(離散値)を使います.
後の例で見るように、とびとびとはいえ、十分に細かく取れば、折れ線で曲線をうまく近似することができます.
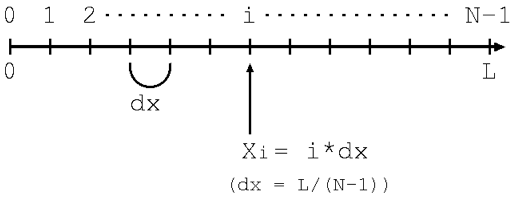
図のように [0, L] 区間を N-1 等分して、その等分した小区間の幅を dx とします.
N-1 等分すると図のように N 個の区切りが現れますが、それらに 0,1, …., i, …., N-1 と番号をつけることにします.
また、 Nを分割数、dxを分割幅と呼びます.このとき、
Xi = i*dx
の部分についてそれぞれ y = sin(Xi) を計算し、それらを折れ線で結ぶことを考えます.
C言語風に書けば
X[i] = dx*i;
Y[i] = sin(X[i]);
をそれぞれ求め、(X[0], Y[0]), (X[1],Y[1]), …., (X[N-1], Y[N-1]) を結ぶ折れ線を描くことになります.
これをプログラムにすると次のようになります.
(上記の説明にあわせるためにかなり無駄なことをしています.)
ファイル名を gnup-1.c として打ち込み、コンパイルして実行してみてください.
コンパイルするときには
cc gnup-1.c -o gnup-1 -lm
というふうに,-lm を付け加えて下さい.(下の補足2を参照)
#include <stdio.h>
/* 次の文は数学関数を使う場合に必要 */
#include <math.h>
/*** 定数の定義 ***/
#define N (5)
#define PI (3.1415926)
#define L (2*PI)
int main()
{
int i;
double X[N], Y[N], dx;
/* 分割幅 dx を求める */
dx = L/(N - 1);
/* X[i] を求める */
for(i = 0; i < N; i++)
{
X[i] = i*dx;
}
/* Y[i] を求める */
for(i = 0; i < N; i++)
{
Y[i] = sin(X[i]);
}
/* 結果を数値として表示 */
for(i = 0; i < N; i++)
{
printf("%lf %lf\n", X[i], Y[i]);
}
return 0;
}
補足1:定数(#define 文の使い方)
#define 文を使うと定数を定義することができます.
通常、#include 文の後に書きます.例えば、
#define N (5)
と書いた場合、後のプログラム中の N は全て (5) に置き換わります.
例えば、次のように使えます.
#include <stdio.h>
#define A (5)
#define PI (3.1415926)
int main()
{
printf("%d %lf\n", A, PI);
return 0;
}
#define 文は、実は単に文字列を置き換えるだけです.
つまり、printf 関数部分に A および PI がありますが、それらはコンパイル時に次のように書き換えられます.
printf(“%d, %lf\n”, (5), (3.1415926));
#define 文を上手に使うと、プラグラムが大変見通しのよいものとなります.
補足2:数学関数(三角関数等)の使い方
C言語では上記プログラムのように、三角関数等の様々な数学関数を用いることができます.
数学関数を用いる場合には、
#include <math.h> をプログラムの先頭付近に書き入れることと、コンパイル時に、ファイル名を gnup-1.c とすると、
cc gnup-1.c -o gnup-1 -lm
というふうに、最後に -lm を付け足す必要があります.
sin()の他にcos(), tan(), log(), exp()などいろいろ用意されています。
(重要)データファイルの作成・リダイレクト(本題に戻ります)
上記プログラムを使って、N とグラフの関係を見てみましょう.
まず,プログラムをコンパイルします.
cc gnup-1.c -o gnup-1 -lm
続いて実行してみましょう.
./gnup-1
とすると、数値の列が表示されます.
これら数値をgnuplotでグラフ化しましょう.
この数値の列からなる、データファイルを作成するには、次のようにします.
./gnup-1 > N=5.data
上記のようにすることで、数値列は画面に表示されず、N=5.data というファイル名のファイルが作成され、そこに書き込まれます.
(ターミナル上で、more N=5.data などとすると、確認できます. なお今回は、N=5なのでこのような名前にしましたが、ファイル名は基本的に自由です.).
gnuplot を起動し,
plot [0:2*pi] “N=5.data” with linespoints, sin(x)
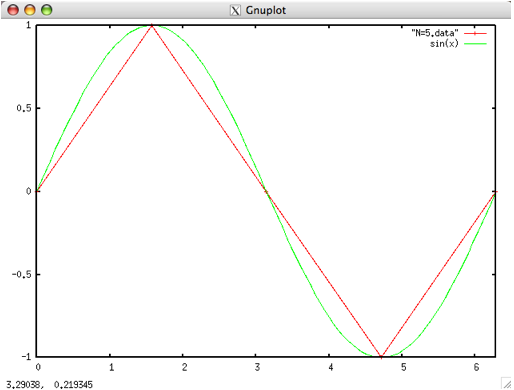
緑色で書かれたグラフが描きたいグラフ (y = sin(x) )です.
赤色が描こうとしている折れ線です.
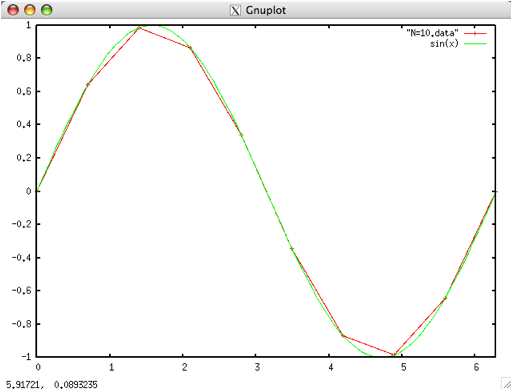
N=5 の場合は上図のようになります(赤線).
これでは、まったく y = sin(x) のグラフには見えません.
つづいて、プログラムを変更しNを10にして同様に N=10.data を作成しグラフを描いてみます.
曲線っぽくみえてきました.
N=50 の場合.見た目はほぼ y=sin(x) のグラフに見えます.
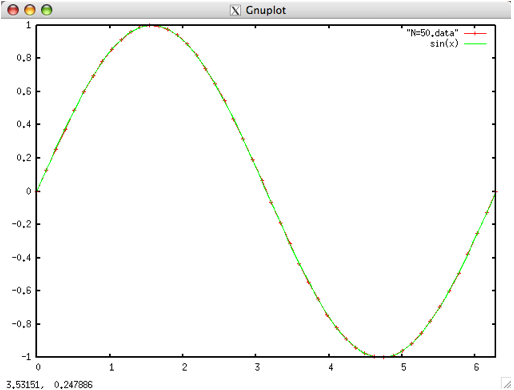
さて,曲線を折れ線で近似することができました.
実は gnuplot も内部で同じことをやっています.
標準状態で100本の折れ線で描いています.
例えば.
set sample 10
plot [0:2*pi] sin(x)
等とすると、その指定された数(ここでは 10本)の折線で曲線を描きます.(試してみてください.)
先のプログラム例では、 説明の為,少々冗長なプログラムとなっていました.
実際には以下のプログラムでも同様の結果が得られます.
各人確認してください.
#include <stdio.h>
#include <math.h>
/* 定数の定義 */
#define N (5)
#define PI (3.1415926)
#define L (2*PI)
int main()
{
int i;
double dx;
/* dx を求める */
dx = L/(N - 1);
/* 結果を画面に表示 */
for(i = 0; i < N; i++)
{
printf("%lf %lf\n", i*dx, sin(i*dx));
}
return 0;
}
(gnuplotについては、webで検索すると、詳しい使いかたが載っているHPが幾つか見付かります。また専門書を置いている書店にもいくつか解説書があると思います。それらを参考に、いろいろいじってみて下さい。)
課題1
gnup-1.cを改造して、cos(x) – cos(1.1 x)のデータを出力するプログラムを作成し、その計算結果をファイルunari_dataに出力せよ。
ただし、出力するxの範囲は[0:150]とする。
表示範囲が広いので、Nは大きめ(1000程度)にとる必要があるので注意。
そして、gnuplotを用いて、
gnuplot > plot ‘unari-data’ w l
としたときに、周期20πの「うなり」が見えることを確認すること。
データファイルを用いずにgnuplot単体でも、cos(x)-cos(1.1 x)は描画可能。
gnuplot > plot cos(x) – cos(1.1*x)
とすればいい。だが、set sample で値を大きく設定しておかないと間違った結果がでるので注意。
(データファイルの作り方は、「データファイルの作成」を参照のこと)
課題2
gnup-1.cを改造して、正三角形、正方形、正五角形、正六角形を描いてください.(N を適度に変化させて)
(数値データのファイルへの書き出し方は、前述の「データファイルの作成」を参照)
(付け足し)gnuplot 内で
gnuplot> set size square
gnuplot> plot [-4:4][-4:4] ‘(データファイル名)’ with lines
とすると、縦軸、横軸の縮尺が同じグラフが描けます.(試してみて下さい.)
課題2.5
x(t)、y(t)は次のように定義されているとする。
x(t) = cos(t),
y1(t) = sin(a*t)
y2(t) = sin((a+0.02)*t)
実数aの入力をキーボードから受けつけ、tを0から300まで、動かしたときのt、x(t),y1(t),y2(t)を出力するプログラムを作成せよ。
(このとき、「aの値を入力してください。」とprintfしようとしても、dataファイルにすべて収納されてしまい画面には一切表示されないので、今回は、このような入力を促す文章の必要はない)
(x,y1), (x,y2)を同時に描画して、違いを確認してみよ。(a=1.0,1.5, 2.0などで確認すること)
ただし、出力されるデータはt=0から0.01毎に
0.00 x(0.00)の数値 y1(0.00)の数値 y2(0.00)の数値
0.01 x(0.01)の数値 y1(0.01)の数値 y2(0.01)の数値
0.02 x(0.02)の数値 y1(0.02)の数値 y2(0.02)の数値
…
と出力されるものとする。
(各数値の間には、スペースが一つはいる。ここでが、小数点以下の桁数が二桁になるように表示してあるが、何桁であってもかまわない。)
また必ずgnuplotで可視化し、xy平面でどのような図が描けているか確認すること。
課題3
x(t)、y(t)は次のように定義されているとする。
x(t) = (1.5+sin(n*t/2))*cos(t),
y(t) = (1.5+sin(n*t/2))*sin(t)
正の整数nの入力を促し、tを0から12.5まで、動かしたときのt、x(t)、y(t)を出力するプログラムを作成せよ。
ただし、出力されるデータはt=0から0.01毎に
0.00 x(0.00)の数値 y(0.00)の数値
0.01 x(0.01)の数値 y(0.01)の数値
0.02 x(0.02)の数値 y(0.02)の数値
…
と出力されるものとする。
(各数値の間には、スペースが一つはいる。
ここでが、小数点以下の桁数が二桁になるように表示してあるが、何桁であってもかまわない。)
課題4
以下の様な、6個の独立した(線等で繋がっていない)直径1の円が、正六角形状に並んでいる絵を描くプログラムを作成し、gnuplotで描画してください.
円一つにつき50個程度の点(N=50)を使い、例えばデータファイルを en6-data とし
plot ‘en6-data’ w l
としたときに、以下と同様の絵が描かれること。
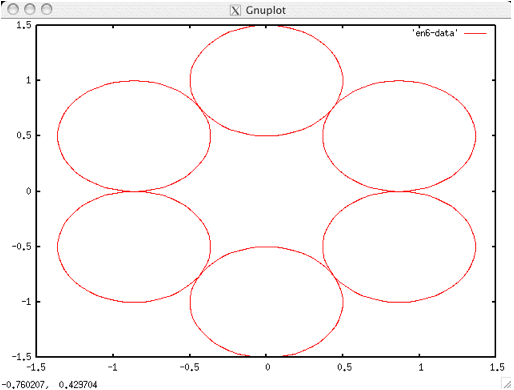
(ヒント)変数は円の中心座標、円周の各点の座標、およびそれぞれの位相。
また下記の例のように、改行コマンド printf(“\n”) をうまく使ってデータファイルに空白行をつくる
データに空白行を作る例
例えば次のように printf(“\n”)(何も書かずに改行のみする)を使うと、下記のような空白行のあるデータが作成できます。
#include <stdio.h>
int main()
{
int i,j;
/** 3回繰り返し **/
for(i=0; i<3; i++)
{
/** 0 1 2 を表示させる部分 **/
for(j=0; j<3; j++)
{
printf("%d\n", j);
}
/** j についての繰り返し処理後に何も書かずに改行(空白行をつくる) **/
printf("\n");
}
return 0;
}
これをコンパイルして実行すると
0
1
2
0
1
2
0
1
2
と、空行付きで表示されます。課題2ではこれを応用してください。
今日学んだ事
- gnuplot とCプログラムでグラフ、図形を描画しました。