計算数学演習第１０回

gnuplotを用いたデータのグラフ描画

今日の演習

今日は以下の内容で演習を行います．

  • Cプログラムとgnuplotを使った、グラフ、図形の描写 のつづき

今日の目標

gnuplot で計算結果を可視化する。


Gnuplotのあれこれ（軸，ラベル等）

・タイトル(title)、軸の名前(xlabel , ylabel)、各データの名前

下に載せているグラフには、タイトルと軸、各曲線に名前がついてます。
このように名前をつけるには、次のようにします。

gnuplot を起動

set title "Sin waves"
set xlabel "x"
set ylabel "F(x)"

　ここでは一行目でグラフの名前を、２行目で横軸(x軸)の名前を、３行目で縦軸(y軸)の名前を設定しています。

　これで、図全体のタイトルと、各軸の名前の設定が終わりました。

plot [0:2*pi][-1.5:1.5] sin(x) title "wave 1", sin(2*x) title "wave 2", sin(3*x) title "wave 3”

　描写の際、最後に title “名前” と付けることで、各曲線に自由な名前が付けられます。
これはもちろんデータファイルを描画する際にも有効です。

実際に入力して結果を確かめてください。

・関数の定義

また、gnuplotでは自分で関数を定義することも可能です。

f(x,a) = sin(a*x)
plot f(x,1), f(x,2)

という使い方も可能なので、各自調べてみてください。

・ 再描画

replot

と入力すると。一番最後に入力した描画（今回の範囲ではplotの文）の命令文が実行されます。


データの値をそのまま出力するのではなく、さらに処理を行った上で出力する方法

“第二列の値に0.5を加えたもの”や”第二列の値を2倍したもの”を描画したいとき

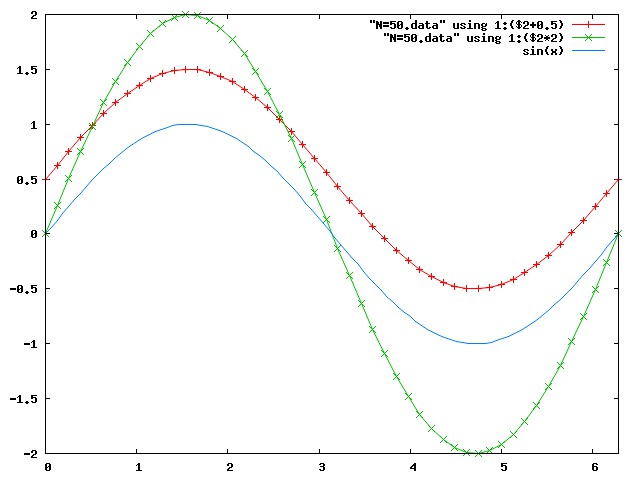
plot [0:2*pi] "N=50.data" using 1:($2+0.5) w lp, "N=50.data" using 1:($2*2) w lp, sin(x)

と打ち込むと、下図のような結果が出ます。
これと同様の方法でusing 1:($3-$2)で”第三列から第二列を引いたもの”を描画することも可能です。

対数表示
指数的に大きくなる値は，そのまま描画するより
縦軸を対数座標にしたほうがわかりやすいことがある．

exp(x)

を縦軸のみ対数座標で描画するためには，

set logscale y
plot exp(x)

とする．

元のｙ座標に戻したい場合は，

unset logscale

で元に戻せる．

グラフの印刷の仕方

gnuplot で作成したグラフを印刷したい場合には，ps ファイルに保存すると便利です．
その場合の手順は次のようになります．
（例えば sin(x) のグラフが描かれた ps ファイル 「sin_graph.eps」 を作成する場合.）

gnuplot 起動中に

set term postscript eps
set output "sin_graph.eps"
plot sin(x)
set term x11
set output

(もし、gnuplot自体を終了していいのなら、set term x11の代わりにquitと入力してくれてかまいません)

これによって，「sin_graph.eps」 というファイルができあがります．
ここでは、一行目で出力形式の変更、２行目で出力先のファイル名の指定、をしています.
ファイル名や plot の部分を適宜変更して下さい.
（set output … と plot … の間で set title … 等 (上の「gnuplot 付け足し」参照.) をすると、タイトル、軸の名前付きの ps ファイルができます．）

作成した psファイルをファイルブラウザでダブルクリックすると、適当なpsファイルビューアが起動するので、それから印刷してください．（最寄りのプリンターから印刷されます.）
ちなみに ps ファイルとは PostScriptファイルの略です．
PostScriptとはプリンタの制御言語で，プリンタに絵を描かせる命令の集まりです．

色付きで保存したい場合：

最初の文を

set term postscript enhanced color eps

と入力

数列の収束の様子をみる.その１

課題１

次の数列X_{n}=(1+\frac{1}{n})^nを、n: 1 ～ 200 程度まで求めるプログラムを作成し、nとX_n の関係を gnuplot で可視化せよ.
（n\rightarrow \inftyでX_n \rightarrow e（ネイピア数）ですね。収束の様子を確認してください。）

課題２

次の等式（Leibniz-Gregoryの等式）

    \[\frac{\pi}{4} = 1 - \frac{1}{3} +\frac{1}{5}-\frac{1}{7}+ \cdots +\frac{(-1)^n}{2n-1}+ \cdots\]

を利用して、\piの近似値を求めるプログラムを作成せよ。
右辺の項の数と\piの近似値 との関係を gnuplot で可視化せよ.
（ n: 1 ～ 1000 程度までで、おおよその傾向を見てください。）

数列の収束の様子をみる.その２（漸化式）

課題３

次の漸化式で表される数列X_nを求めるプログラムを作成し、n (0 ~ 100)とX_nの関係を gnuplot で可視化せよ。

    \[X_{n+1} = 1 + \frac{1}{X_n}\]

    \[X_0=1\]

（ i \rightarrow \inftyでX_iはいわゆる黄金比に収束します。収束の様子を確認してください。）

課題４ (Logistic map)

次の漸化式で表される数列 (0<X_i<1) を求めるプログラムを作成し、iとX_iの関係を gnuplot で可視化せよ.

    \[X_{i+1} = A*X_{i}*(1.0-X_{i})\]

A < 1 ならX_i \rightarrow 0(i \rightarrow \infty)となるのは、すぐ分ると思います.

A = 0.5, 2.0, 3.2, 3.5, 3.9 等（A : 0 ～ 4）それぞれの場合について、初期値X_0を0.3, 0.6, 0.61 等（0 ～ 1）と変化させ、実行、描画して見比べてください.　X_{0}, \dots, X_{49}を描画せよ．Aの値により，一つの値に収束する場合，二つの値の間を振動する場合，など様々な振る舞いを示すことを確認せよ．

課題５　Logistic mapの分岐ダイアグラム

課題４の式で、A=2.0, 2.001,2.002,..,3.999,4.0の場合についてX_{1000}, \dots, X_{1050}を計算し，
一列目をAの値，二列目をそのAにおけるX_nとして，以下のような形式で出力するプログラムを作成せよ．
ただし，どのAにおいてもX_0=0.1であるものとする，
出力例：
2.000 X_{1000}
..
2.000 X_{1050}
2.001 X_{1000}
…
2.001 X_{1050}
2.002 X_{1000}
…
4.000 X_{1050}
（合計 2001*51行のデータ）
このデータをもとにgnuplotでグラフを作成してみること．
散布図( データファイルをdiagram.txtとした場合，plot “diagram.txt” w d　と書くと綺麗に見える．）


課題６ (n周期解)

課題４の漸化式で与えられるx_iで8周期解，3周期解，６周期解に収束するものは存在するだろうか．
存在するなら，それぞれの場合に対応するaの値を見つけ，横軸i　縦軸x_iのグラフを描画してみよ．
（初期値x_0は0.1とする．）
ただし，ここでいうn周期解とはx_i=x_{i+n}を満たす解である，
（a=3.2のときはiが大きいときこの性質を持つ解に収束するので，２周期解に収束するといえる．）

課題７　カオス入門（発展問題）

課題４の式で，A=3.9

一列目　i

二列目　X_i（X_0=0.6のとき)

三列目　X_i（X_0=0.600001のとき）

となる数値データを出力し，

横軸が一列目の値，

縦軸が二列目と三列目の差の絶対値を出力せよ．

(gnuplot で絶対値を計算するには， abs()を使う）

また，縦軸を対数表示にすることにより，二つの値の離れ方を確認してみよ．

（興味のある人は，初期値鋭敏性というキーワードを調べてみてください）

課題おまけ

次の関数を描画してみてください.

plot [-7:7][-2:2] x-(x**3)/3/2/1+(x**5)/5/4/3/2/1-(x**7)/7/6/5/4/3/2/1+(x**9)/9/8/7/6/5/4/3/2/1-(x**11)/11/10/9/8/7/6/5/4/3/2/1+(x**13)/13/12/11/10/9/8/7/6/5/4/3/2/1, sin(x)

(長いですが、行を変えずに続けて打ち込んで下さい.) これはsin(x)のTaylor展開です. ちょっと長いですが、展開項数を変つつ、sin(x)とその多項式展開とを比べてみてください.

今日学んだ事

  • gnuplot とCプログラムでグラフ、図形を描画しました。