オイラー法2
今日の演習
- 2階常微分方程式の数値解法(オイラー法)
- n階常微分方程式についても連立1階常微分方程式に帰着できること知る
オイラー法による2階常微分方程式解法
つづいて、2階常微分方程式をオイラー法を用いて解いてもらいます.次の問題を考えます.
(1) 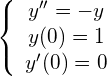
これは単振動を記述する2階の常微分方程式です.
ただし簡単の為、時間![]() での微分を
での微分を![]() を用いてあらわしています.
を用いてあらわしています.
2階の常微分方程式は次のように連立の1階の常微分方程式に帰着できます.
![]() ,
, ![]() とおくと、(1)式は
とおくと、(1)式は
(2) 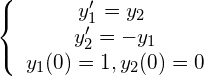
となります.
こうなれば先程と同様、オイラー法を用いて解を求めることができます.
もう少し一般的な書き方をすれば
![Rendered by QuickLaTeX.com \[ \left\{ \begin{array} $y_1' = f_1(t, y_1, y_2)$ \\ y_2' = f_2(t, y_1, y_2) \end{array} \right. \]](https://home.hiroshima-u.ac.jp/~mshira/wp/wp-content/ql-cache/quicklatex.com-295a834ba91e694603ab13ed4490acb4_l3.png)
![]() および
および![]() は,それぞれ関数で(2)式の場合には
は,それぞれ関数で(2)式の場合には![]() が第一式の右辺、
が第一式の右辺、![]() が第二式の右辺となります.
が第二式の右辺となります.
今回は![]() ,
,![]() という形になります.
という形になります.
アルゴリズムは次のようになります.
ただし、T を解を求める時刻の上限とし、N を時間刻み数、h = T/(N-1) を時間刻み幅とします.
変数は y1, y2 として、a1, a2 を初期値とします.
オイラー法による2階常微分方程式のアルゴリズム
・変数の宣言
T, h, a1, a2, y1, y2, y1_new, y2_new, t(時刻) 及び 関数 f1, f2 は実数型(floatまたはdouble)
N, j は整数型(int)
T,N,h を定める
y1 = a1, y2 = a2
初期時刻0と初期値a1, a2を画面に表示(printf関数)
j = 0,1,2,....,N-1の順に
t = j*h
y1_new = y1 + h*f1(t, y1, y2)
y2_new = y2 + h*f2(t, y1, y2)
y1 = y1_new
y2 = y2_new
一定間隔毎t+h, y1_new, y2_new を画面に表示(printf関数)
を繰り返す
各ステップで, y1_new, y2_new が両方求まってから y1 = y1_new, y2 = y2_new と値を更新するようにします.
ここの順序が変わってくると, y1 と y2 で時間がずれてしまうので, 正確な計算になりません.
課題1
(2) をオイラー法で解き、グラフを描け.グラフは横軸が t であり、縦軸を y(t) とせよ.
また、時間刻み幅 h を変えたときに結果がどのようにかわるか観察せよ.
時刻 0≦t≦20の範囲において、h = 0.0001, 0.001, 0.01, 0.1それぞれの場合(時間刻み数 N を調整.)について、微分解 ![]() とどの程度あっているか調べよ.
とどの程度あっているか調べよ.
色々な h に対する計算結果は次のようになる.
この結果から、h は十分小さい値でないとまずいことが分かります.
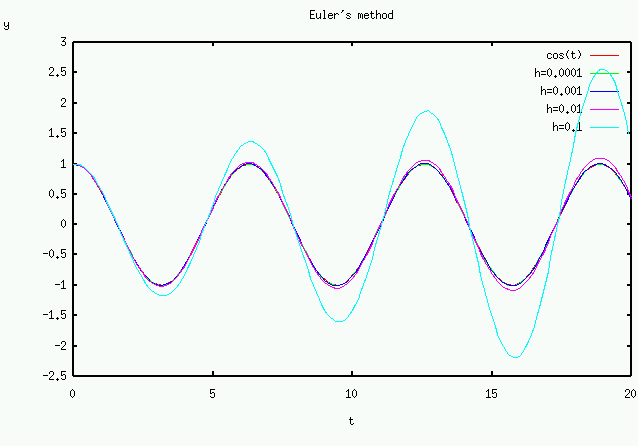
この課題の結果から分かるように、オイラー法では h を十分小さくとらないと本当の解をうまく近似できません.
h を小さく取るということは、計算時間が多くかかることを意味します.
そこでより高精度で大きな h でもうまく解を近似できるような解法が求められます.
そのような要求に応えるルンゲ・クッタ法があります(次回に説明します)。
課題2
次の微分方程式
(3) 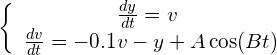
を、初期値y=1, v=0,A=2.0のもと数値的に解き B = 0,0.5,1,2 の場合の y の時間変化を調べて下さい(時刻の上限を少し大きめにして下さい.).
また、y と v の関係(gnuplot で横軸を y, 縦軸を v として)も plot してみて下さい.
これは摩擦抵抗のあるバネ振動子に、周期的な外力を加えたもので、強制振動系と呼ばれます.
様々な機械の「振動」が、このような方程式を応用しながら解析されています.
レポート課題
下の図のように、壁に一端を固定されたバネの他端におもりがつけられている状況を考えます.
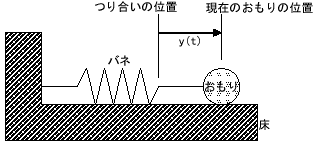
このおもりを少しだけ右に引っ張ってから手をはなす.
おもりの中心の時刻 t におけるつり合いの位置からのずれを y(t) とします.
また、時刻 0 でのおもりの位置を y(0)=1、おもりの速度を y'(0)=0 とすると、
課題1と全く同じ、つぎの単振動の問題となります.
(4) 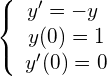
これではおもりに働く力はバネの復元力のみで、ある意味非現実的です.
今回は復元力以外におもりの速度![]() に比例する抵抗が働く場合を考えましょう.
に比例する抵抗が働く場合を考えましょう.
(おもりと床との間の摩擦力のようなものをイメージ).
改良されたモデルは次のようになります
(![]() の項が新たに加わったもので、摩擦のようなものをあらわしている).
の項が新たに加わったもので、摩擦のようなものをあらわしている).
(5) 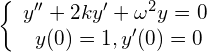
ここで![]() はそれぞれ抵抗力、復元力の強さを表す正の定数です.
はそれぞれ抵抗力、復元力の強さを表す正の定数です.
課題は、(5)式の問題を連立1階常微分方程式に変換し、オイラー法を用いて解くプログラムrep20190122.cを作成してください.
ただし,![]() , h=0.0001とし,出力はt, y(t), y'(t)の3成分で,
, h=0.0001とし,出力はt, y(t), y'(t)の3成分で,
0.0 y(0.0) y'(0.0)
0.01 y(0.01) y'(0.01)
0.02 y(0.02) y'(0.02)
…
49.99 y(49.99) y'(49.99)
50.0 y(50.0) y'(50.0)
というふうに,tは0.01刻みで出力するようにしてください.
(ヒント:100回に1回出力するので,%を使うと良いでしょう)
kの値について:y(t)のグラフが下図のようになるkの値を見つけ,そのkの値を使ってプログラムを作成してください.
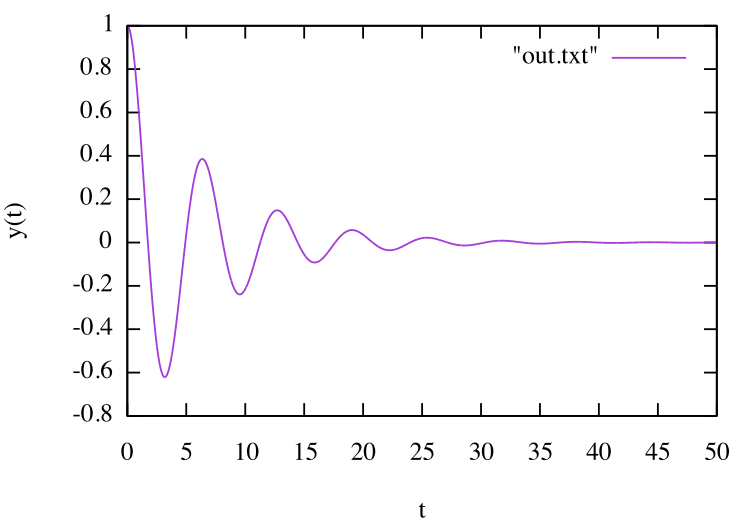
n階常微分方程式のオイラー法
ここまでに,2階常微分方程式は2変数1階常微分方程式へと変換し,1変数1階常微分方程式のアルゴリズムと同様にオイラー法で数値計算できることを学びました。
この変換方法は簡単に一般化できて,n階微分されている変数に対してn-1階微分を新たな変数と置き換えることで,その変数の1階微分としてn階微分されている変数を置き換えていけば全ての高階微分を1階微分で表現できます。
結果として,n変数の1階微分方程式へと変換することができます。
例えば,次の様な一般的な場合を考えます。
(6) ![]()
このn階常微分方程式に対して,![]() とすると,
とすると,
(7) 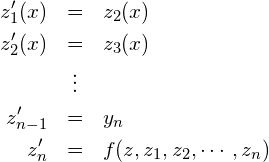
となりn変数1階常微分方程式とできます。