今日の演習
今日は以下の内容で演習を行います.
- 2階常微分方程式の数値解法(オイラー法)
 階常微分方程式の数値解法(オイラー法)
階常微分方程式の数値解法(オイラー法)
1階常微分方程式の数値解法
前回,簡単な1階常微分方程式をオイラー法にて解いてもらいました.
いくつか講義で出てきた問題をあげておきます.
オイラー法で解いてみて,解をグラフとして表示してみてください.
初期値やパラメータを適当にきめて,いくつかシミュレーションしてみてください.
(1) 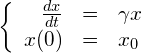
(2) 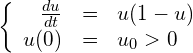
オイラー法による2階常微分方程式解法
2階常微分方程式もオイラー法を用いて解くことができます。
次の問題を考えて行きましょう。
(3) 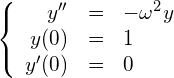
講義の説明の通り(下の枠中)、これは単振動を記述する2階の常微分方程式です。
ただし簡単の為、時間![]() での微分を ‘ を用いてあらわしています。
での微分を ‘ を用いてあらわしています。
バネ定数![]() のバネの一端を固定し、他端に質量
のバネの一端を固定し、他端に質量![]() のおもりをつけた状況を考える。
のおもりをつけた状況を考える。
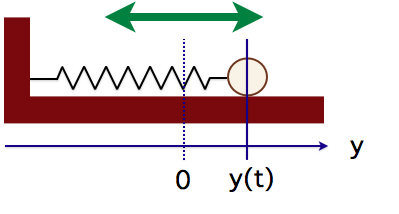
このおもりを少しだけ右に引っ張ってから手をはなす。
おもりの中心の時刻![]() におけるつり合いの位置からのずれを
におけるつり合いの位置からのずれを![]() とすると。
とすると。
![]() が満たす微分方程式は
が満たす微分方程式は
(4) ![]()
ただし、
(5) ![]()
とした。
2階の常微分方程式は次のように連立の1階の常微分方程式に帰着できます。
![]() とおくと、式(3)は、
とおくと、式(3)は、
(6) 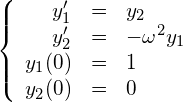
となります。
この形になれば、前回紹介したオイラー法を用いて解を求めることができます。
アルゴリズムは次のようになります。
但し、![]() を解を求める時間の上限、
を解を求める時間の上限、![]() を時間刻み幅、
を時間刻み幅、![]() を時間刻み数とします。
を時間刻み数とします。
また、変数は![]() として、
として、![]() を初期値とします。
を初期値とします。
また、![]() および
および ![]() はそれぞれ関数で式(6)の場合には
はそれぞれ関数で式(6)の場合には![]() が第一式の右辺、
が第一式の右辺、![]() が第二式の右辺となります。
が第二式の右辺となります。
オイラー法のアルゴリズム
解を求める時刻の上限を T とし、適当な自然数 N を定めて h=T/N とする。
T, h, a1, a2, y1, y2, y1_new, y2_new, t 及び 関数 f1, f2 は実数型(double)
N, j は整数型(int)
T,N,h を定める
y1 = a1, y2 = a2
t = 0 でのグラフの描画 (g_move 関数)
j = 0,1,2,….,N-1の順に
t = j*h
y1_new = y1 + h*f1(t, y1, y2)
y2_new = y2 + h*f2(t, y1, y2)
y1 = y1_new
y2 = y2_new
一定間隔毎にグラフを描画 (g_plot 関数)
を繰り返す
f1(t,y1,y2), f2(t, y1,y2) は関数として定義するとよい.
課題1
式(3)を解析的に解け。
課題2
![]() として式(6) をオイラー法で解き、グラフを描け。グラフは横軸が
として式(6) をオイラー法で解き、グラフを描け。グラフは横軸が![]() であり、縦軸を
であり、縦軸を![]() とせよ。
とせよ。
また、時間刻み幅![]() を変えたときに結果がどのようにかわるか観察せよ。
を変えたときに結果がどのようにかわるか観察せよ。
0≦t≦20の範囲において、h=0.0001,0.001, 0.01, 0.1それぞれの場合について、解析解とどの程度あっているか各自調べよ。
色々な h に対する計算結果は次のようになる(緑はh=0.1、青はh=0.01、ピンクはh=0.001、黄色はh=0.0001のときの結果。赤は解析解のグラフ)。
この結果から、h は十分小さい値でないとまずいことがよく分かる。
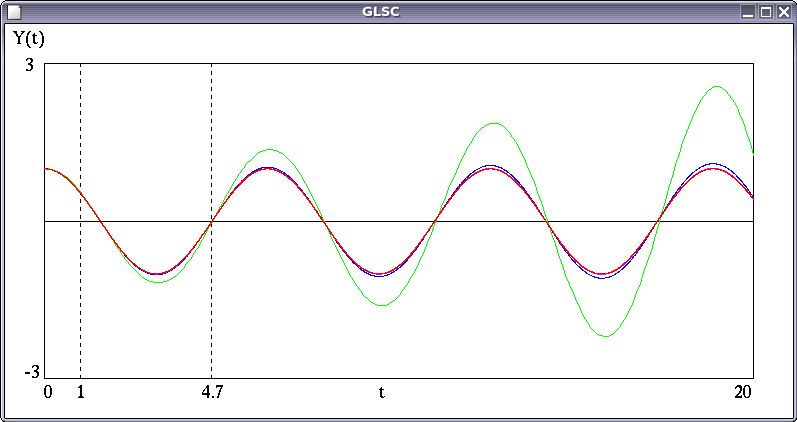
| オ イラー法では h を十分小さくとらないと本当の解をうまく近似できません。h を小さく取るということは、計算時間が多くかかることを意味します。そこでより高精度で大きな h でもうまく解を近似できるような解法が求められます。そのような要求に応える解法としては、ルンゲ・クッタ法があります。 |
課題3
課題2のプログラムを用いて、
(7) ![]()
を計算せよ。結果は、横軸を![]() 、縦軸を
、縦軸を![]() とするグラフで確認すること。
とするグラフで確認すること。
この![]() は
は![]() のときの、バネの力学エネルギーに対応する。
のときの、バネの力学エネルギーに対応する。
課題4
先程単振動を考察しましたが, 実際のバネではバネの復元力以外におもりの速度![]() に比例する抵抗が働く。
に比例する抵抗が働く。
その抵抗を考慮すると、式(3)ではなく次の式になる。(![]() の項が新たに加わった。)
の項が新たに加わった。)
(8) 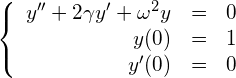
ここで![]() は抵抗力の強さを表す正の定数です。
は抵抗力の強さを表す正の定数です。
式(8)の問題を連立1階常微分方程式に変換し、オイラー法を用いて解き、GLSCをつかって、下のように「左端から線の繋がった赤い質点が振動する」動画を作成してください。
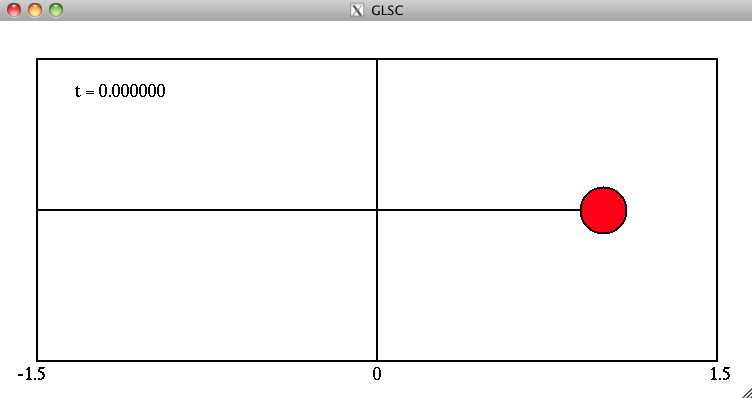
ただし、![]() とし、時間の刻み幅
とし、時間の刻み幅![]() は、0.01とします。
は、0.01とします。
ます。また、左上の”t= ..”は現在の![]() を表示している。
を表示している。
デモプログラムでは、時間の刻み幅は![]() として、
として、![]() まで計算しています。
まで計算しています。
また、提出するプログラムでは、アニメーションの描画を![]() が
が![]() 動く毎におこなうようにしてください。(ヒント1: “%”をつかったif文)
動く毎におこなうようにしてください。(ヒント1: “%”をつかったif文)
これは、無駄にプログラムの実行時間が長くなるのを防ぐためです。
以下、アドバイス等:
“t=”の部分のアニメーションのさせ方:カウントダウンを行うサンプルプログラムを参考にしてください。
質点の赤い領域:g_area_color(G_RED)とg_circleで塗りつぶしにG_YES。
課題5
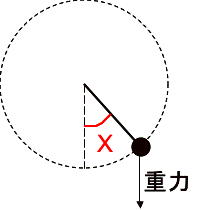
下図のような重力下で棒の長さ![]() が一定の振り子運動について、振り子の角度(ラジアン)を
が一定の振り子運動について、振り子の角度(ラジアン)を![]() とすると
とすると![]() は
は
(9) ![]()
という運動方程式を満たす(![]() は重力加速度、摩擦は無視しています)。
は重力加速度、摩擦は無視しています)。
![]() として、この方程式を適当な初期条件、
として、この方程式を適当な初期条件、![]() でシミュレーションし、GLSC を用いた振り子の動画を作成せよ。
でシミュレーションし、GLSC を用いた振り子の動画を作成せよ。
今回の課題は、オイラー法では十分に小さい![]() を用いないと計算結果がすぐにずれてしまいますが, 練習としてやってみてください.
を用いないと計算結果がすぐにずれてしまいますが, 練習としてやってみてください.
次回, オイラー法より計算精度の高いルンゲ・クッタ法を紹介しますが, そのときに比較してみてください.
課題6
課題4の振り子が2つ相互作用する場合を考える.
例えば, 2つの振り子の角度を![]() とすると、
とすると、![]() が
が
(10) 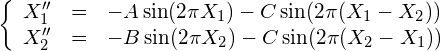
という運動方程式を満たすとする。
この方程式を適当な ![]() と初期条件、
と初期条件、![]() でシミュレーションし、GLSC を用いた振り子のアニメーションを作成せよ.
でシミュレーションし、GLSC を用いた振り子のアニメーションを作成せよ.
また振り子の数をもっと多くした場合も考察せよ.