第3回
今週は先週の続きを行います。
各自続きから始めるようにしてください。
直線の描画
g_move 関数とg_plot 関数を用いると直線を描くことができます。
g_move 関数で直線の始点を指定し、g_plot 関数で直線の終点を指定します。
また、g_line_color 関数で、直線の色を指定でき、g_line_width 関数で直線の幅を指定できます(それぞれマニュアル参照)。(0418-0.c)
#include <glsc.h>
#include <stdio.h>
int main()
{
g_init("GRAPH", 100.0, 100.0);
g_device(G_DISP);
g_def_scale(1, -1.0, 1.0, -1.0, 1.0, 10.0, 10.0, 80.0, 80.0);
g_sel_scale(1);
g_area_color(G_BLUE);
g_line_color(G_BLUE);
g_circle(0.0, 0.0, 0.5, G_YES, G_YES);
g_line_color(G_YELLOW);
g_line_width(3);
g_move(-1.0, -1.0);
g_plot(1.0, 1.0);
g_line_color(G_BLACK);
g_line_width(1);
g_move(-1.0, 1.0);
g_plot(1.0, -1.0);
g_sleep(G_STOP);
g_term();
return 0;
}
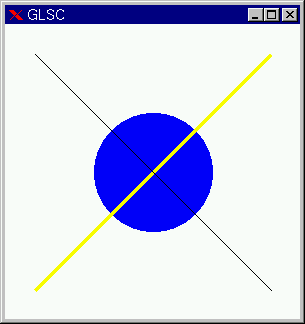
g_plot を連続してプログラム中に書くと、連続した直線を描く事ができます。
直前のプログラムの2つめの g_move を消去した次のプログラムでは、次のような結果となります(実際に2つめの g_move 関数を消去して試してみよ)。
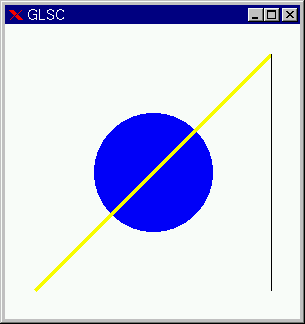
つまり、直前の g_plot 関数で指定された座標を始点とする直線が引かれます。
y = sin(x) のグラフの描画
これから、GLSCを使って![]() のグラフを描きます。
のグラフを描きます。
実際には![]() のグラフは滑らかな曲線ですが、コンピュータではそのような滑らかな曲線を直接は扱えませんので折れ線で近似します。
のグラフは滑らかな曲線ですが、コンピュータではそのような滑らかな曲線を直接は扱えませんので折れ線で近似します。
つまり、変数![]() は、実際には連続的に変化するものですが、とびとびの値を使います。
は、実際には連続的に変化するものですが、とびとびの値を使います。
後の例で見るように、とびとびとはいえ、十分に細かく取れば、折れ線で曲線をうまく近似することができます。
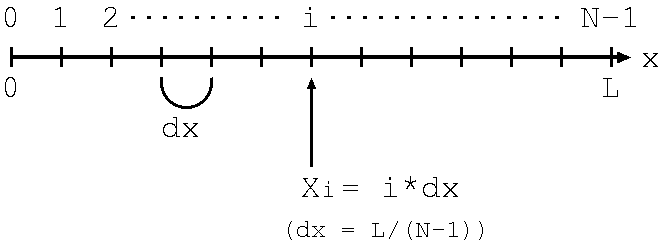
図のように![]() 区間を
区間を![]() 等分して、その等分した小区間の幅を
等分して、その等分した小区間の幅を![]() とします。
とします。
![]() 等分すると図のように
等分すると図のように![]() 個の区切りが現れますが、それらに
個の区切りが現れますが、それらに![]() と番号をつけることにします。
と番号をつけることにします。
また、 ![]() を分割数、
を分割数、 ![]() を分割幅と呼びます。このとき、
を分割幅と呼びます。このとき、
![]()
の部分についてそれぞれ![]() を計算し、それらを折れ線で結ぶことを考えます。
を計算し、それらを折れ線で結ぶことを考えます。
C言語風に書けば
X[i] = dx*i;
Y[i] = sin(X[i]);
をそれぞれ求め、(X[0], Y[0]), (X[1],Y[1]), …., (X[N-1], Y[N-1]) を結ぶ折れ線を描くことになります。
これをプログラムにすると次のようになります。(上記の説明にあわせるためにかなり無駄なことをしています。)
ファイル名を 0418-1.c として打ち込み、実行してみてください。
注意: 数学関数(sin, cos, tan 等)を使う場合には #include <math.h> が必要となります。
#include <glsc.h>
#include <stdio.h>
/* 次の文は数学関数を使う場合に必要 */
#include <math.h>
/* 定数の定義 */
#define N (5)
#define PI (3.1415926)
#define L (2*PI)
int main()
{
int i;
double X[N], Y[N], dx;
/* dx を求める */
dx = L/(N - 1);
/* GLSCの初期化および仮想座標系の定義 */
g_init("GRAPH", 200.0, 100.0);
g_device(G_DISP);
g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
/* 外枠の描画 */
g_sel_scale(1);
g_area_color(G_WHITE);
g_line_color(G_BLACK);
g_line_width(2);
g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
g_move(0.0, 0.0);
g_plot(L, 0.0);
/* X[i] を求める */
for(i = 0; i < N; i++)
{
X[i] = i*dx;
}
/* Y[i] を求める */
for(i = 0; i < N; i++)
{
Y[i] = sin(X[i]);
}
/* 折れ線の種類を設定 */
g_line_color(G_RED);
g_line_type(G_LINE_SOLID);
g_line_width(2);
/* 折れ線を描く */
g_move(X[0], Y[0]);
for(i = 1; i < N; i++)
{
g_plot(X[i], Y[i]);
}
g_sleep(G_STOP);
g_term();
return 0;
}
上記プログラムに、グラフの左端右端等の情報を書き入れたプログラムの出力を使って、![]() とグラフの関係を見てみましょう。
とグラフの関係を見てみましょう。
青色の破線で書かれたグラフが描きたいグラフ (![]() )です(とはいっても、もちろんこれも
)です(とはいっても、もちろんこれも![]() の折れ線です)。赤色の実線が描こうとしている折れ線です。
の折れ線です)。赤色の実線が描こうとしている折れ線です。
![]() の場合は次のようになります(赤線)。これでは、まったく
の場合は次のようになります(赤線)。これでは、まったく![]() のグラフには見えません。
のグラフには見えません。
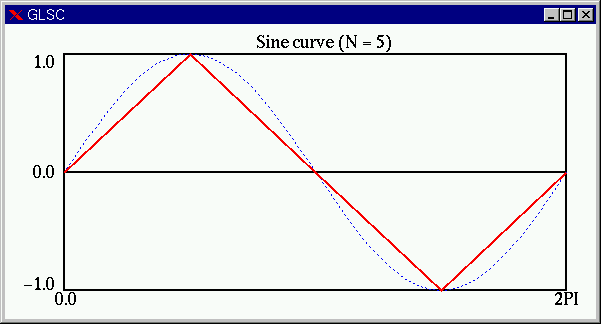
つづいて、![]() の場合(赤線)。曲線っぽくみえてきました。
の場合(赤線)。曲線っぽくみえてきました。
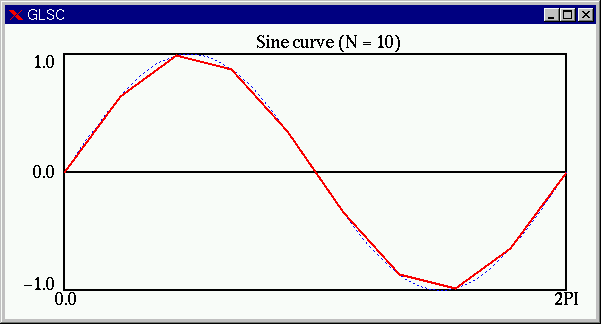
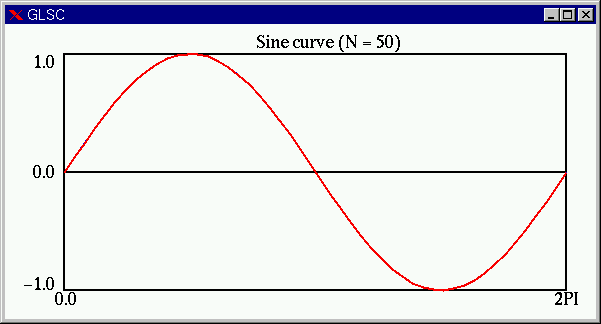
![]() の場合(赤線)。見た目はほぼ
の場合(赤線)。見た目はほぼ![]() のグラフに見えます。
のグラフに見えます。
課題2
上のサンプルプログラム(0418-1.c)を表示例のように表示するプログラムに変更せよ。
(グラフの左端等の表示と![]() のグラフを重ねて表示するように変更)
のグラフを重ねて表示するように変更)
ヒント: Y[N] とは別に Y0[100] という配列を作って、それぞれを異なる線種で描く。また、文字列の描画(その2)で説明した手法を用いてタイトル部分を書くと良い。(注意:g_text 関数の最初の2つの引数(座標は)標準座標系での値になります.)
課題3
![]() のグラフを
のグラフを![]() の範囲で描け。滑らかに見えるように、適度に
の範囲で描け。滑らかに見えるように、適度に![]() を調整すること. また、適度な大きさの「丸」を使った点描画でのグラフも描け.
を調整すること. また、適度な大きさの「丸」を使った点描画でのグラフも描け.
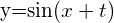 のグラフのアニメーション
のグラフのアニメーション
すでに、アニメーションの作り方を知っているので簡単です。ただし、いま![]() は時間として扱いますが、当然連続量として扱うことができないので、
は時間として扱いますが、当然連続量として扱うことができないので、![]() 同様とびとびの値として扱います。先ほどの
同様とびとびの値として扱います。先ほどの![]() と同様に考え、
と同様に考え、![]() の範囲を
の範囲を![]() として、それを
として、それを![]() 等分します。その小区間の幅を
等分します。その小区間の幅を![]() として(つまり、
として(つまり、![]() )、
)、
![]()
とすることにより、![]() を止めるごとに Y[i] = sin(Xi + Tk) のグラフを描くことを繰り返せば、アニメーションとなります。次のサンプルプログラムを 0418-2.c として打ち込み実行してみてください。これまでのアニメーションプログラムと仕組みが同じであることに気づくことが重要です。
を止めるごとに Y[i] = sin(Xi + Tk) のグラフを描くことを繰り返せば、アニメーションとなります。次のサンプルプログラムを 0418-2.c として打ち込み実行してみてください。これまでのアニメーションプログラムと仕組みが同じであることに気づくことが重要です。
課題4
上のアニメーションのプログラムで![]() を 5 にするとどうなるか?やってみよ。(好きな方法で構いません.)
を 5 にするとどうなるか?やってみよ。(好きな方法で構いません.)
課題5
課題3のプログラムにグラフの左端等の情報を表示する部分を追加せよ。
課題6
![]() のアニメーションを作成せよ。
のアニメーションを作成せよ。
課題7
![]() のアニメーションを作成せよ。
のアニメーションを作成せよ。