第4回(2016年4月20日)
今日の演習
y = sin(x) のグラフの描画
これから、GLSCを使って![]() のグラフを描きます。
のグラフを描きます。
実際には![]() のグラフは滑らかな曲線ですが、コンピュータではそのような滑らかな曲線を直接は扱えませんので折れ線で近似します。
のグラフは滑らかな曲線ですが、コンピュータではそのような滑らかな曲線を直接は扱えませんので折れ線で近似します。
つまり、変数![]() は、実際には連続的に変化するものですが、とびとびの値を使います。
は、実際には連続的に変化するものですが、とびとびの値を使います。
後の例で見るように、とびとびとはいえ、十分に細かく取れば、折れ線で曲線をうまく近似することができます。
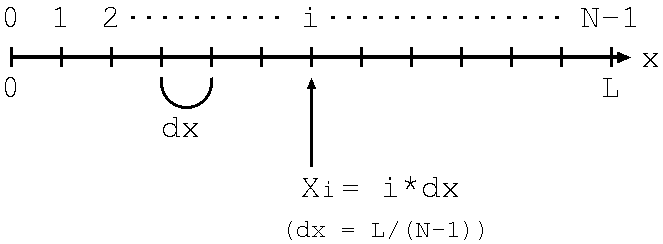
図のように![]() 区間を
区間を![]() 等分して、その等分した小区間の幅を
等分して、その等分した小区間の幅を![]() とします。
とします。
![]() 等分すると図のように
等分すると図のように![]() 個の区切りが現れますが、それらに
個の区切りが現れますが、それらに![]() と番号をつけることにします。
と番号をつけることにします。
また、![]() を分割数、
を分割数、![]() を分割幅と呼びます。このとき、
を分割幅と呼びます。このとき、
![]()
の部分についてそれぞれ![]() を計算し、それらを折れ線で結ぶことを考えます。
を計算し、それらを折れ線で結ぶことを考えます。
C言語風に書けば、
X[i] = dx*i;
Y[i] = sin(X[i]);
をそれぞれ求め、(X[0], Y[0]), (X[1],Y[1]), …., (X[N-1], Y[N-1]) を結ぶ折れ線を描くことになります。
これをプログラムにすると次のようになります。(上記の説明にあわせるためにかなり無駄なことをしています。)
ファイル名を 0420-1.c として打ち込み、実行してみてください。
注意: 数学関数(sin, cos, tan 等)を使う場合には #include <math.h> が必要となります。
#include <glsc.h>
#include <stdio.h>
/* 次の文は数学関数を使う場合に必要 */
#include <math.h>
/* 定数の定義 */
#define N (5)
#define PI (3.1415926)
#define L (2*PI)
int main()
{
int i;
double X[N], Y[N], dx;
/* dx を求める */
dx = L/(N - 1);
/* GLSCの初期化および仮想座標系の定義 */
g_init("GRAPH", 200.0, 100.0);
g_device(G_DISP);
g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
/* 外枠の描画 */
g_sel_scale(1);
g_area_color(G_WHITE);
g_line_color(G_BLACK);
g_line_width(2);
g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
g_move(0.0, 0.0);
g_plot(L, 0.0);
/* X[i] を求める */
for(i = 0; i < N; i++)
{
X[i] = i*dx;
}
/* Y[i] を求める */
for(i = 0; i < N; i++)
{
Y[i] = sin(X[i]);
}
/* 折れ線の種類を設定 */
g_line_color(G_RED);
g_line_type(G_LINE_SOLID);
g_line_width(2);
/* 折れ線を描く */
g_move(X[0], Y[0]);
for(i = 1; i < N; i++)
{
g_plot(X[i], Y[i]);
}
g_sleep(G_STOP);
g_term();
return 0;
}
上記プログラムに、グラフの左端右端等の情報を書き入れたプログラムの出力を使って、![]() とグラフの関係を見てみましょう。
とグラフの関係を見てみましょう。
青色の破線で書かれたグラフが描きたいグラフ![]() )です(とはいっても、もちろんこれも
)です(とはいっても、もちろんこれも![]() の折れ線です)。
の折れ線です)。
赤色の実線が描こうとしている折れ線です。
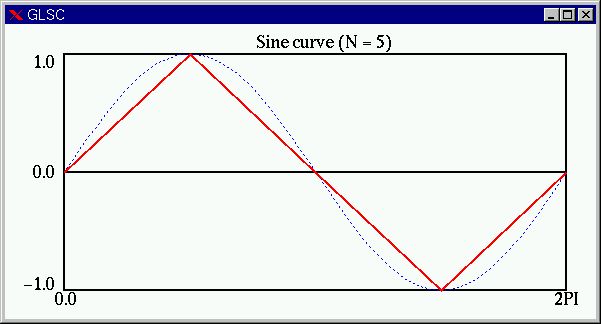
![]() の場合は次のようになります(赤線)。
の場合は次のようになります(赤線)。
これでは、まったく![]() のグラフには見えません。
のグラフには見えません。
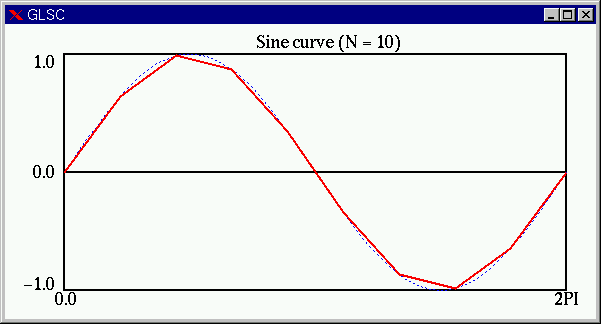
つづいて、![]() の場合(赤線)。曲線っぽくみえてきました。
の場合(赤線)。曲線っぽくみえてきました。
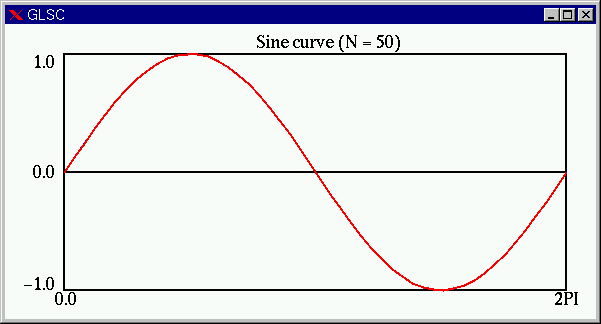
![]() の場合(赤線)。見た目はほぼ
の場合(赤線)。見た目はほぼ![]() のグラフに見えます。
のグラフに見えます。
課題1
上のサンプルプログラム(0421-1.c)を表示例のように表示するプログラムに変更せよ。
(グラフの左端等の表示と![]() のグラフを重ねて表示するように変更)
のグラフを重ねて表示するように変更)
ヒント: Y[N] とは別に Y0[100] という配列を作って、それぞれを異なる線種で描く。また、文字列の描画(その2)で説明した手法を用いてタイトル部分を書くと良い。(注意:g_text 関数の最初の2つの引数(座標は)標準座標系での値になります.)
課題2
![]() のグラフを
のグラフを![]() の範囲で描け。滑らかに見えるように、適度に
の範囲で描け。滑らかに見えるように、適度に![]() を調整すること. また、適度な大きさの「丸」を使った点描画でのグラフも描け.
を調整すること. また、適度な大きさの「丸」を使った点描画でのグラフも描け.
y = sin(x + t) のグラフのアニメーション
すでに、アニメーションの作り方を知っているので簡単です。ただし、いま![]() は時間として扱いますが、当然連続量として扱うことができないので、
は時間として扱いますが、当然連続量として扱うことができないので、![]() 同様とびとびの値として扱います。先ほどの
同様とびとびの値として扱います。先ほどの![]() と同様に考え、
と同様に考え、![]() の範囲を [0, T] として、それを K-1 等分します。その小区間の幅を
の範囲を [0, T] として、それを K-1 等分します。その小区間の幅を![]() として(つまり、 dt = T/(K-1))、
として(つまり、 dt = T/(K-1))、
Tk = dt*k
とすることにより、 Tk を止めるごとに Y[i] = sin(Xi + Tk) のグラフを描くことを繰り返せば、アニメーションとなります。次のサンプルプログラムを 0428-2.c として打ち込み実行してみてください。前々回のアニメーションプログラムと仕組みが同じであることに気づくことが重要です。(先のプログラムにはあったX[N]の配列は不要なのでなくしています.(先のプログラムでも実際にはX[N] の配列は不要でした))。
#include <glsc.h>
#include <stdio.h>
#include <math.h>
/* 定数の定義 */
#define N (50)
#define K (100)
#define PI (3.1415926)
#define L (2*PI)
#define T (10.0)
int main()
{
int i, k;
double Y[N], dx;
double dt;
/* dx, dt を求める */
dx = L/(N - 1);
dt = T/(K - 1);
g_init("GRAPH", 200.0, 100.0);
g_device(G_DISP);
/* 仮想座標系の定義 */
g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
g_sel_scale(1);
/* 毎時間繰り返し */
for(k = 0; k < K; k++)
{
/* グラフ等を消去 */
g_cls();
/* 外枠の描画 (毎時刻グラフの消去してから描き直す) */
g_area_color(G_WHITE);
g_line_color(G_BLACK);
g_line_width(2);
g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
g_move(0.0, 0.0);
g_plot(L, 0.0);
/* Y[i] を求める */
for(i = 0; i < N; i++)
{
Y[i] = sin(i*dx + k*dt);
}
/* 折れ線の種類*/
g_line_color(G_RED);
g_line_type(G_LINE_SOLID);
g_line_width(1);
/* 描画の開始点 */
g_move(0.0, Y[0]);
/* 描画(曲線をつなぐ) */
for(i = 0; i < N; i++)
{
g_plot(i*dx, Y[i]);
}
g_sleep(0.05);
}
g_sleep(G_STOP);
g_term();
return 0;
}
上記プログラムでは, i について Y[i] を一度全部求めてから, 再び i について Y[i] を描く, というように2度手間になってますが, このように計算しながら描く事も出来ます. また, 点描画もできます.
課題3
上のアニメーションのプログラムで![]() を 5 にするとどうなるか?やってみよ。
を 5 にするとどうなるか?やってみよ。
(好きな方法で構いません.)
課題4
課題2のプログラムにグラフの左端等の情報を表示する部分を追加せよ。
課題5
![]() のアニメーションを作成せよ。
のアニメーションを作成せよ。
課題6
![]() のアニメーションを作成せよ。
のアニメーションを作成せよ。
簡単な常微分方程式とその解のグラフ化
今日は、計算数理Aの講義に出てきた次の常微分方程式を用いて演習を進めます。この方程式は、講義で詳しく説明されたと思いますが、例えば放射性同位体の崩壊を記述するモデル方程式として導出されます。講義で紹介があったように、例えば放射性炭素による年代測定にはこういった微分方程式が役立ちます。![]() を時刻
を時刻![]() における放射性同位体の原子数とすると下記のような微分方程式が得られることは講義で見たとおりです。
における放射性同位体の原子数とすると下記のような微分方程式が得られることは講義で見たとおりです。
(P) 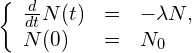
さて、この微分方程式は簡単に解けて、解は次のようになることも講義で見ました。
(S) ![]()
今日の目標は、解(S)をグラフとして表示するGLSCプログラムを作成することです。パラメータ![]() および
および![]() を与えれば、(S)のグラフをかけるはずです。実は前回の内容で
を与えれば、(S)のグラフをかけるはずです。実は前回の内容で![]() のグラフを描いてもらいましたが、そこで注意したようにコンピュータを用いてこのようなグラフを描く場合には折れ線近似で描く必要があります。前回の
のグラフを描いてもらいましたが、そこで注意したようにコンピュータを用いてこのようなグラフを描く場合には折れ線近似で描く必要があります。前回の![]() を描く方法を記述した部分にしたがって、(S)のグラフを描いてください。
を描く方法を記述した部分にしたがって、(S)のグラフを描いてください。
課題7
GLSCを用いて、![]() のグラフを描け。(0428-1.c, 0428-2.c 等を参考にせよ.)
のグラフを描け。(0428-1.c, 0428-2.c 等を参考にせよ.)
ただし、![]() とする。
とする。
例えば次のようになる。(この例では、0≦t≦10 を 100等分している。つまり時間刻み幅を dt と書くことにすると、 dt = 10/100 = 0.1 である。曲線を100本の直線のつながりである折れ線で近似するのである。)
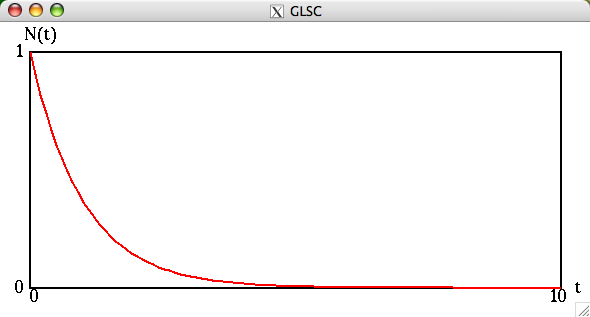
課題8
![]() となる
となる![]() を求めよ。((S)を用いて具体的に求めよ)
を求めよ。((S)を用いて具体的に求めよ)
答え: ![]() (約 0.693)
(約 0.693)
課題9
課題7で作成したプログラムを用いて課題8のτを近似的に次のような手法で求めたい。そのようなプログラムを作成せよ。
方法
![]() の値を(S)を用いて飛び飛びの
の値を(S)を用いて飛び飛びの![]() の値
の値![]() (ただし
(ただし![]() は時間刻み幅)について求めるのであるが、(S)と課題6のグラフから明らかなように
は時間刻み幅)について求めるのであるが、(S)と課題6のグラフから明らかなように![]() は単調減少関数である。であるから、
は単調減少関数である。であるから、
![]()
となる![]() があるであろう。このとき、
があるであろう。このとき、![]() を
を![]() の近似値
の近似値![]() とする。
とする。
![]() を100等分して上記方法にて
を100等分して上記方法にて![]() の近似値を求め、課題7で求めた値との差(誤差と呼ぶ)
の近似値を求め、課題7で求めた値との差(誤差と呼ぶ)
![]()
を求めよ。
注意:当然ながら刻み数を100から1000に増やせばより正確な値が求まる。
参考:
課題8、課題9(後で出てきます)の方法は、![]() が具体的に与えられていない場合 (例えば実測データなど)にも有効なので、実用的です。
が具体的に与えられていない場合 (例えば実測データなど)にも有効なので、実用的です。
課題10
課題9の方法ではあまり良い精度で近似値を求めることができない。
次の方法でより精度良く近似値をもとめることを考える。
![]()
なる![]() を求め、2点
を求め、2点![]() を結ぶ直線を考える。
を結ぶ直線を考える。
その直線と![]() の直線の交点の
の直線の交点の![]() の値
の値![]() をもって、
をもって、![]() の近似値をする。
の近似値をする。
(このような手法を線形補間と呼ぶ。)
![]() を100等分して上記方法にて
を100等分して上記方法にて![]() の近似値を求め、課題2で求めた値との差
の近似値を求め、課題2で求めた値との差
![]()
を求めよ。課題9の結果よりも良いだろうか?
注意:
課題9の方法でも刻み数を増やせばより正確な値が求まるのであるが、課題10の補間を使えば、あまり多くない刻み数でも正確な近似値が得られることを実感してほしい。
課題11
課題10において刻み数100で近似値を求めた場合の誤差と同程度に小さい誤差とするためには課題9において刻み数をどの程度にしなければならないか。実験してみよ。
常微分方程式の数値解法
次のような常微分方程式の初期値問題を、オイラー法と呼ばれる方法を用いて数値的に解き、GLSCを用いて結果をグラフにしてもらいます。次の問題を考えます。
(1) 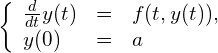
求めたいのは、![]() の範囲の
の範囲の![]() であり、関数
であり、関数![]() および定数
および定数![]() は与えられているとします。また、
は与えられているとします。また、![]() の値は
の値は![]() が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
コンピューターでは数値を離散的に(とびとびに)しか扱うことができません。そこで、(1)式をコンピューターで扱えるようにする必要があります。(1)をコンピュータで解く方法には色々とありますが、この演習では代表的なオイラー法を用います。その前に、準備として差分商について説明します。
差分商
![]() を
を![]() の関数としたとき、
の関数としたとき、![]() の
の![]() における微分係数は
における微分係数は
(2) ![]()
で定義されます。ここで、定義中の極限操作を取り払い、![]() を有限にとどめた
を有限にとどめた
(3) ![]()
を考えると、![]() を十分小さな正の実数ととれば、(3)式は(2)式の近似となっていると考えられます。
を十分小さな正の実数ととれば、(3)式は(2)式の近似となっていると考えられます。
この![]() のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、(3)式の右辺のような量を差分商といいます。いまの場合は1階微分係数を近似する1階差分商です。
のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、(3)式の右辺のような量を差分商といいます。いまの場合は1階微分係数を近似する1階差分商です。
では、このような差分商を用いて(1)式を離散化してみましょう。まず、(1)式の第一式の微分係数を上記の差分商で置き換えてみます。
(4) ![]()
ただし、![]() は正の数とします。(4)式と(1)式の第一式は異なる方程式なので、(1)式の第一式の解
は正の数とします。(4)式と(1)式の第一式は異なる方程式なので、(1)式の第一式の解![]() は一般に(4)式を満たしません。
は一般に(4)式を満たしません。
そこで、混乱を防ぐために(4)式の![]() を
を![]() と書き換えましょう。
と書き換えましょう。
(5) ![]()
(5)式のように差分を含む方程式を差分方程式といいます。
次に、(1)式の![]() を
を![]() に置き換えた初期条件
に置き換えた初期条件
(6) ![]()
の下で(5)式を解くことを考えます。(5)式は、
(7) ![]()
と変形できるので、t = 0 を代入すると、
(8) ![]()
となり、Y(0) から直ちに Y(h) が求まります。同様にして(7)式を繰り返し用いると、
(9) 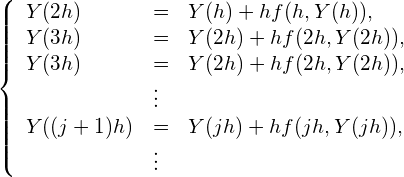
というように、![]() とすると
とすると![]() を
を![]() から計算できることがわかります。
から計算できることがわかります。
![]() をいったん決めると、
をいったん決めると、![]() 以外の時刻の
以外の時刻の![]() の値は(7)式からは求めることができません。
の値は(7)式からは求めることができません。
このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります。そのようなとびとびの時刻を格子点と呼びます。
![]() は格子点でのみ意味があるので、そのことを明示するために
は格子点でのみ意味があるので、そのことを明示するために![]() を
を![]() と書き換え、
と書き換え、![]() とすると、(5)式と初期条件は、
とすると、(5)式と初期条件は、
(10) 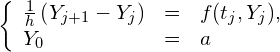
となり、結局(1)式の常微分方程式の初期値問題が、![]() に関する漸化式の問題(10)式に置き換えられました。この方法をオイラー法と呼びます。
に関する漸化式の問題(10)式に置き換えられました。この方法をオイラー法と呼びます。
オイラー法のアルゴリズム
オイラー法のアルゴリズムを以下に擬似コードで表す。
解を求める時刻の上限をTとし、適当な自然数Nを定めてh=T/Nとする。
T, h, a, Y, t 及び 関数 f は実数型(double)
N, j は整数型(int)
T, Nを設定
h = T/N
aを設定(入力する:printf関数+scanf関数)
Y = a
t = 0でのグラフの描画(g_move関数)
j = 0, 1, 2, ..., N-1の順に(for文)
t = j * h
Y = Y + h * f(t, Y)
一定時間毎にグラフを描画(g_plot関数)
以上をj=N-1まで繰り返す。