今日の演習
グローバル変数(全ての関数から読み書きできる変数)
関数内で宣言された変数は,基本的には「その関数の中だけで」用いられます.
先の例で,plus_one関数が,main関数の変数iを使って計算をしたではないかと思うかもしれませんが,
あれは「plus_one関数の中身が実行される前に変数numberにiの値が代入されただけ」であり,
plus_one関数は直接 変数iを見る事も値を変更することもできません.
plus_one関数内で iという変数を(宣言なしに)使ってしまったらエラーになります.
ですが,どの関数からでも自由に読み書きのできる変数というものが存在します.
そのような変数をグローバル変数と呼びます.
グローバル変数は関数の外で(関数より先に)宣言します.
宣言する位置さえ守れば,それだけでグローバル変数となります.
#include<stdio.h>
/*global変数の宣言*/
int global_i=0;
/* 関数の宣言(returnを使わない関数はvoidとする)*/
void plus_some(int number);
int main()
{
int local_i = 0;
plus_some(local_i);
printf("global_i = %d, local_i = %d\n",global_i,local_i);
plus_some(local_i);
printf("global_i = %d, local_i = %d\n",global_i,local_i);
return 0;
}
void plus_some(int number)
{
global_i += 100; /* global_i = globa_i + 100 の意味*/
number += 10;
}
実行してみると,
global_i = 100, local_i = 0 global_i = 200, local_i = 0
となり,グローバル変数の方のみ値が変更されているのがわかります.
グローバル変数として配列も宣言可能です.
このように,グローバル変数は大変便利なものなので,「いっそ全ての変数をグローバル変数にしてしまってもいいのではないか?」
と思うかもしれませんが,本演習ではそれを推奨しません.
必要最小限の変数をグローバル変数として用いてください.
無駄にグローバル変数を多く用いるとプログラムの可読性が悪くなるばかりか,バグを誘発する可能性があるので注意して用いてください.
課題1
関数をうまく使うことで,プログラムを読み易くすることができます.
次のプログラムは,放物線を描くプログラムです.
#include<stdio.h>
#include <glsc.h>
int main()
{
int i;
double x[11],y[11];
/* preparation*/
g_init("GRAPH", 200.0, 100.0);
g_device(G_DISP);
g_def_scale(1, -1.0, 1.0, 0.0, 1.0, 10.0, 10.0, 180.0, 90.0);
g_sel_scale(1);
/*determine_x_y */
for(i =0; i<11; i++)
{
x[i] = 0.2*i - 1.0;
y[i] = x[i]*x[i];
}
/*draw_graph*/
g_move(x[0], y[0]);
for(i = 1; i < 11; i++)
{
g_plot(x[i], y[i]);
}
g_sleep(G_STOP);
g_term();
}
グローバル変数と関数を用いて,メイン関数が次のようにシンプルな形で表せるようにソースコードを書き換えてください.
int main()
{
graph_preparation();
determine_x_y();
draw_graph();
g_sleep(G_STOP);
g_term();
return 0;
}
前回やったsin(x+t)のアニメーションのプログラムも,main関数をすっきりさせることができます.
#include <stdio.h>
#include <math.h>
#include <glsc.h>
/* 定数の定義 */
#define N (50)
#define K (100)
#define PI (3.1415926)
#define L (2*PI)
#define T (10.0)
/* プログラム中で変更されないので定数にしてしまったもの*/
#define dx (L/(N - 1))
#define dt (T/(K - 1))
/*global変数の宣言*/
float Y[N];
/*関数のプロトタイプ宣言*/
void graph_preparation();
void determine_y(int time_steps);
void draw_graph();
main()
{
int i, k;
/* windowサイズ,仮想座標系の設定*/
graph_preparation();
/* 毎時間繰り返し */
for(k = 0; k < K; k++)
{
/* グラフ等を消去 */
g_cls();
/* Y[i] を求める */
determine_y(k);
/*グラフの描画*/
draw_graph();
g_sleep(0.05);
}
g_sleep(G_STOP);
g_term();
}
void draw_graph()
{
int i; /*local変数 i の宣言*/
/* 外枠の描画 (毎時刻グラフの消去してから描き直す) */
g_area_color(G_WHITE);
g_line_color(G_BLACK);
g_line_width(2);
g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
g_move(0.0, 0.0);
g_plot(L, 0.0);
/* 折れ線の種類*/
g_line_color(G_RED);
g_line_type(G_LINE_SOLID);
g_line_width(1);
/* 描画の開始点 */
g_move(0.0, Y[0]);
/* 描画(曲線をつなぐ) */
for(i = 0; i < N; i++)
{
g_plot(i*dx, Y[i]);
}
}
void graph_preparation()
{
g_init("GRAPH", 200.0, 100.0);
g_device(G_DISP);
/* 仮想座標系の定義 */
g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
g_sel_scale(1);
}
void determine_y(int time_steps)
{
int i; /*local変数 i の宣言*/
for(i = 0; i < N; i++)
{
Y[i] = sin(i*dx + time_steps*dt);
}
}
常微分方程式の数値解法
今回は次のような常微分方程式の初期値問題を、オイラー法と呼ばれる方法を用いて数値的に解き、GLSCを用いて結果をグラフにしてもらいます。
オイラー法は計算数学演習で扱っていますが, おさらいをしておきます。 次の問題を考えます。
(1) 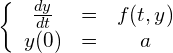
求めたいのは、![]() の範囲の
の範囲の![]() であり、関数
であり、関数![]() および定数
および定数![]() は与えられているとします。
は与えられているとします。
また、![]() の値は
の値は![]() が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
が与えられればいつでも計算できるものとします。(関数として定義するとよい。)
コンピューターでは数値を離散的に(とびとびに)しか扱うことができません。
そこで、(1)式をコンピューターで扱えるようにする必要があります。
(1)式をコンピュータで解く方法には色々とありますが、今回は代表的なものの一つであるオイラー法を用います。
その前に、準備として差分商について説明します。
差分商
![]() を
を![]() の関数としたとき、
の関数としたとき、![]() の
の![]() における微分係数は
における微分係数は
(2) ![]()
で定義されます。ここで、定義中の極限操作を取り払い、![]() を有限にとどめた
を有限にとどめた
(3) ![]()
を考えると、![]() を十分小さな正の実数ととれば、(3)式は(2)式の近似となっていると考えられます。
を十分小さな正の実数ととれば、(3)式は(2)式の近似となっていると考えられます。
この![]() のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、(3)式の右辺のような量を差分商といいます。
のように、関数のいくつかの点における値の差を用いてその関数の微分係数を近似することを差分近似といい、(3)式の右辺のような量を差分商といいます。
いまの場合は1階微分係数を近似する1階差分商です。
では、このような差分商を用いて(1)式を離散化してみましょう。
まず、(1)式の第一式の微分係数を上記の差分商で置き換えてみます。
(4) ![]()
ただし、![]() は正の数とします。
は正の数とします。
(4)式と(1)式の第一式は異なる方程式なので、(1)式の第一式の解 y(t) は一般に(4)式を満たしません。
そこで、混乱を防ぐために(4)式の![]() を
を![]() と書き換えましょう。
と書き換えましょう。
(5) ![]()
(??)式のように差分を含む方程式を差分方程式といいます。
次に、(1)式の![]() を
を![]() に置き換えた初期条件
に置き換えた初期条件
(6) ![]()
(7) ![]()
と変形できるので、![]() を代入すると、
を代入すると、
(8) ![]()
となり、![]() から直ちに
から直ちに![]() が求まります。同様にして(7)式を繰り返し用いると、
が求まります。同様にして(7)式を繰り返し用いると、
(9) 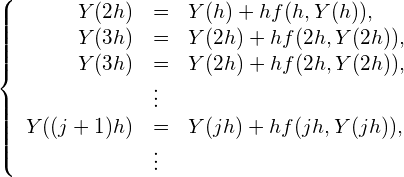
というように、![]() とすると
とすると![]() を
を![]() から計算できることがわかります。
から計算できることがわかります。
![]() をいったん決めると、
をいったん決めると、![]() 以外の時刻の
以外の時刻の![]() の値は(7)式からは求めることができません。
の値は(7)式からは求めることができません。
このように、差分方程式を解くと従属変数はとびとびの時刻で値が定まります。
そのようなとびとびの時刻を格子点と呼びます。
![]() は格子点でのみ意味があるので、そのことを明示するために
は格子点でのみ意味があるので、そのことを明示するために![]() を
を![]() と書き換え、
と書き換え、![]() とすると、(5)式と初期条件は、
とすると、(5)式と初期条件は、
(10) 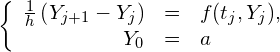
となり、結局(1)式の常微分方程式の初期値問題が、![]() に関する漸化式の問題(9)式に置き換えられました。この方法をオイラー法と呼びます。見やすいように(9)を書き直すと
に関する漸化式の問題(9)式に置き換えられました。この方法をオイラー法と呼びます。見やすいように(9)を書き直すと
(11) 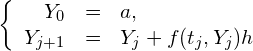
となります。
オイラー法のアルゴリズム1
解を求める時刻の上限を![]() とし、適当な自然数
とし、適当な自然数![]() を定めて
を定めて![]() とする。
とする。
T, h, a 及び 関数 f は実数型(float)
N, j は整数型(int)
Y[N+1], t[N+1] は実数型配列(float)
T, N, aを設定 (#define文で定数として定義すれば良い)
配列Y[N+1], t[N+1]を用意する
h = T/N (TおよびN双方が整数型でないか注意)
Y[0] = a (初期条件の設定)
t[0] = 0
j = 0, 1, 2, ..., N-1の順に(for文)
t[j+1] = j * h
Y[j+1] = Y[j] + h * f(t[j], Y[j])
以上をj=N-1まで繰り返す。
点(t[0], Y[0]), (t[1], Y[1]), ... , (t[N], Y[N]) を直線で結ぶことにより数値解をグラフとして描画 (g_move, g_plot関数)
f(t,Y) は関数(上で復習してます)として定義するとよい.
以下のアルゴリズム2では,数値解を求めながらグラフを描いています.
(アルゴリズム1では,数値解を全て求めた後グラフを描いている.)
オイラー法のアルゴリズム2
解を求める時刻の上限を T とし、適当な自然数 N を定めて h=T/N とする。
T, h, a, Y, Y_new, t 及び 関数 f は実数型(float)
N, j は整数型(int)
T, N, aを設定 (#define文で定数として定義すれば良い)
h = T/N
Y = a
t = 0
j = 0, 1, 2, ..., N-1の順に(for文)
t = j * h
Y_new = Y + h * f(t, Y)
一定間隔毎にグラフを描画(g_plot関数)
Y = Y_new(Yの値を更新)
以上をj=N-1まで繰り返す。
f(t,Y) は関数(上で復習してます)として定義するとよい.
(計算数学演習での「関数の定義」の解説とサンプルプログラムはこちらにあります.)
簡単な常微分方程式とその数値解のグラフ化
さて,実際にオイラー法をつかって常微分方程式を解いてみましょう.
今回も、計算数理Aの講義に出てきた次の常微分方程式を用いて演習を進めます。
(ただし![]() を
を![]() と書き換えた.上記アルゴリズム等の分割数
と書き換えた.上記アルゴリズム等の分割数![]() とまぎらわしいので.)
とまぎらわしいので.)
(P) 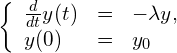
前回は,この微分方程式を解析的に解いて得られた解をグラフ化してもらいました。
今回は(P)式をオイラー法を用いて数値計算で解いて,得られた数値解をグラフ化してもらいます.
計算数学演習での「オイラー法の解説とサンプルプログラム」はこちらにあります. 参考にしてください.
アルゴリズム2の方が,少ない変数で計算を行っているのでスマートだといえます.
アルゴリズム1の方が解り易い人も多いでしょうから,アルゴリズム1を用いても良いです.
課題2
(P)をオイラー法で解き,得られた数値解をグラフとして表示するプログラムを作成せよ.ただし,
![]()
とする。例えば次のようになる。
(この例では、![]() を100等分している。つまり時間刻み幅を h と書くことにすると、 h = 10.0/100 = 0.1 である。)
を100等分している。つまり時間刻み幅を h と書くことにすると、 h = 10.0/100 = 0.1 である。)
(縦軸がN(t)となっているがy(t)と読み替えてください.)
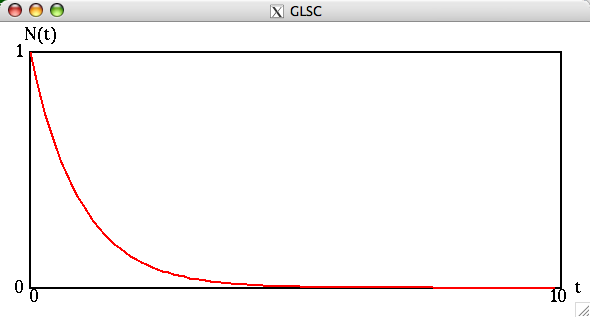
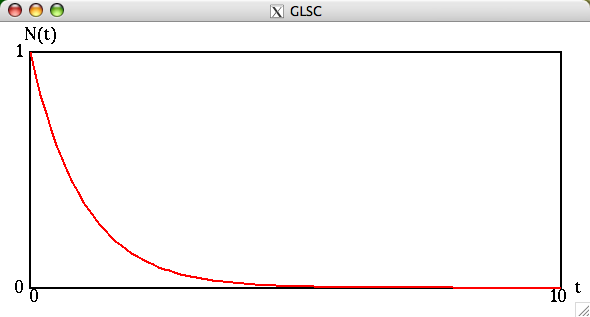
先週,解析的に求めた解をグラフとして表示したものは以下であるが,殆ど違いがない事に注意.
(課題3でみるが,微妙に異なっている)
課題3
前回解析的に求めた解(S)とオイラー法で求めた数値解を重ねて描くプログラムを作成せよ.
例えば,次のようになる.
この例では,解(S)を緑色で描き,数値解を赤色で描いている.
(この例では、0≦t≦10 を 100等分している)
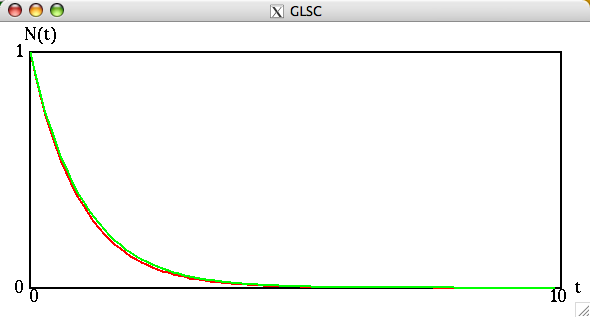
刻み幅を小さくすると両者の差は縮まる.(次の例では、0≦t≦10 を 300等分している)
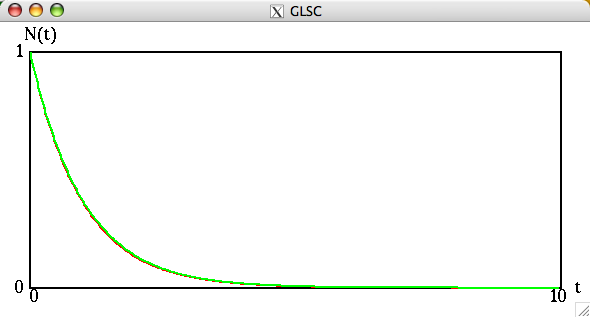
レポート課題
課題3で作成したプログラムを少し変更して,
「λの値の入力を促し,そのλの値における解析解とオイラー法で求めた数値解を重ねて表示する」
プログラムをrep20180425.cという名前で作成し,Bb9から提出して下さい.
初期値,x,yの表示範囲は課題3と同じでかまいません.
0≦t≦10 を 100等分とすること.数字や軸の名前が描いてあるかどうかも評価のポイントです.
関数を作ってmain関数をシンプルに(読み易く)記述しているものは高く評価します.
インデント(時下げ),コメントは必ず行うこと.
また,プログラムの最初の方にコメントとして学生番号と氏名は(最低限)必ず記述すること.
(/*bxxxxxx 氏名 */)
提出期限2018年4月27日(金)12時00分
課題4
次の常微分方程式の初期値問題をオイラー法を用いて解いて、t と y の関係を GLSC でグラフ化せよ.
(1) dy/dt = -y + sin(t), y(0) = 1 (時刻 0≦ t ≦20 の範囲を20000等分割、100ステップ毎に値を表示)
(2) dy/dt = y(5-y), y(0) = 1 (時刻 0≦ t ≦20 の範囲を20000等分割、50ステップ毎に値を表示)
(3) dy/dt = y – 2y3, y(0) = 0.1 もしくは y(0) = -0.1 (時刻 0≦ t ≦20 の範囲を20000等分割、100ステップ毎に値を表示)
自由課題(上記の課題が終わった人へ)
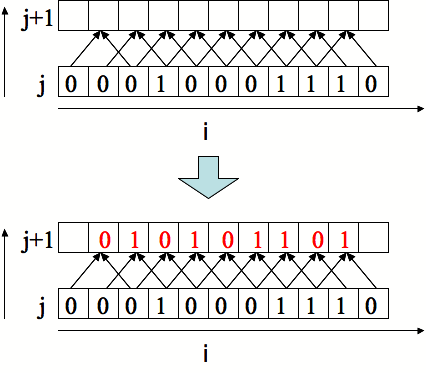
一次元セルオートマトンについて調べて,glscを用いて描いてみてください.
ただし,各xセル(値は0か1)は自分の値と両隣の値をもとに,次の時刻の自分の値を決定する物とします.
(セルの数は自由に設定してください)
例としてRule90と呼ばれるもの以下に示します.
(iがセルの番号で,jが時刻を表すと思ってください)
また時間発展のルールを変更したときに,どのようなことがおこるのか試してみてください.
(この枠組みだと時間発展のルールは256通りです.)