今日の演習
- 常微分方程式の数値解法 (ルンゲ・クッタ法)
- 課題色々
1階常微分方程式の数値解法(ルンゲ・クッタ法)
今回は次のような常微分方程式の初期値問題を、ルンゲ・クッタ法と呼ばれる方法を用いて数値的に解き、GLSCを用いて結果をグラフにしてもらいます。
(1) 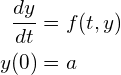
前回まではオイラー法を用いた数値解法の演習を行いました。
オイラー法は単純でそれはそれでよいのですが、実際の解に近い数値解を出すためには、時間刻み幅![]() をかなり小さくとらねばならないことが課題の結果からわかりました。
をかなり小さくとらねばならないことが課題の結果からわかりました。
そこで、より精度の高い解法が必要となりますが、今回はそのような解法として、ルンゲ・クッタ法を扱い、それを用いた数値解法の演習を行います。
ルンゲ・クッタ法の導出については、このページの最後を参照してください(詳細は参考書を参照してください)。
ルンゲ・クッタ法は次にしめすようなアルゴリズムで、オイラー法に比べれば多少複雑なものとなっています。
比較の為に両方のアルゴリズムを載せておきます(赤字の部分が異なります)。
よく比較してください。
| オイラー法 | ルンゲ・クッタ法 |
| T :解を求める時間の上限 h :時間刻み幅 N :時間刻み数 y:変数 a:初期値 y_new:実数型の変数 |
T :解を求める時間の上限 h :時間刻み幅 N :時間刻み数 y:変数 a:初期値 y_new, r_1, r_2, r_3, r_4 :実数型の変数 |
|
T,N,h を定める y_new = y + h*f(t,y)
y = y_new 一定間隔毎にグラフを描画 (g_plot 関数) f(t,y) は関数として定義するとよい. |
T,N,h を定める r_1 = f(t, y) y = y_new 一定間隔毎にグラフを描画 (g_plot 関数) f(t,y) は関数として定義するとよい. |
* オイラー法では, (とびとびの)時刻 t = jh での値 y から 次の(とびとびの)時刻 t = (j+1)h での値 y_new を直接計算しています。
本来、微分方程式では時刻は連続ですが、この場合は時刻 t = jh ~ (j+1)h の間の事は一切考慮されておらず、その分誤差が現れてきます。
* ルンゲ・クッタ法では, この t = jh ~ (j+1)h の間の情報を (r_1, ~ r_4 を使って ) いくらか取り入れる事で、よりよい近似計算が可能になっています。
勿論誤差は現れるのですが、オイラー法と比べて雲泥の差です。
以下の課題でそれを確認します。
課題1
上記のルンゲ・クッタ法を用いて次の問題を解き、ルンゲ・クッタ法がオイラー法と比べて、どの程度性能が良いか比べよ。
次の初期値問題を0≦t≦5の範囲でh=0.5とし、実際にオイラー法とルンゲ・クッタ法を用いて解け。
(2) 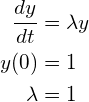
オイラー法を用いた解法プログラムを euler.c とし、同問題をルンゲ・クッタ法を用いて解くプログラムを rk.c とする。
解 y(t) = exp(t) とどの程度あっているか、一目でわかる GLSCプログラムにせよ。
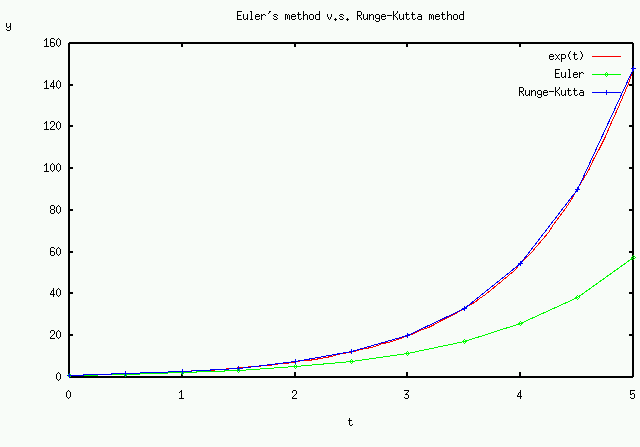
結果は大体次のようになります(このグラフは GLSC でかいたものではありませんが大体同じようなグラフをGLSCで描いてください)。
h=0.5とかなり粗く時間刻み幅をとっているにも関わらず、ルンゲ・ クッタ法は良く微分解を近似できていることがわかります。
それに比べてオイラー法は微分解から大きく離れてしまっています。これでは正しい計算とは言えな いでしょう。
2階(n階)常微分方程式の数値解法(ルンゲ・クッタ法)
前回の課題で扱った
(3) 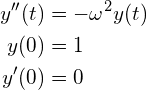
を![]() とおいて、次のように連立の1階の常微分方程式に帰着したもの
とおいて、次のように連立の1階の常微分方程式に帰着したもの
(4) 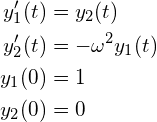
を再び考えます。
このような連立の常微分方程式をルンゲ・クッタ法を用いて解く場合のアルゴリズムを次に示します。
| 2階常微分方程式のルンゲ・クッタ法 |
| T :解を求める時間の上限 h :時間刻み幅 N :時間刻み数 Y1, Y2:変数 a1, a2:初期値 Y1_new, Y2_new, r1_1, r1_2, r1_3, r1_4, r2_1, r2_2, r2_3, r2_4 :実数型の変数 |
|
T,N,h を定める t = i*h r1_1 = f1(t, y1, y2) r1_2 = f1(t + h/2, y1 + (h/2)*r1_1, y2 + (h/2)*r2_1) r1_3 = f1(t + h/2, y1 + (h/2)*r1_2, y2 + (h/2)*r2_2) r1_4 = f1(t + h, y1 + h*r1_3, y2 + h*r2_3) y1_new = y1 + (h/6)*(r1_1 + 2*r1_2 + 2*r1_3 + r1_4) y1 = y1_new 一定間隔毎にグラフを描画 (g_plot 関数) を繰り返す f1(t,y1,y2), f2(t, y1,y2) は関数として定義するとよい. |
また、f1(t, y1, y2) および f2(t, y1, y2) はそれぞれ実数型の関数です。
(3)式の場合には f1 が第一式の右辺、 f2 が第二式の右辺となります。
(今回, ω = 1 とします.)
注意!:C言語の仕様の都合上,y0, y1, ynはグローバル変数の名前として好ましくない.
y_0, y_1, y_nや,Y0, Y1, Ynで代用すると良い.
課題2
ルンゲ・クッタ法を用いて、前回の課題4と同等のアニメーションを表示するプログラムを作成せよ。
γ=0、dt=0.1として、オイラー法との違いを確認すること。
課題3
次の連立微分方程式を適当な初期条件のもと、オイラー法かルンゲ・クッタ法で解いてください。
(5) 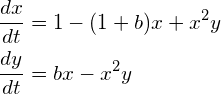
(1) b < 2 の場合
(2) b > 2 の場合
この方程式は、ブラッセレーター方程式といわれるもので、BZ反応と呼ばれる、時間的に化学成分の濃度が振動するような化学反応の振動をモデル化した方程式です。(BZ 反応とは何でしょう? http://www.chem.scphys.kyoto-u.ac.jp/nonnonWWW/kitahata/bz_1.html あたりが参考になります。)
課題4
次の連立微分方程式を適当な初期条件のもと、オイラー法かルンゲ・クッタ法で解いてください。
(6) 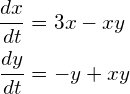
課題3の方程式同様、この方程式も振動解を見せますが、その特徴は少々違っております。
例えば初期条件を変えた場合に、これらの(課題5と課題6それぞれの)方程式系の解の振る舞いが、どのように変化していくか、見比べてください。
この方程式は、ロトカ・ボルテラ方程式といわれるもので、生態系内のある被食者と補食者の数 (x, y) 増減関係を簡単にモデル化した方程式です。
(各時刻、被食者はある割合(3x)で増えて、補食者に出会うと食べられ減る(-xy)。同様に捕食者は被食者 に出会うとそれを食べて増えて(xy)、ある割合で(-y)で寿命等で減っていく。)詳しい事は各自調べてください.
課題5
惑星の運動を考えます。万有引力の法則から2物体(質量はそれぞれ M,m)に働く力は
![]()
となります。![]() は2物体間の距離、
は2物体間の距離、![]() は万有引力定数で
は万有引力定数で
![]()
です。原点に太陽(質量 M)があり、惑星(質量 m)の位置を
![Rendered by QuickLaTeX.com \[\vec{r}(t) = \left( \begin{array}{c} r_1(t) \\ r_2(t) \\ r_3(t) \end{array} \right)\]](https://home.hiroshima-u.ac.jp/~mshira/wp/wp-content/ql-cache/quicklatex.com-2afcaab824aa67756781de50d64b8935_l3.png)
とします。惑星に働く力は
![Rendered by QuickLaTeX.com \[\vec{F} = - \frac{GMm}{|\vec{r}(t)|^2}\cdot \frac{\vec{r}(t)}{|\vec{r}(t)|} = -GMm\frac{\vec{r}(t)}{|\vec{r}(t)|^3}\]](https://home.hiroshima-u.ac.jp/~mshira/wp/wp-content/ql-cache/quicklatex.com-a0fb86e130122db78a28589f6f816673_l3.png)
となり、
![]()
より
![]()
とおくと、2階の常微分方程式の初期値問題
(7) 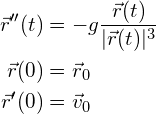
が得られます。これを1階の常微分方程式系に直し、数値計算にて解をもとめて下さい。
(まずは r3 を考えずに, r1 – r2 平面上の運動方程式として考えてもよろしいです.)
課題6
水星は太陽に非常に近く、その効果が公転に影響するため、その運動は以下のような方程式に従うようになる。
![Rendered by QuickLaTeX.com \[\frac{d^2\vec{r}(t)}{dt^2} = -g\frac{\vec{r}(t)}{|\vec{r}(t)|^3} + h\frac{\vec{r}(t)}{|\vec{r}(t)|^4}\]](https://home.hiroshima-u.ac.jp/~mshira/wp/wp-content/ql-cache/quicklatex.com-591a51a8c414b1e387d94e22defdb811_l3.png)
数値的に解をもとめてください。ただし、![]() とします。
とします。
ルンゲ・クッタ法について
簡単にルンゲ・クッタ法について説明します。演習で取り扱ったルンゲ・クッタ法は4段公式とよばれるものですが、ここでは簡単の為、2段公式を取り扱います。
次の常微分方程式の初期値問題の数値解を求めたいとしましょう。
(R1) 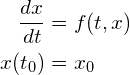
2段公式とは、![]() で(R1)の近似解
で(R1)の近似解![]() が求められたとして、時間ステップ幅
が求められたとして、時間ステップ幅![]() だけ進んだ
だけ進んだ![]() における値
における値![]() を次の形で計算する公式です。
を次の形で計算する公式です。
(R2) 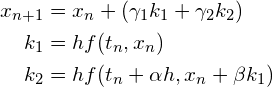
つまり、![]() から
から![]() へ進む1ステップにおいて方程式(R1)の第一式の右辺の
へ進む1ステップにおいて方程式(R1)の第一式の右辺の![]() を2回計算するので、2段公式と呼びます。
を2回計算するので、2段公式と呼びます。
この2段公式には、パラメータ![]() が含まれますが、これらは方程式(R1)の真の解
が含まれますが、これらは方程式(R1)の真の解![]() のテイラー展開
のテイラー展開
(R3) 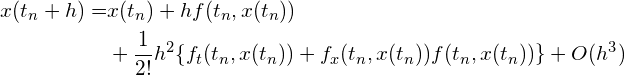
と(R2)式の第一式の同様の展開とが![]() のなるべく高い次数の項まで一致するように定めます。
のなるべく高い次数の項まで一致するように定めます。
つまり、![]() と仮定して(R2)式の
と仮定して(R2)式の![]() の式の右辺を
の式の右辺を![]() 周りでテイラー展開すると、
周りでテイラー展開すると、
(R4) 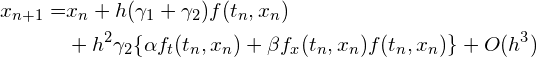
となります。
これと(R3)が![]() の項まで一致するように
の項まで一致するように
(R5) 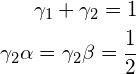
とおく。公式(R2)で定められる近似解のテイラー展開が![]() の2次の項まで真の解のテイラー展開に一致するという意味で、この公式を2次の公式と呼びます。
の2次の項まで真の解のテイラー展開に一致するという意味で、この公式を2次の公式と呼びます。
この公式は2段公式でもあるので、2段2次の公式とも呼ば れます。パラメータを定める方程式(R5)には自由度が2残っているのでその定め方によって色々な公式が導かれます。
(改良オイラー法、ホイン法、修正オイラー法など)
演習で用いた4段4次のルンゲ・クッタ法の公式も同様にして求めることが出来ます。