計算数理A演習第8回 – Masashi Shiraishi Homepage

今日の演習

振動いろいろ
（１）減衰振動
（２）強制振動
（３）自然界の振動

前回までに，常微分方程式はオイラー法とルンゲ・クッタ法の二種類の解法を用いて解く事ができました。
hが十分小さければルンゲ・クッタ法を用いて得た数値解（近似解）は，真の解に十分近いといえるでしょう。
今回からは，ルンゲ・クッタ法を常微分方程式を解く信頼できる方法として採用し，
具体的な問題を解き得られた解を見るだけでなく，現象に立ち返りその意味を再考してみましょう。
（ルンゲ・クッタ法になじめない方はオイラー法を用いるのでも構いません.）

減衰振動再考

減衰振動についてもう一度考えてみましょう。

課題１

下の図のように、壁に一端を固定されたバネの他端におもりがつけられている状況を考えます。

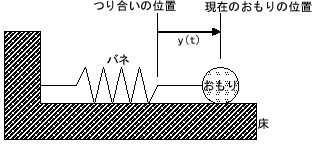
このおもりを少しだけ右に引っ張ってから手をはなす。
おもりの中心の時刻tにおけるつり合いの位置からのずれ（変位）を $y(t)$ とします。
また、時刻0でのおもりの位置を $y(0)=1$ 、おもりの速度を $y'(0)=0$ とすると次の単振動の問題となります。
（フックの法則を用いた）

(1) $\begin{equation*} \left\{ \begin{array}{rcl} y''(t) &=& -y(t) \\ y(0) &=& 1 \\ y'(0) &=& 0 \end{array} \right. \end{equation*}$

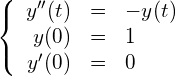
これではおもりに働く力はバネの復元力のみで、ある意味非現実的です。
今回は復元力以外におもりの速度y’に比例する抵抗が働く場合を考えましょう。
（講義ではダンパを加えた場合として説明されている）。
改良されたモデル方程式は次のようになります。

(2) $\begin{equation*} \left\{ \begin{array}{rcl} y''(t) + 2ky'(t)+\omega^2y(t) &=& 0 \\ y(0) &=& 1 \\ y'(0) &=& 0 \end{array} \right. \end{equation*}$

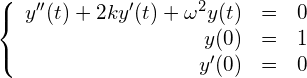
ここでk，ωはそれぞれ抵抗力、復元力の強さを表す正の定数です。
（２）式の問題を連立１階常微分方程式に変換し、ルンゲ・クッタ法（オイラー法）を用いて解き、GLSCを用いて解を可視化（グラフ）してください。
(前々回のレポートで提出されているプログラムを使い回してください。それを元に今日は現象を観察してもらいます)

以下の３通りについて，それぞれグラフを描いてください。
（例えば，ωをある値に固定して，kのみを変化させ，下記３通りを満たすようなkを選ぶとよい。３通りのグラフを色を変えて重ね描きするとよい。）

k<ωの場合：減衰振動
k>ωの場合：過減衰
k=ωの場合：臨界減衰

ところで，ドアは一種のバネ振り子＋ダンパ系と見る事ができる。
設計する際，ダンパの強さを臨界減衰になるよう設計するのが一番良いとされる。
なぜであろうか？考えてみてください。
（良いドアである為には次の二つが重要である。素早くしまる事，しまるときの音が小さい事。）

自動車やバイクのサスペンションも一種のバネ振り子＋ダンパ系であるが，おそらくはやはり臨界減衰に近いような設定が良いのであろうと考えられます，（実際にはより複雑な状況もあり，そこまで単純ではないかも知れませんが。）

強制振動

ここからは強制振動系を考えよう。先の減衰振動系に外から周期的な外力を加える事を考える。

参考：計算数理AのHP

扱う方程式は，以下のようになる。

(3) $\begin{equation*} \frac{d^2y}{dt^2} + 2k\frac{dy}{dt}+\omega^2y=A\cos \omega_e t \end{equation*}$

見ての通り，右辺が０であれば（２）の減衰振動系となります。つまりは，（２）の減衰振動系（放っておけば減衰して静止する）に対して，外から周期的な外力を加えているのが（３）であります。

課題２

（３）を解くプログラムを作成せよ。下の図のように $y(t)$ と $A\cos \omega_e t$ 同時に表示するようにしてください.例えばパラメータ，初期値としては，

(4) $\begin{align*} y'(0) &= 0 \\ y(0) &= 1.0 \end{align*}$

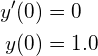
とし，時間刻み幅hはh=0.1とする。解 $y(t)$ を赤色， $A\cos \omega_e t$ を緑色で表示することにする。

A=0の場合（つまり外力が無い場合）には，

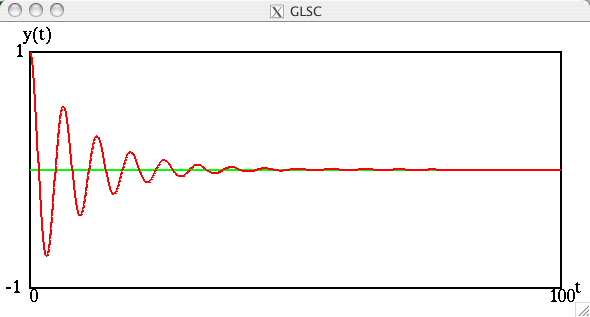
となり，当然ながら減衰振動の様子がみられる。

$A=0.1$ の場合には，

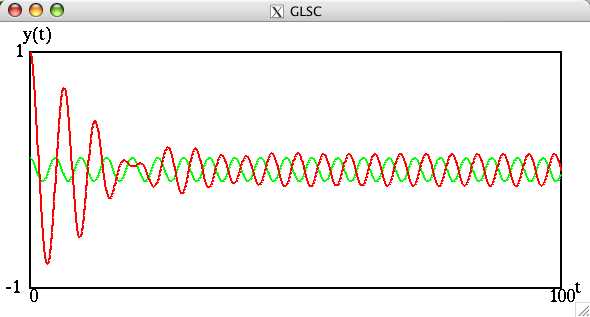
となり，過渡応答，定常応答が見られる。

$A=0.1, \omega_e=1.0$ の場合には，次のようになる。

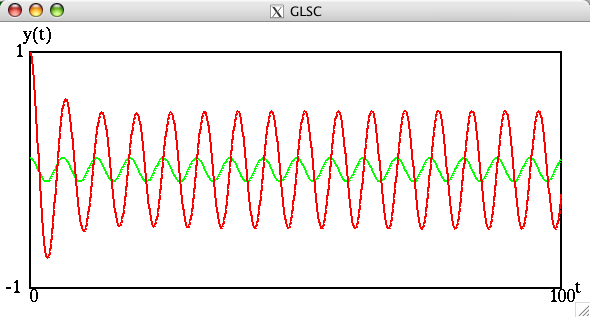
課題3

横軸をyとして，質点の動きをアニメーションで示せ。また，外力の項（ $A\cos \omega_e t$ ）の力の向きと大きさも可視化してください。

参考用動画( $k=0.1, \omega=1.0, \omega_e=1.6, A=0.1$ ）

動画中では，青いバーは $\cos \omega_e t$ を表しており，右側にあるときは右向きに，左側にあるときは左向きに外力がかかっている。

（Aの大きさを青いバーの長さに反映させるかどうかは，各自の判断に任せます。）

課題4

(1) $\omega_e =0.2, 0.4, 0.6, \cdots 2.0$ に対して， $y(t)$ と $A \cos \omega_e t$ の様子（振幅や位相の関係）を見てみよ.

(2)各 $\omega_e$ に対して， $A=0.1, 1.0, 10.0$ とした場合の $y(t)$ と $A \cos \omega_e t$ の様子（振幅や位相の関係）を見てみよ.

(3)横軸 $y$ ，縦軸 $dy/dt$ として表示し，振動の様子を見よ.

(1)(2)から分かるように，バネの固有の振動数ω(外力，抵抗が無いときの振動の周期の逆数)と，外力の振動数ω_eが近くなるにつれ，大きな振幅の振動が現れます。
これが「共鳴（共振）」と言われる現象で，例えばブランコを手で押して大きく揺らす事等は（ふつうブランコの揺れに合わせて押すことで振幅を大きくすると思いますが。），強制振動による共鳴の典型例です。
(逆にこのようなバネ系は，強く揺すってもまあそれ相応にしか振幅はふえません.外からの揺すりの「タイミング」が肝ですね.それを実感してください.)

レポート課題
課題3と同様に強制振動の式（3）を用いて，課題3のようなアニメーション
（t=0から100までのアニメーション，時刻tもwindow内に表示）を表示するプログラムrep20180509.c作成せよ。

ただし、t≧70のときは、
・t=70から現在の時刻tまでの範囲における $y$ の最小値、最大値の位置をそれぞれ縦線で図示すること。
（つまりt=80のときは $70\le t\le 80$ の範囲における $y$ の最小値、最大値の位置を縦線で図示する。）

アニメーション終了後は、また， $70\le t\le 100$ における $y(t)$ の最大値と最小値の差をDとして，そのDの値を画面に表示すること。
ただし，D=1.6（誤差は3パーセントまで許す）となるように $A$ ， $\omega_e$ を設定し， $A$ の値， $\omega_e$ の値はアニメーションのウィンドウ内に表示すること。他のパラメータ（k，ω）、初期値は課題２と同じものとする。

プログラムは関数を用いて，main文が長くなりすぎないように注意してください。
（注意点：質点の運動が画面内に収まるように座標系を設定して下さい.また $\cos \omega_e t$ を表すバーの大きさは見やすいように大きさを調整してくれてかまいません。）
Runge-Kutta法、Eular法のどちらで解いてもかまいませんが、Runge-Kutta法で解いた場合は１割程度高い点をつける予定です。

課題5

バネは大きく伸び縮みすると急激に硬くなるような場合もあります.そのようなバネに対する強制振動系として，次の微分方程式

(5) $\begin{align*} \frac{dy}{dt} &= v \\ \frac{dv}{dt} &= -0.3 v - y^3+B \cos(t) \end{align*}$

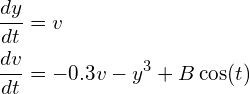
を考えます.この式を数値的に解いて、B=0，1，2，….，12，…，60…等いろいろな場合のyの時間変化を調べてください。特にy，vの初期値が少し違う場合の.yの時間変化を比較してください.課題２，３とどのような特徴の違いがあるでしょうか.（十分大きいtまでの結果を見てみてください.また横軸y，縦軸vとして表示した場合の様子も見てみてください.）

ハードディスクから原子炉まで、様々な機械の「振動」が、このような方程式を応用しながら解析されています.

自然界の振動

上記では，摩擦が働く等して放っておいたら止まってしまうようなシステム(バネ系)が，外部からの「振動（時間に依存して振動的に変化する外力）」を受ける事で定常的に振動する様子について考察しました.しかし実際には，外からの影響が「振動的」でなくても（外力が時間変化しない.つまり方程式の右辺に「t」が現れない.），システム自身が振動的になる場合があります.そのような振動は「自励振動」と呼ばれます。以下，自励振動の簡単な例題を見ていきます.生物を含む自然界の様々な場面で見られるいろいろな「振動（リズム）」の多くが，自励振動であります.（体内時計，脳波，生態系，為替変動，蛇口の水滴，地震，気象，..等等.*宇宙や惑星の運動等は少々違います…）