広島県出身。
2003年3月、広島大学大学院教育学研究科博士課程後期修了。博士（教育学）。

国公立・私立の中学・高等学校にて数学科講師、教諭として勤めた後（～2006年まで）、愛知教育大学教育学部に赴任し、大学教員として算数・数学科教育に携わりました。
2011年より広島大学大学院教育学研究科（現人間社会科学研究科）に籍を移し、現在に至ります。

研究者総覧

図形・幾何に関わる指導と学習に関心があります。
知覚と論理の競合、葛藤、調和がこの研究領域の魅力であり、数学的学びの起こりのリアルに触れることができます。

参考：Kageyama(2013)

たとえば、小学校から中学校にかけて立体の様々な表現方法を学びますが、そこでは奥行きや形状等を捉える具体物の知覚、数学的表現の規則、概念として知っている事柄などの間の調整が暗に求められます。

図．どちらが正四面体でしょうか
４つの面の形や枚数を知っていれば、見え方に惑うことなく答えられるはずです。

八面体や十二面体のように、いつも触れているわけではないが概念として知っているはずの立体のことを問われたとき、知覚主体（～のようにみえてしまう; perceiving）か概念主体（～のようにみえるはずだ; conceiving）かによってアプローチはかわることでしょう。皆が皆、同じアプローチをとるわけではないし、それぞれに一定の理があるはずです。たとえカリキュラムによって内容が決められていようとも、それを通して起こる学びまで制御することには謙虚でありたいと考えます。

近年では、特殊な空間である≪教室≫に注目して、皆が共にいるからこそ起こる、
● 学びたいこと
● まだここにないこと
に取り組みたいという≪衝動≫の重要性に注目しています。これらは往々にして、集団サイズとしてのミクロ・メゾ・マクロの関わりによって起こり（創発）、翻ってそれが運動を自己規定していきます（設計）。

影山和也（2019）. 数学教育における学習作業空間論に関する総合的研究. 「数学教育学研究」,vol.25(2), 91-100.

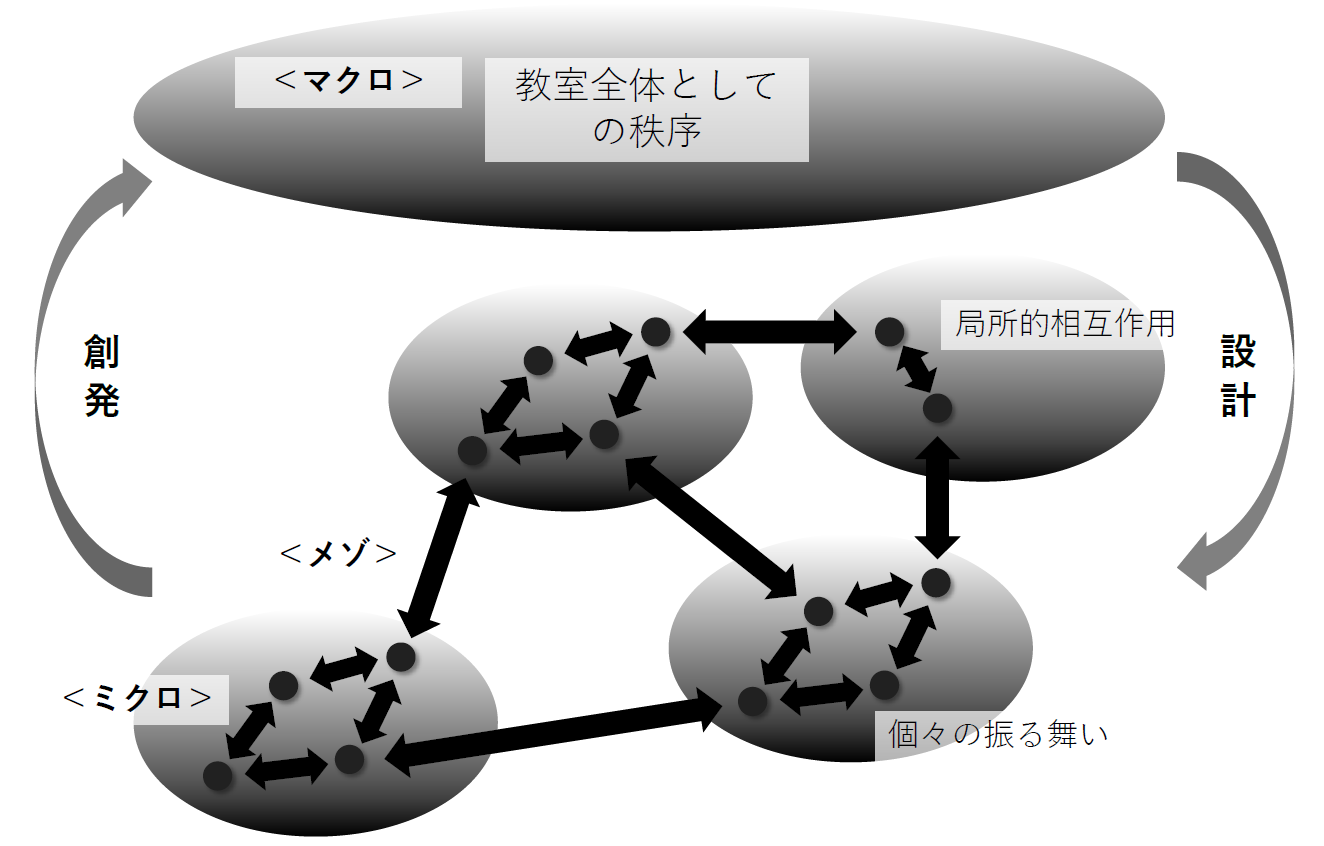
図．教室での関わり合いのイメージ（影山（2019）より：図５の一部改編）

ミクロ・メゾ・マクロは知識や技能の起こりを説明するスケール・モデルですが、その背景には、サイズが違えば人と人の関わり方が違い、互いの配慮関係もまた異質になるという事実があります。ミクロであれば目の前に居る他者に対して直接の配慮をしやすいですが（care for）、メゾ・マクロと公共性が増すにつれて、すべての活動に関与していなくても他者を気にかける（care about）という関係性が生まれます。重要な点は、互いに支え合うという関係の編み目のなかに自己があるという認識であり、その関わり合いのために自らの力量を高めねばならないという自省です。 (2023.01.25追記)

Varela, Thompson, & Rosch(2017). The Embodied mind: cognitive science and human experience. MIT Press(revised ver.).

Davis & Sumara(2008). Complexity as a theory of education, Transnational Curriculum Inquiry, 5(2), 33-44.

このような発想はH.Maturana & F.Varelaによる現成主義（enactivism）（Varela et al.,2017）、身体論哲学、複雑性科学、さらにはケアリングの思想に由来します。人のリアルを加味し、暗黙の前提を疑い、既存の領域を越境しようという試みは決して新しいものではありませんが（Davis & Sumara, 2008）、あらかじめ単元や教科によって準備された道筋を辿るのではない仕方で、そして他者との関係性開発と維持のために、数学の指導と学習を考えることには大きな可能性があると思います。

エナクティヴ・アプローチには次の二つのポイントがある：
(1)生物の知覚は、知覚的にガイドされた行為からなる
(2)認知構造は再帰的な感覚運動パターンから創発し、それによって行為は知覚的にガイドされる
こうして、知覚、知ること、考えることと行為とは一体であると見なされる。

Florial, L. (2013). The SAGE Handbook of Special Education. SAGE Publication (second edition.).

「すべての人のための数学」（mathematics for all）の理念は、およそ40年前にユネスコによって公的に提唱されました。その後、あらゆる方面で連動し、「障害」（disability）についての捉え方も医療モデルから社会モデルとその先へと変容し、インクルージョンの概念が理念上も政治上も実践上も普及しつつある現代（Florian, L. (Ed.), 2013）、「すべての人のための理数教育」（mathematics and science education for all）が教育研究として希求されています。現代の研究において、倫理や責任の問題が欠かせないように、すべての人たちがそれぞれのニーズと仕方とで理数に関わるための基盤づくりが当面の使命です。