確率・統計B

Modified : 04/13/12 15:07

お知らせ

レポートの再提出について
2/1(水)にレポートを返却しました。
欠席した人は、数学事務室のカウンター前の返却ボックスから各自持って行ってください。
表紙に赤字で問題番号が書いてありますが、その解答の修正が必要です。
その部分の解答を作成して、２月９日(木)までに、数学事務室の指定ボックスに再提出してください。
2/1の講義の最後に, 駆け足で説明した練習問題２問１の解法に一部誤りがありました。練習問題２問１の解法(pdfファイル)で確認してください.
練習問題２の問３を一部修正しています。(講義で指摘があった部分）
期末試験情報を更新しました.
中間試験以降の講義内容に関する練習問題２(pdfファイル)を作成しました。
レポート問題の解答を掲載しています。解法は正しいはずですが, ひょっとすると計算ミスがあるかも知れません。気がついたら教えてください。期末試験に向けて, 分からなかった問題をチェックしておいてください。
2月8日に期末試験を行います。
レポート提出について
12/7の講義のときに, 中間試験の答案を返却しました。
40点未満の人は, レポートとして練習問題(pdfファイル) と中間試験問題(pdfファイル) の完璧な解答を作成して
１２月２２日（木）までに
数学事務室カウンター前のボックスに
提出してください。 12/21の講義のときに、直接手渡しで提出してもかまいません。なお、このお知らせは授業掲示板にも掲載されており, 掲示にある添付ファイルと, 上記のファイルは同じものです。
統計分野卒業研究ゼミの見学
講義とは直接関係ありませんが, 来年度の卒業研究で統計分野(私と柳原先生のゼミ）を考えている人を対象に次のゼミを公開しています.
日時: 12月13日(火), 14:35-
場所: C816
興味のある人は見学に来てください。
11月30日に中間試験を行います。

期末試験

日時：２月８日(水), 10:30-12:00
場所：いつもの講義室
試験範囲：講義した内容について出題します。講義記録を参考にしてください。テキストでは、第５章、第６章(6.3節まで), 第７章(7.1節と7.3節), 第８章(8.1節と8.2節)です。 8.2節の不偏検定は試験範囲に入れません。）

中間試験の範囲については、中間試験問題と練習問題によく似た問題を出します。レポートの解答を参考にしてください。
中間試験以降の範囲については、練習問題２(pdfファイル)を参考にしてください。テキストの演習問題なども参考にして準備してください。

中間試験

日時：11月30日(水), 10:30-11:30 (答案提出後, 試験問題の解説などの授業)
場所：いつもの講義室
試験範囲：テキストの第5章, 第6章(定理6.5まで)

練習問題(pdfファイル)のような問題を出します. 試験時間は1時間なので、量は半分くらいです. テキスト章末の演習問題も解いてみると良いです.

テキスト

「確率・統計の基礎」藤越・若木・栁原著
(参考書：「確率論」西尾真喜子著)

質問と回答

Q: $P(A\cup B)=P(A)+P(B)-P(A\cap B)$ の証明は, ベン図を使用して共通部分のない集合で表すしかないのですか.
A: 有限加法性を用いるこの方法が標準的で, 私も他の方法を知りません.
Q: べき集合をσ-集合体とすると起こりうる都合の悪いこととは何ですか
A: 宝くじの抽選のように, 回転させた円盤に矢を放って基準線から矢がささった所までの角度を測定するという実験を行うときは, どの角度も同様に確からしいと考えられるので, 例えば, 30度から50度の間に矢がささる確率と, 70度から90度の間に矢がささる確率は同じになるような確率を定義することになります. このような回転に関して不変な確率の定義域として, べき集合をとると矛盾が生じることが証明できます.
Q: 確率・統計Aの単位を落としていて, 復習をしようと思いますが、どのように勉強すれば良いですか.
A: テキストやノートの定義や基本的な定理の証明を納得できるまで繰り返し読む, 演習問題を解く, 分からないところは誰かに質問する, というのが私が学生の時の勉強法です. まずは, 確率・統計Aの中間試験や期末試験, 演習の問題などをもう一度解いてみて, どこが分かっていないのか確認してみてはどうでしょうか.
難しすぎて何が何か分かりません. 履修するかどうか悩んでます.
A: 履修するなら, まずは, 下の講義記録(10/05)にある言葉の定義をテキストから探して, そこに書いてある説明や例を読み, 定義から導かれる基本的な性質を確認してください.
少しスピードが速いです. もう少しゆっくりしてください.
A: 講義でも言いましたが, 講義したい内容の量を考えるとスピードは速めになると思います。テキストを事前に読んでおいて, 分からない部分を講義で確認するというようにすると良いです.
Q: $\forall k,\omega\in\bigcup_{m=1}^{\infty}\bigcap_{n=m}^{\infty}A_{n}(\frac{1}{k})$ と $\omega\in\bigcap_{k=1}^{\infty}\bigcup_{m=1}^{\infty}\bigcap_{n=m}^{\infty}A_{n}(\frac{1}{k})$ は同じ意味ですか.
A: 同じ意味です. 集合列 $\{A_k\}$ があるとき, その積集合は $\bigcap_{k=1}^{\infty} A_k=\{\omega;\forall k,\omega\in A_k\}$ によって定義されます.
Q: (11/2 の講義で) 板書にあった「 $\Rightarrow P(|X_{n}|\ge M_{k})\ge 1-\eps$ 」の最初の不等号は反対ではないですか。
A: ご指摘の通り書き間違いです. 「 $\Rightarrow P(|X_{n}|\le M_{k})\ge 1-\eps$ 」が正しいです。
Q: 実現値とは, 母集団Ωからωを無作為抽出したときのX(ω)のことでしょうか。
A: その通りです. 例えば, 1万人の子供の母集団から無作為抽出して身長Xを測定する場合, ωは各子供を表し, X(ω)は抽出された子供の身長を表します.
Q: $\frac{1}{n}\sum_{i=1}^{n}X_{i}^{2}-\bar{X}_{n}^{2}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\bar{X}_{n})^{2}$ の式変形をどうするのでしょうか?
A: $E(X^*)=\bar{X}_{n}$ なので, 分散の公式 $Var(X^*)=E[(X^*)^2] - \{E(X^*)\}^2$ を当てはめれば良いです. 具体的には, 右辺を展開して, 添え字 i がついていない項を $\sum_{i=1}^n$ の外に出せばできます.
Q: 少しとんちんかんなことを質問するかも知れませんが, 母集団が無限個のときは AC を認めるということですか?
A: AC が何のことか確信が持てませんが, 選択公理のことだとすると, 「無限集合から要素を取り出す」ということと選択公理を認めるかどうかとは別のことです. 選択公理は, 「無限集合族の要素である各集合から, その元をひとつづつ取り出すことが可能」というものです. 無限母集団からどうやって同じ確からしさで対象を抽出するかという疑問からの質問ではないかと思いますが, 実は,「同じ確からしさ」ということばで直感に訴えているだけで, 厳密に定義していないのです. 下の回答を参考にしてください.
Q: (母集団が有限のとき)無作為抽出を確率空間を使って説明するとどうなるか考えたのですが,
$\Omega$ を標本空間(母集団), $\mathcal{B}=\sigma(\{\{\omega\}|\omega\in\Omega\})$ , $(\Omega,\mathcal{B})$ 上の確率 $P$ を $P(\{\omega\})=p$ からなる確率空間上で確率変数や分布関数を考えているということで合っていますか?
A: 合っています. ただし, $\Omega$ の要素数を $N$ とすると, $p=1/N$ です.
無限母集団に対して数学的に厳密に無作為抽出を定義するのは, 実は無理があります. 母集団が閉区間 $\Omega=[a,b]$ の場合には, $\mathcal{B}$ を $\Omega$ に含まれるボレル集合の全体として, $P$ は $[a,b]$ 上の一様分布とすれば, どの点も同じ確からしさで選択するといってよいと思いますが, 例えば母集団が有理数の全体の場合, 「同じ確からしさで選択する」というときの確からしさを確率測度として定義することはできません. 無限母集団に対しては, 定義6.3(標本と母集団分布の数学的な定義) を出発点と考えてください.
11/16の講義の後半はスピードが速すぎてノートを取れなかったという意見がありました. 申し訳ありません. 復習に時間を使いすぎてしまいました. 定理6.5 を証明して, その特別な場合というつもりだったので, 定理6.4 の証明は時間をかけないという意識があったためでもあります. テキストの証明を読んで, 分からなければ質問に来てください.
Q: 定理6.8の中の $\frac{1}{\sqrt{n}}\mathbb{1}_n'$ は $\frac{1}{\sqrt{n}}$ 倍の $\mathbb{1}_n'$ ということですよね.
A: そうです.
Q: 統計モデルは同じ種類の分布を集めたものなのでしょうか？それとも違う種類のものや余計なものが入っていてもよいのでしょうか？
A: 統計モデルは, 母集団分布の候補となるものを集めたものなので, 通常は同じ種類です. 余計なものが入っていては困るのですが, 入ってしまうということはあります. 例えば、群生しているある植物の分布を調査しようとしているときに, 想定している種とは異なる種の植物が混ざっている場合などです。調査の過程で、異なる種の植物が一定の割合で含まれることに気づけば、それを考慮したより広い統計モデルを設定して調査を進めることになりますが, こうなると異なる種は、余計なものとは呼ばず、その割合も母集団の特性値と考えることになります。余計なものが多少含まれても、分析結果がそれほど大きく変わらないようにするための統計的手法も研究されています。
Q:「確率統計の数学的基礎」で標本メジアンの定義が 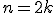$n=2k$ のとき, $\bar{X}=(Y_k+Y_{k+1})$ と書かれていますが, これは $\bar{X}=\frac{(Y_k+Y_{k+1})}{2}$ が正しいのですか.
A:そうです. テキストが間違っています.
Q: 定理6.8 (3) $\bar{X}_n$ と $S_n^2$ は独立と板書にあり, テキストでは「 $\bar{X}_n$ と $S_n^$ は独立」とありますが, どちらでもいいのでしょうか？
A:どちらでも良いです. 独立であるための必要十分条件が「同時確率密度関数が周辺確率密度関数の積になる」ということを使えば両者が同値であることが証明できます.
Q:100α％調整平均の例で, 板書の意味がよくわかりません。
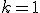A:テキスト128ページで, $n=5,\alpha=0.2$ とすると, $k=1$ となり, 20％調整平均は $\frac{1}{3}(Y_2+Y_3+Y_4)$ となります. 板書で $\frac{2}{5}=0.4$ 40 と書いたのは, テキストの(4)式では, 大きいほうと小さいほうをそれぞれ, 100αパーセント削除した残りの平均値を計算しており, 例では, 大きいほうと小さいほうを合わせて 40％削除しているので, 40÷2=20 なので, 20％調整平均と書きました.
Q: $\hat{\gamma}(\mathbb{X})$ は $\theta$ に依らないのですか?
A: $\hat{\gamma}(\mathbb{X})$ は $\theta$ は依存しないものです. 本来, $\theta$ の値が分からないから $\gamma(\theta)$ を推定するので, $\hat{\gamma}(\mathbb{X})$ が $\theta$ に依存してしまうと, 推定に使えなくなってしまいます.
関数 $\hat{\gamma}(\mathbb{x})$ が $\theta$ に依存するかどうかと, 推定量 $\hat{\gamma}(\mathbb{X})$ の分布が $\theta$ に依存するかどうかを区別してください. ここで言う $\theta$ に依存しないというのは, $\mathbb{X}$ の実現値, $\mathbb{x}$ の値が決まれば, 推定値 $\hat{\gamma}(\mathbb{x})$ も決まるという意味です. 確率ベクトル $\mathbb{X}$ の分布は, $\theta$ に依存しているので, 推定量 $\hat{\gamma}(\mathbb{X})$ の分布は $\theta$ に依存しています.
Q: レポートは返却されるのでしょうか.
A: 返却しますが、もうしばらく待ってください。
Q: 正規分布の例で, なぜ $\gamma(\theta)=\theta$ ならば $\{\gamma(\theta)\}^2=1$ となるのですか。
A: $\{\gamma(\theta)\}^2=1$ ではなくて, $\{\gamma'(\theta)\}^2=1$ です。
Q: $\mathbb{X}\sim P_\theta\in\mathscr{P}=\{P_\theta |\cdots$ と書く場合と, $\mathbb{X}\sim P\in\mathscr{P}=\{P_\theta |\cdots$ と書く場合がありますが, 意味があって使い分けていますか.
A:統計モデル( $\mathscr{P}$ のこと)を意識し, $P\in\mathscr{P}=$ と書くことで, 母集団分布 $P$ が統計モデルに含まれるというのは仮定であり、実際に成り立つとは限らないという意味合いで, 後者を書こうと思っているのですが、普段は $\mathbb{X}\sim P_\theta, \theta\in\Theta$ と省略するので、うっかり書いてしまいます。前者も後者も同じ意味で、母数が未知と既知を区別しているのではありません。
Q:クラメール－ラオの不等式と十分統計量の関係をもう一度説明してください。
A:クラメール－ラオの不等式は、不偏推定量の分散の下限（一般的な用語として下限と言っていますが、数学的に厳密に言うなら下界のひとつ）を与えるものです。十分統計量は、不偏推定量が与えられたとき、それと同等以上（分散が等しいか小さい）の不偏推定量を得るために使える統計量です（ラオ－ブラックウェルの定理）。有効推定量であれば、一様最小分散不偏推定量であるが、逆は必ずしも成立しません。完備十分統計量の関数として不偏推定量が与えられれば、一様最小分散不偏推定量であるので、その分散とクラメールーラオの下限を比較することで、有効推定量が存在するかどうかがわかります。
Q:不偏推定量や統計量の具体例やどのような場面で使われているかについて参考書でも良いので教えてください。
A:具体例としては、講義でも紹介した標本平均や標本分散、また、先端数学で解説した、偏回帰係数の最小２乗推定量などは不偏推定量の例です。実社会でどのように使われるかについては、臨床試験や品質管理などの例を講義で示したと思います。参考書は思いつきませんが、臨床試験や品質管理、あるいは、生物統計などに関する書籍を探せば、その中でどのような統計量が使われるかが書かれていると思います。科学実験の結果を論文にまとめるときは必ず実験データを用いて仮説検定や推定などが行われますので、他学科の人に聞いてみると、実用例を見せてもらえるかも知れません。今年の数理統計学グループの卒業研究では、4人がデータ解析を行っているので、卒論発表会で実践例を聞くことができます。

講義記録

10/05
確率・統計Aの復習
確率空間, 確率変数(1次元, 多次元, 独立性), 確率分布(離散型, 連続型), 期待値, 特性関数
第５章確率変数と分布の収束
10/12
分布収束の定義, 分布収束と確率収束の関係, 例
宿題「定理5.2 を証明せよ.」(提出しなくてよい)
10/19
中心極限定理, 連続性の補正, 概収束の定義と必要十分条件(必要性の証明まで)
10/26
概収束の必要十分条件, 概収束 ⇒ 確率収束, 漸近公式, スラスキーの定理（証明はまだ）
11/02
スラスキーの定理の証明, 確率ベクトルの収束（概収束, 確率収束, 分布収束）
11/09
第６章標本分布
母集団と標本(有限母集団,　無限母集団,　無作為抽出, 復元抽出, 非復元抽出)
母集団分布, 無作為標本(確率変数と実現値), 統計モデル
経験分布関数, 経験分布関数の確率変数としての性質
11/16
統計量の定義, 標本平均と標本分散の性質(定理6.2, 定理6.3), 正規母集団からの統計量(1次式)の分布(定理6.5, 定理6.4)
統計量の分布の求め方(特性関数を調べる方法, 変数変換による方法)
11/30
中間試験(65分), 試験問題の解説
12/7
統計量の分布（カイ2乗分布）
12/14
統計量の分布(カイ2乗分布, F分布, t分布), 順序統計量
第７章推定
点推定, 推定値, 推定量
12/21
推定量の良さの基準(偏り, 平均２乗誤差, 分散, 集中確率, 一致性, 不偏性)
一様最小分散不偏推定量(クラメール－ラオの不等式, 有効推定量)
(テキスト 7.2節は飛ばした)
1/11
一様最小分散不偏推定量(十分統計量, ラオ－ブラックウェルの定理, 分解定理, 完備性)
例. 正規母集団の母平均の推定(クラメール－ラオ不等式の導出と標本平均）
例. 正規分布の母数の十分統計量
1/18
第８章仮説検定
仮説検定の考え方と用語(帰無仮説、対立仮説、棄却、第１種・第２種の過誤、危険率、優位水準）例（新薬の効果）
1/25
、ネイマン－ピアソンの補題、一様最強力検定、例（正規母集団の母平均に関する検定）
2/1
中間試験以降の復習(練習問題２(pdfファイル))の解説。
期末試験について。