量子化学を初めて勉強する方のページ
こんにちは、阿部穣里です。このHPは2020年以前に阿部が東京農工大で化学基礎を講義させていただいたときの情報がまとめてあります。現在阿部は広島大学に所属しており、この内容の講義はしていないのでご注意ください。どなたかの参考にと思って残しております。
======
上のリンクをクリックしてみてください。
いろんな問題が複雑にからんでいますが、
量子化学のエッセンスはたかだか2ページにまとめられてしまいます。
このマインドマップがフムフムとわかればOK!そのために一つずつ勉強していきましょう。
最初は難解でちんぷんかんぷんかもしれません。
先生の教え方が悪いのだと思うかもしれません。(すいません…)
しかし、2,3回類似の講義を聞いて、課題を解き単位を取り、研究室に配属され勉強会をして、卒研をやってみて、なんならTAでもやって1年生に指導でもすれば
誰でも、量子化学はわかるようになります。要は慣れ(というか反復)です。私が量子化学を専門にできているのも、上記のプロセスを経たにすぎません。
イントロダクション動画
を必ず見てから受講をご判断ください.(PDF版はこちら)
オンライン講義の進め方
1. 毎回、冒頭は小テストの演習時間があります.(成績に含みます)
2. 小テストの解説はYoutubeなどで用意してありますので、必ず事前に予習をしてから参加してください.
3.小テスト3回以上の欠席で単位を認定しません。
3. 講義の後半は、講師から説明をします. 穴埋め式の講義資料は事前に印刷しておいて書き込まれることを推奨します。(タッチペンでもOK)
4. レポートが3回あります. 小テストとレポートで成績を付けます。
5.初回のレポートはすぐ提出です(5月15日 5月17日に変更しました)。準備をお忘れなく。
6.なので5月13日までには、小テストの準備+レポートの問題も進めておく必要があります!
講義計画 (注:コロナでオンラインの時の計画)
|
|
小テスト(30分) |
講義(60分) |
|
レポート |
|
0 |
第0回演習問題(宿題) 解説動画(人)(1.運動方程式、 2.エネルギー保存則、 3.運動量保存則、4.等速円運動、5.6.等速円運動続き(エネルギー) 解説動画(AI)(1.運動方程式、 2.エネルギー保存則、 3.運動量保存則、4.等速円運動、5.6.等速円運動続き(エネルギー) 静止画解答(電子版(略解2-6)、4-1,4-2,4-3,5,6)
|
|
|
|
|
1 |
角運動量・ボーアモデルの角運動量 (ヒントの解説資料 第1回問題 第1回動画(人)(7.角運動量、8.ボーアモデルの計算) 第1回動画(AI)(7.角運動量、8.ボーアモデルの計算) 第1回静止画解答(7-1,7-2,8-1,8-2, 電子版(略解))
|
ボーアモデル (課題1) オンライン講義資料(New)
偏微分の解説
|
5月13日 |
|
|
2 |
波動 第2回動画(AI) (9.波動) 第2回静止画解答(9-1,9-2,3,9-4,電子版(略解))
|
物質、光 |
5月20日 |
|
|
3 |
演算子・固有値・固有関数・極座標 第3回問題 第3回動画(人) (10.演算子・固有値・固有関数の①、②、③、④、⑤、⑥ 11.極座標、(参考・補足)極座標の微小体積 ) 第3回動画(AI) (10.演算子・固有値・固有関数の①、②、③、④、⑤、⑥ 11.極座標 第3回静止画解答(10-①,10-②③、10-④、10-⑤、
|
シュレディンガー方程式導出
波動関数の性質 |
5月27日 |
|
|
4 |
シュレディンガー方程式 波動関数の性質 第4回問題 第4回動画(人) (12.シュレディンガー方程式の導出 13.波動関数の性質) 第4回動画(AI) (12.シュレディンガー方程式の導出 13.波動関数の性質)
|
1次元井戸型ポテンシャル |
6月3日 |
|
|
5 |
1次元井戸型ポテンシャル 第5回問題 第5回動画(人) (14.1次元井戸型ポテンシャル) 第5回動画(AI) (14.1次元井戸型ポテンシャル)
|
2,3次元井戸型ポテンシャル |
6月
10日 |
|
|
6 |
休み |
水素原子のシュレディンガー方程式の
|
6月
17日 |
レポート② |
|
7 |
水素原子のシュレディンガーの解 第7回問題 第7回動画 (人) (15.水素原子の解1s軌道のエネルギー ) 第7回動画(AI) (15.水素原子の解1s軌道のエネルギー ) 問題16については配布資料を参照せよ
|
6月24日 |
|
|
|
8 |
ラプラシアンについて
原子軌道 第8回動画 (AI) (17.ラプラシアン )
|
多電子原子、電子配置、スピン |
7月1日 |
|
|
9 |
多電子原子・電子配置・スピン
|
H2+分子のハミルトニアン
LCAO (原子軌道で線形結合とる近似) |
7月8日 |
|
|
10 |
H2+分子,
LCAO近似 第10回問題 第10回動画(AI)(H2+分子 その1(ハミルトニアン)、その2(変分原理、LCAO)、 第10回 電子版(略解)
|
振り返り 分子軌道と化学反応 自由研究に関する参考: PC Chemウェブサイト(おすすめ) WebMOの使い方 Gamessをクラウド上で計算させる方法
Maximaインストールから使い方まで |
7月15日 |
|
| レポート③ | ||||
|
レポートが未提出の場合、単位がありません。 締め切りに遅れた場合、大幅な減点があります。
レポート① 締め切り5月17日(24時) ・第0回の課題を全て解いて提出。(写真かPDFをClassroomからアップロードの予定)
レポート② 締め切り6月17日 ・第1回から第4回の内容(シュレディンガー方程式の導出、波動関数の性質)を復習し、自分の頭で様々な内容の関連性を編集し、自分の言葉でアウトプットする。小テストだけでなく、講義で扱った内容をしっかり含めること。
参考書もはじめから読んでみよう。既に数学的なところは一度手を動かしているので、思いのほかよくわかると思います。初日に配ったマインドマップも参考に。
レポート③ 締め切り 7月29日(予定)
第5回(井戸型ポテンシャル)から第10回までの内容を復習し、
|
Dr. Quantumの電子2重スリット問題に関するyoutube動画はこちら!
このページでは化学基礎、量子化学入門、構造化学など、初めて大学で理論化学を学ぶ方に向けた情報を発信したいと思っています。
大学で学ぶ化学の基礎には、ずばり、高校で勉強した物理や数学がたくさん潜んでいます。
高校の数学で、なぜ微分積分が出てきたのか、なぜ複素数が出てきたのか?
なぜ確率統計が出てきたのか、なぜ三角関数が出てきたのか?
なぜeとかlogがでてきたのか、なぜ数列を勉強したのか?
なぜ線形代数、ベクトル、行列を勉強したのか?
皆さんが学んだ高校の数学の内容は、実は大学で学ぶ科学全般でとっても必要なのです。
それは数学とは関係なさそうな化学にさえもなのです!
上に書いた高校数学の概念が、実際すべて化学基礎で用いられています。
ついに高校数学が、役に立つときが来ましたよ。苦手だった単元はこれを機に復習できるといいですね。
また物理ですが、ニュートンの考えたF=maの式が、化学基礎にはふんだんに出てきます。
しかしながらF=maだけではどうしても説明できない現象が、電子のような小さい物質には現れてしまいます。
昔の科学者は何とかして、このF=maの進化形を考えて、電子のような小さな物質のための法則を考えました。
そして行きつく先がシュレディンガー方程式なのです。
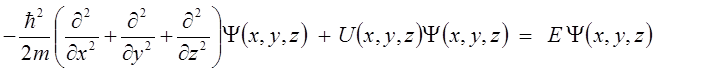
ぎょわー、なんじゃこりゃ!と思われるかもしれませんが、大丈夫です。見慣れればなんてことはありません。
大学で化学を考える時には、この化学の根底にあるシュレディンガー方程式などの基礎理論を理解していると色々なことが理解できます。
s軌道、p軌道、d軌道はなんなのか?どこからでてくるのか?
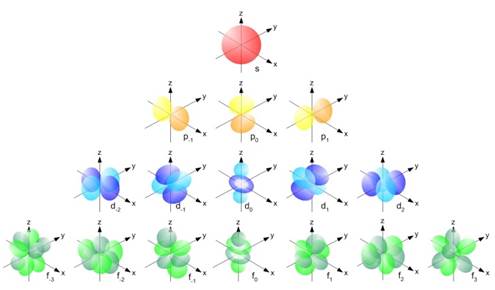
(chemwikiより)
化学結合とはなんなのか?手が8本??いえいえ、大学の化学では高校で学んだものとは異なるとらえ方をします。
また、この量子化学を理解していると、コンピュータと頭があれば、化学を議論することが可能です。
プログラムを書けば、お金儲けも社会貢献も可能になります。
まだできていない分子を予想することも可能でしょう。